Bagan - Chetabahana/method GitHub Wiki

	This wiki is courtesy of Chetabahana Project. Find all of them on Project Map.
⏫	🔼	⏪ Intro	◀️ Prev	🔁 Repo	Next ▶️	Last ⏩	🔽	⏬

Bagan adalah sebuah representasi grafis dari data. Data yang diwakili dibentuk oleh simbol-simbol, seperti batang dalam bagan batang, bagan garis, atau irisan dalam bagan pai.

Dari ke tujuh (7) kasus Millenium Prize Problems yang dipublikasikan sejak tahun 2000 dalam rangka menyongsong abad milenial, satu kasus yaitu Poincaré conjecture sudah dipecahkan.

Solusinya diakui pada tahun 2010. Jadi satu kasus saja makan waktu 10 tahun. Entah sisanya kapan bisa dipecahkan.

Seperti kata pepatah, tidak ada ruginya untuk coba paham, minimal kita tahu bahwa ada kasus semacam ini.

Maka saya temukan korelasinya dengan Sistem DNA. Padahal Kasus Milenial ini sudah lama dipulikasikan. Pengetahuan tentang Sistem DNA juga entah dari kapan sudah ditemukan.

Metode saya sederhana saja, Anda juga bisa ikuti caranya:

• Kumpulkan semua referensi yang bisa Anda dapat sampai tak bersisa lagi,
• Temukan dan tulis apapun yang Anda anggap penting dari semua referensi itu,
• Susun sedemikian rupa sehingga nyambung satu sama lain fokus ke satu hal saja.

Dia sambungin antara yang program penelitian yang ditemukan Richard Hamilton dengan Ricci flow yang pada akhirnya menghasilkan bukti .

Itu juga sebabnya dia tolak hadiah yang $1 juta. Karena dia anggap kontribusinya cuma sebatas nyambung²in tadi. Simak pernyataannya yang dikutip Wikipedia:

• Kantor berita Interfaz mewawancarai Perelman yang mengatakan bahwa ia yakin penghargaan itu tidak adil.
• Ia menganggap kontribusinya untuk memecahkan Konjektur Poincare tidak lebih besar dari matematikawan Universitas Columbia, Richard Hamilton.

Mana yang lebih besar kontribusinya, sang penemu atau sang penyambung?

Anda bisa ikuti di Dunia Internet cerita tentang ilmuwan yang penemuannya sangat istimewa yaitu: Isaac Newton dan Albert Einstein.

Dalam sejarahnya mereka mengembangkan penemuan dengan mengambil dasar dari penelitian ilmuwan lain, bahkan pernah dituduh menjiplak ilmu yang ditemukan orang lain.

• Dalam buku catatan Leibniz, dapat ditemukan adanya gagasan-gagasan sistematis yang memperlihatkan bagaimana Leibniz mengembangkan kalkulusnya dari awal sampai akhir, manakala pada catatan Newton hanya dapat ditemukan hasil akhirnya saja. Newton mengklaim bahwa ia enggan mempublikasi kalkulusnya karena takut ditertawakan. Royal Society kemudian dalam suatu kajian memutuskan bahwa Newtonlah penemu sebenarnya dan mencap Leibniz sebagai penjiplak. Kajian ini kemudian diragukan karena setelahnya ditemukan bahwa Newton sendiri yang menulis kata akhir kesimpulan laporan kajian ini.
• Dalam makalahnya mengenai kesetaraan massa-energi, Einstein menciptakan rumus E = mc2 sebagai konsekuensi dari persamaan relativitas khusus. Karya Einstein tahun 1905 tentang relativitas diperdebatkan selama bertahun-tahun, tetapi perlahan diterima oleh para fisikawan terkemuka, yang dimulai dengan Max Planck. Einstein awalnya membingkai relativitas khusus dalam kajian kinematika (ilmu tentang benda bergerak). Pada tahun 1908, Hermann Minkowski menafsirkan ulang relativitas khusus dalam kajian geometris sebagai teori ruang waktu. Einstein menggunakan konsep Minkowski dalam mengembangkan teori relativitas umum pada tahun 1915.

Jadi sebenarnya mereka tidak sepenuhnya menemukan tapi juga nyambungin² sehingga ketemu solusi. Tapi keduanya gak ambil pusing masalah ini dan bersedia terima penghargaan².

Maka disini saya melihat kesalahan Perelman jika menggangap hal itu tidak adil.

Tapi kenapa ya. Kok mereka sang penyambung² ini yang malah diakui dunia?
Jawabannya adalah karena sang penemu dan sang penyambung itu beda.

Prinsipnya suatu ilmu yang ditemukan akan tetap hanya jadi pustaka atau dugaan yang terdengar saja sampai ada yang bisa nyambungin dengan penerapan yang bisa diterima.

Nah di Project ini sebagian besar itu yang saya lakukan, cuma sambung²in dari referensi yang saya dapat. Tapi hasilnya? Saya temukan banyak hal yang tak seorangpun dapat. Ya kan?

Dengan demikian kita akan lakukan metoda sambung menyambung ini dimulai dengan kasus yang sudah dipecahkan yaitu Poincare Conjecture.

Silahkan ikuti selanjutnya..

Sesuai dengan penjelasan di atas, sebelum kita masuk ke tahapan proses maka hal yang pertama dilakukan adalah menerapkan angka pada subjek agar "berkaitan" dengan kelompok pertama.

Hal ini terlenuhi dengan cara menempatkan kasus geometri di kelompok pertama sehingga subjek terkait dengan dua (2) kasus pertama ibarat ada di satu (1) jangkar dengan tiga (3) kaitan.

Prosesnya kita akan lakukan dengan mengadopsi bentuk tetraktis yaitu segitiga karakter seratus dua (102) memiliki dua (2) angka yang membentuknya berupa 10 node dan angka 2 itu sendiri.

Karena angka dua (2) sudah dialokasikan di repository dari organisasi maka kita cari property berupa angka sepuluh (10) pada objek yang 7®.

Ternyata dia ada di urutan pertama dan posisinya di "true prime pairs" tepat di indeks ke-3. Dia ada di jangkar (10,11,12). Berarti angka 10 untuk subjek, dan 11,12 kasus ke-1 dan ke-2.

7® = 5® + 2® = (10,11,12,14,15), (26,28)

True Prime Pairs:
(5,7), (11,13), (17,19)

layer|  i  |   f
-----+-----+------
     |  1  | (2,3)
  1  +-----+
     |  2  | (7)
-----+-----+------
     |  3  | (10,11,12)  <---- {10'} = subject of the taken cases
  2  +-----+
     |  4  | (13)
-----+-----+------
     |  5  | (14,15)
  3  +-----+
     |  6  | (19)
-----+-----+------

Pergeseran ke 11' ini menyisakan Kesenjangan (Gap) di Mid Zone sehingga menyediakan ruang bagi sistem untuk memulai proses berulang via karakter bilateral dari angka sembilan (9).

• Integrate different sources of 'omics data' in environmental science

Tujuannya adalah untuk mendapatkan metode yang sekiranya dapat diimplementasikan sebagai modul terhadap kasus lain berdasarkan suatu kaitan yang dapat dimanfaatkan.

Di pustaka ini Anda juga bisa telusuri solusi untuk salah satu kasus yang sudah dipecahkan, silahkan masukan input dengan nama kunci Grisha Perelman:

Jika kita pelajari kasus² ini jelas merupakan perkara yang extra rumit. Jika Anda memang punya bakat matematika sedari kecil tentu lebih mudah untuk paham.

Namun disini bakat saja tidak akan cukup karena begitu banyak sudah makalah diajukan dari berbagai sumber namun sudah sekian puluh tahun berlalu belum ada yang lain berhasil mengajukan bukti dari solusi.

• Poincaré Conjecture - Cantor's Paradays

"If God speaks to man, he undoubtedly uses the language of mathematics."
(Henri Poincaré)

• Poincaré Conjecture and Homotopy - Lê Nguyên Hoang

• Manifolds with Density and Perelman’s Proof of the Poincaré Conjecture

Poincaré Conjecture, yang disarankan oleh Henri Poincaré pada tahun 1904, mengusulkan hasil analog untuk manifold tiga dimensi: manifold kompak tiga dimensi yang terhubung sederhana harus berupa bola .

Pada Kongres Internasional Matematika 2006, Grigori Perelman dianugerahi Medali Fields untuk buktinya, meskipun ia menolak untuk menerimanya.

Versi dimensi tinggi dari Poincaré Conjecture, dengan lebih banyak ruang untuk melakukan konstruksi geometris, lebih mudah. Stephen Smale membuktikan dugaan analog untuk dimensi setidaknya 5 dan memenangkan Fields Medal pada tahun 1966. Michael Freedman membuktikan kasus 4-dimensi dan memenangkan medali Fields pada tahun 1986.

si dimensi tinggi dari Poincaré Conjecture, dengan lebih banyak ruang untuk melakukan konstruksi geometris, lebih mudah. Stephen Smale membuktikan dugaan analog untuk dimensi setidaknya 5 dan memenangkan Fields Medal pada tahun 1966. Michael Freedman membuktikan kasus 4-dimensi dan memenangkan medali Fields pada tahun 1986.

Gagasan dasar dari bukti Perelman, menurut Richard Hamilton, adalah untuk memulai dengan manifold tiga-kompak yang terhubung dan membiarkannya menyusut pada setiap titik pada setiap arah dengan kecepatan yang sebanding dengan kelengkungan Ricci -nya . Jika Anda dapat menunjukkan bahwa Anda akhirnya berakhir dengan bola bundar, dengan bola-bola lain mungkin terjepit di sepanjang jalan, Anda dapat menyimpulkan bahwa Anda harus memulai dengan bola (cacat).

Kesulitan mendasar adalah untuk mendapatkan kontrol atas pembentukan singularitas. Untuk memfokuskan perhatian tentang hal yang menjadi perhatian, Perelman [Sect.] memberikan kepadatan berlipat ganda tentang titik itu dan memungkinkan aliran metrik oleh kelengkungan Ricci umum yang terkait, Ric ψ 18,3 ( 4 ). Jika seseorang memperbaiki ukuran, maka kerapatan berkembang sebagai persamaan panas terbalik yang dimodifikasi dan mendekati fungsi delta pada hal . Monotonitas energinya yang umum sekarang menyediakan informasi lokal yang diperlukan alih-alih informasi global yang biasa. (Sebenarnya, dalam buktinya, untuk memfasilitasi operasi, Perelman [Bagian] pindah ke versi lokal kepadatan yang disebut fungsi panjang.)

Hebatnya, modulo difeomorfisme , aliran Ricci yang digeneralisasi ini setara dengan aliran Ricci standar. Seperti yang dikatakan Perelman, “Fakta yang luar biasa di sini adalah bahwa pilihan [kepadatan] yang berbeda mengarah ke aliran yang sama, hingga difeomorfisme; yaitu, pilihan [kepadatan] analog dengan pilihan pengukur. ” Ini berarti bahwa selama pembuktian, seseorang dapat memilih kepadatan apa pun untuk kenyamanan. Singkatnya, manifold dengan kepadatan menyediakan konteks teknis yang nyaman untuk menerapkan difeomorfisme untuk memusatkan perhatian pada wilayah yang menjadi perhatian.

Selain manifold umum dengan kepadatan, contoh utama ruang Gauss membuat penampilan penting dalam bukti Perelman. Secara khusus, ketimpangan isoperimetri pada ruang Gauss dalam bentuk fungsional, yang dikenal sebagai ketimpangan Sobolev logaritmik Gaussian, merupakan unsur teknis yang penting.

Manifol umum dengan kepadatan belum muncul di sebagian besar paparan karya Perelman. Ini sebagian karena mereka muncul hanya di bagian pengantar dan digantikan oleh fungsi panjangnya di bukti yang sebenarnya. Ini juga sebagian karena manifold dengan kepadatan tidak begitu akrab dengan komunitas matematika sebagaimana mestinya. Mereka muncul dalam kalimat pertama dari tubuh kertas Perelman, di mana ia mulai dengan mempertimbangkan bermacam-macam dengan kepadatan e - f dan kelengkungan skalar R :

Pertimbangkan fungsional F = ∫ M ( R + | ∇ f | 2 ) e - f dV untuk metrik Riemannian g ij dan fungsi f pada manifold tertutup M .

Anderson, dalam survei Pemberitahuannya , membuat komentar berikut tentang diskusi Perelman tentang aliran Ricci dalam manifold dengan kepadatan:

Ternyata, mengingat setiap metrik awal g (0) dan t > 0, fungsi [kerapatan] f ... dapat ditentukan secara bebas di g ( t )…. Perelman kemudian menggunakan kebebasan ini untuk menyelidiki geometri g ( t ) dengan pilihan f . Sebagai contoh, ia menunjukkan dengan studi yang sangat sederhana tentang bentuk [energi] F bahwa keruntuhan atau noncollapse dari metrik g ( t ) di dekat titik x 0 dapat dideteksi dari ukuran F dengan memilih f untuk menjadi perkiraan untukfungsi delta berpusat di x . Semakin runtuh g ( t ) dekat x , semakin negatif nilai F . Runtuhnya metrik g ( t ) pada skala apa pun dalam waktu yang terbatas kemudian dikesampingkan dengan menggabungkan ini dengan fakta bahwa F fungsional meningkat di sepanjang aliran Ricci. Bahkan, argumen ini dilakukan sehubungan dengan fungsional invarian skala yang agak lebih rumit daripada F ; termotivasi oleh analogi tertentu dalam fisika statistik, Perelman menyebut ini fungsional entropi .

Perelman, dalam kutipan berikut dari Pendahuluannya, merujuk pada hasil nonkolaps dari §4 ini. Dia juga menyebutkan penggunaan dalam § 3 Gaussian isoperimetric kesenjangannya untuk membuktikan bahwa Anda tidak mendapatkan periodisitas alih-alih perilaku pembatasan yang diinginkan.

Kami membuktikan bahwa aliran Ricci, yang dianggap sebagai sistem dinamis pada ruang metrik Riemannian modulo difeomorfisme dan penskalaan, tidak memiliki orbit periodik nontrivial. Kasus metrik yang mudah (dan diketahui) dengan kelengkungan skalar minimum negatif diperlakukan dalam §2; kasus lainnya dibahas dalam §3, menggunakan rumus monotonisitas utama kami (3.4) dan ketidaksetaraan Sobolev logaritmik Gaussian, karena L. Gross. Dalam §4 kami menerapkan rumus monotonisitas kami untuk membuktikan bahwa untuk solusi yang halus pada interval waktu yang terbatas , jari-jari injeksi pada setiap titik dikontrol oleh lengkungan pada titik-titik terdekat. Hasil ini menghilangkan batu sandungan utama dalam pendekatan Hamilton untuk geometriisasi.

Dalam matematika, dugaan Hodge adalah masalah besar yang belum terpecahkan dalam geometri aljabar yang menghubungkan topologi aljabar dari variasi aljabar kompleks non-singular dengan subvarietasnya.

Lebih khusus lagi, dugaan tersebut menyatakan bahwa kelas kohomologi de Rham tertentu bersifat aljabar; yaitu, mereka adalah jumlah dual Poincaré dari kelas - kelas homologi subvarieties.

• Philosophy of Geometry from Riemann to Poincaré

Sementara permukaan tertutup telah diklasifikasikan terutama oleh Bernhard Riemann, klasifikasi manifold tertutup memiliki hubungan yang dalam dengan dugaan Poincaré.

Pada tahun 1982, William Thurston, mungkin topologi terhebat abad ke-20, menduga bahwa geometri dari bermacam-macam 3-manifold dapat diklasifikasikan sebagai salah satu dari 8 kemungkinan geometri.

Bukti Perelman, bersama dengan dugaan Poincaré, menjawab dugaan Thurston secara positif.

• Hamilton circuit
• Poincaré sections of Hamiltonian

Sebuah siklus Hamiltonian (atau sirkuit Hamilton ) adalah jalur Hamiltonian yang merupakan siklus .

Menentukan apakah suatu jalur dan siklus ada dalam grafik adalah masalah jalur Hamiltonian, yang merupakan NP-complete sehingga masuk dalam salah satu kasus dari Masalah P vs NP.

• The Lambda & The Tetraktys

Bahkan sebagian orang berpendapat bahwa untuk beberapa kasus sisanya bisa jadi belum akan ada pemecahan pada abad ini karena terbentur belum ditemukannya referensi khususnya pada disiplin ilmu matematika yang dapat menunjang pemecahan.

Boleh percaya boleh tidak, saat saya juga skeptis dengan kasus milenial ini maka pada waktu yang bersamaan tau² tanpa sengaja ketemu sang mistis tetraktis yang justeru menjadi titik terangnya.

Detilnya bisa Anda ikuti mulai dari bahasan tentang penyertaan objek.

Sekarang kita masuk ke kasus, dimulai dengan repository dari angka 10 yang kita setel untuk kasus yang sudah mendapatkan solusi yaitu Poincare Conjecture dengan kasus pemetaan geometri pada bidang 3 dimensi.

Berikut intisari dari kasusnya:

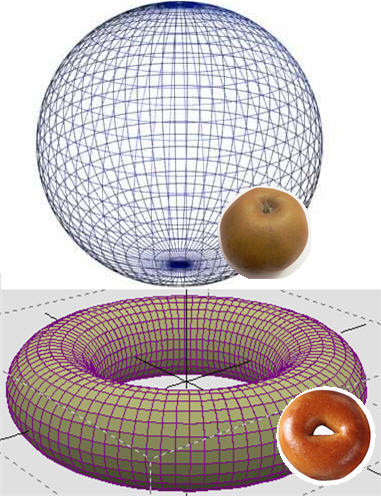
• Jika kita merentangkan karet gelang di sekitar permukaan apel, maka kita dapat mengecilkannya hingga ke suatu titik dengan menggerakkannya perlahan, tanpa merobeknya dan tanpa membiarkannya meninggalkan permukaan.
• Di sisi lain, jika kita membayangkan bahwa pita karet yang sama entah bagaimana telah direntangkan ke arah yang tepat di sekitar donat, maka tidak ada cara untuk mengecilkannya ke suatu titik tanpa memutus karet gelang atau donat.
• Kita mengatakan permukaan apel "hanya terhubung," tetapi permukaan donat tidak.
• Poincaré, hampir seratus tahun yang lalu, tahu bahwa bola dua dimensi pada dasarnya ditandai oleh sifat konektivitas sederhana ini, dan mengajukan pertanyaan yang sesuai untuk bola tiga dimensi.

Solusi yang sudah dilakukan adalah dengan menggunakan metoda Ricci Flow.

Pertama² kita tetapkan repository dengan id:10 sebagai basis. Di repository ini kita ambil kasus yang sudah menjadi solusi yaitu Poincare Conjecture.

Sekarang simak lagi skema pemetaan yang sudah saya jelaskan sebelumnya. Anda lihat bahwa objek 5x saling berhubungan dengan titik awal di id:10.

Bagaimana dengan yang 2x?

Angka sepuluh (10) ini mempunyai objek 109. Sekarang lihat objek 2x di pemetaan. Anda lihat ada dua (2) angka 109 yang berlaku sebagai vektor.

Ini artinya angka 2 akan menempel ke objek yang 109 yang berada di angka 10 sehingga kedua angka ini akan membentuk gabungan angka di 102. Nah inilah calon 102 yang akan jadi tetraktis.

Ini juga tanda bahwa objek yang 2x dan yang 5x nempelnya di angka 10 ini. Angka 109 ini adalah prime ke-29, karenanya 10 dan 2 via angka 109 ini akan meregenerasi objek turunan ke seluruh objek yang 29.

Sekarang perhatikan bagan tetraktis berikut ini:

Titik tengah nya ada pada angka 6, ini sebabnya maka hanya tetraktis yang bisa melakukan manuver di angka 6 sehingga pada gilirannya dari objek 29 tadi diteruskan sampai ujung dari 114 angka dasar semua terkoneksi dengan masing² objeknya.

114 = 6 + (6 x 6) + 6 x (6 + 6) = 6 x (6 + 6) + 6 + (6 x 6)

Saat ini terjadi maka kita lakukan pendataan koneksi² itu sehingga kita dapatkan hubungan antara angka² ini dengan objelnya masing².

Dengan demikian kita akan sampai di posisi dari setiap kasus yang kita sertakan dalam projek.

• Applying Ricci flow to high dimensional manifold learning
• Mathematics - Poincaré Conjecture Torus Mathematics Homeomorphism

Twin Primes: 
(5,7), (11,13), (17,19)

layer|  i  |   f
-----+-----+------
     |  1  | (5) -------
  1  +-----+            |
     |  2  | (7)        |
-----+-----+------      |
     |  3  | (11) ‹--3x--
  2  +-----+            |
     |  4  | (13)       |
-----+-----+------      |      
     |  5  | (17) ‹--2x--
  3  +-----+
     |  6  | (19)
-----+-----+------

Permutation:
66 = 6 & 6
6 + 6 = 12

5 + 7 = 12 = d(3)
11 + 13 = 24 = d(6)
17 + 19 = 6 x 6 = d(9)

6 + 6 » d(3,6,9) » 6 x 6

Setelah cari sana-sini ternyata itu gak jauh², dia ada di bentuk manifold torus yang sudah saya uraikan. Dan torus itu adalah.. bentuk manuver dari Sistem DNA itu sendiri.

Alasan kedua adalah..
Memang metoda Ricci Flow ini yang digunakan menggandeng bentuk torus.

Nyambung jadinya kan?

Bahkan sekarang ini dikembangkan bukan hanya bentuk² geometris melainkan sampai konversi bentuk² wajah dalam tiga (3) dimensi secara persis ke data komputer.

Jika sekarang ini Anda hanya bisa lihat persis bentuk wajah Anda di bidang datar seperti foto atau smartphone. Nah bagaimana bila dengan komputer virtual, Anda menjumpai Anda sendiri persis di depan Anda dalam tiga (3) dimensi?

Apalagi bila pake ketawa atau lari²..

Jadi dampak solusi kasus milenial ini betul² luar biasa.
Dan itu baru satu (1) kasus saja dari yang tujuh (7).

Nah sekarang kembali ke laptop. Eh maksudnya ke kasus.

Selanjutnya kita terapkan metoda ini sistem tiga (3) dimensi yang kita simulasikan.

Dengan proses yang kita lakukan sebelumnya maka pada semua repository sistem bilangan prima sudah pada posisi masing² mengikuti sifat alamiahnya pada Sistem-DNA.

Kemudian kita posisikan bidang tiga (3) dimensi ini pada Sistem DNA.

Setelah itu kita ikuti bagaimana perilaku bilangan² prima ini dalam mendapatkan solusi dengan cara membandingkannya dengan solusi yang sudah didapat.

Berikutnya kita ambil Input (I) data dari objek via Query (Q):

Suatu Query (Q) akan memunculkan Result (R) maka sistem bilangan prima akan melakukan sisanya yaitu manuver alamiahnya berupa gerakannya di Sistem DNA yaitu torus tadi:

Kita arahkan agar dapat menempelkan manuver torus ke objek.

Dan sentral dari manuver ini tak lain adalah.. angka enampuluh enam (66) itu sendiri:

6 + (6 x 6) + 6 x (6 + 6) = 6 x (6 + 6) + 6 + (6 x 6)

Ini kita lakukan sampai akhirnya muncul sang tetraktis 102. Dengan kemunculannya berarti terjadi siklus sistem maka kita sudah ada di ujung yaitu Output (O) berupa sebuah solusi.

Jadi ibaratnya seolah² dia itu bilang gini..
Dah beres kan gan, ada lagi gak?

Seperti telah dijelaskan sebelumnya metoda ini merupakan manuver angka 66 terhadap seluruh objek pemetaan.

Ini akan merupakan pemetaan dari tabulasi vektor yaitu 29 angka plus 1 repository dari hasil pemetaan sehingga jumlah totalnya nya 30 + 66 yaitu 96.

Anda bisa ikuti detilnya pada di angka sembilanpuluh enam (96) ini. Juga dengan angka² lainnya. Namun pencabangan ke banyak repository bisa menjadi bentuk pohon banyak cabang

Apalagi ada anak cucu cabangnya. Integrasi akan menjadi masalah utama iika Anda tidak menyertainya dengan mapping.

Karena itu kita perlu membuat dokumentasi dari pemetaan ini layak untuk dijadikan panduan, jika perlu kita cek akurasi dan kecepatan halaman sehingga nyaman buat yang membaca

Hal ini penting dilakukan karena jangankan orang lain, kita sendiri yang berkutat disitu bisa tersesat dan menyimpang dari target.

Apalagi dengan skema pemetaan yang gunakan banyak repository.

Maka skema pemetaaan dengan menggunakan karakter angka² dimana dia itu bisa diintegrasikan adalah merupakan kunci utamanya.

Dengan demikian seberapa besarpun skema projek yang Anda buat, baik sedikit maupun jumlah besar, tetap dia akan tetintegrasi dengan pola yang sama.

Secara keseluruhan mulai dari awal yaitu: Konsep jika kita gabungkan semuanya maka kita akan dapatkan pola dari id:10. Pola ini yang saya maksud dengan class baru dari IQRO.

id: 27

---+-----+-----
 1 | 1   | 6
---+-----+-----
 2 | 7   | 14
---+-----+-----
 3 | 15  | 44
---+-----+-----
 4 | 45  | 53
---+-----+-----
 5 | 54  | 58
---+-----+-----
 6 | 59  | 59
---+-----+-----
 7 | 60  | 69
---+-----+-----
 8 | 70  | 93
---+-----+-----

Dengan class ini kita akan gunakan untuk lanjut pada kasus² lainnya.

Proses ini dilakukan via pemrograman. Detilnya sangat panjang jika dibahas disini.

Karenanya saya tempatkan pada masing² repository terkait. Anda bisa ikuti mulai dari proses pemetaan.

Sampai disini saya cukupkan bahasan tentang topik dari subject ini.

Jika Anda ingin lanjut tuntas silahkan simak kasus pertama.

Sekian.

SALAM Sukses!
© Chetabahana Project

• Cyclic Addition Mathematics that repairs & perfects An old invention: Number
• Detecting critical node structures on graphs: A mathematical programming approach

⏫	🔼	⏪ Intro	◀️ Prev	🔁 Repo	Next ▶️	Last ⏩	🔽	⏬
	This wiki is courtesy of Chetabahana Project. Find all of them on Project Map.