05_MO_visualization - YoshioNishimoto/sandbox GitHub Wiki
分子軌道の可視化を行います。
マニュアルとしては、こちらをご参照ください。(リンクが見つからなくなりました)
一点計算のところでご紹介したとおり、分子軌道( )は基底関数(原子軌道)(
)の線形結合により表されます。
(Szabo: 式(3.133))
は分子軌道係数です。詳しくはSzabo: Sec.3.4.2や3.5.1をご参照ください。
今回可視化するのは分子軌道(
)のことです。
原子軌道と混同しないでください。
また、ここでは直交した分子軌道(canonical molecular orbitalとも呼ばれる)を可視化します。
他にも局在軌道(localized orbital)を可視化することも可能です。
後の回でやります。
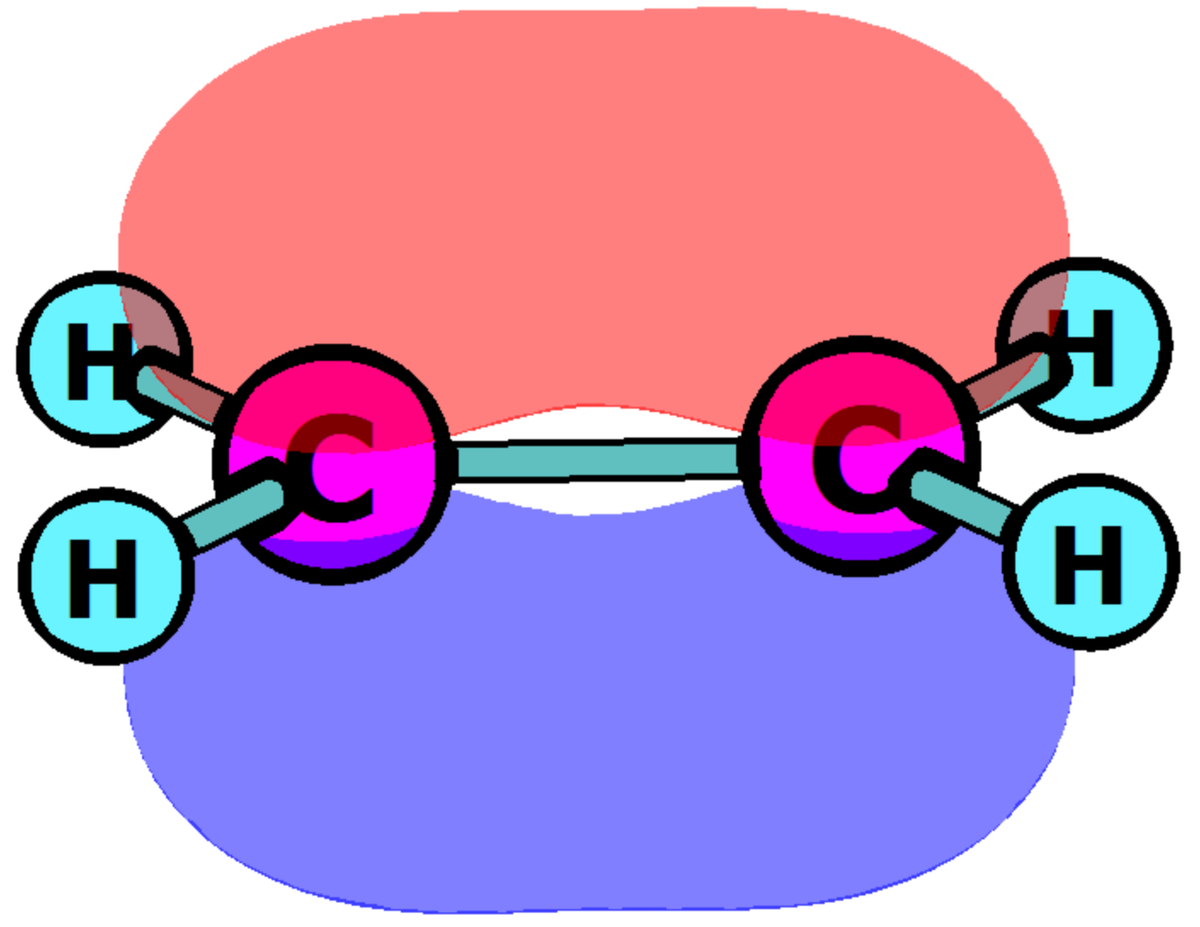
とりあえず、ここではethylene (C2H4)のπ軌道とπ*軌道、すなわち最高占有軌道(HOMO; highest occupied molecular orbital)と最低非占有軌道(LUMO; lowest unoccupied molecular orbital)の分子軌道(下図参照)を描いてみます。 なお、ここで描きたい軌道が必ずしもHOMOとLUMOに対応するかは自明ではありません。 6-31G(d)の場合は偶然にもHOMOとLUMOがそれぞれπ軌道とπ*軌道に対応します。 可視化ソフトウェア(VMDやAvogadroなど)はインストール済みとします。 私はChemcraftを用いています。
HOMO:
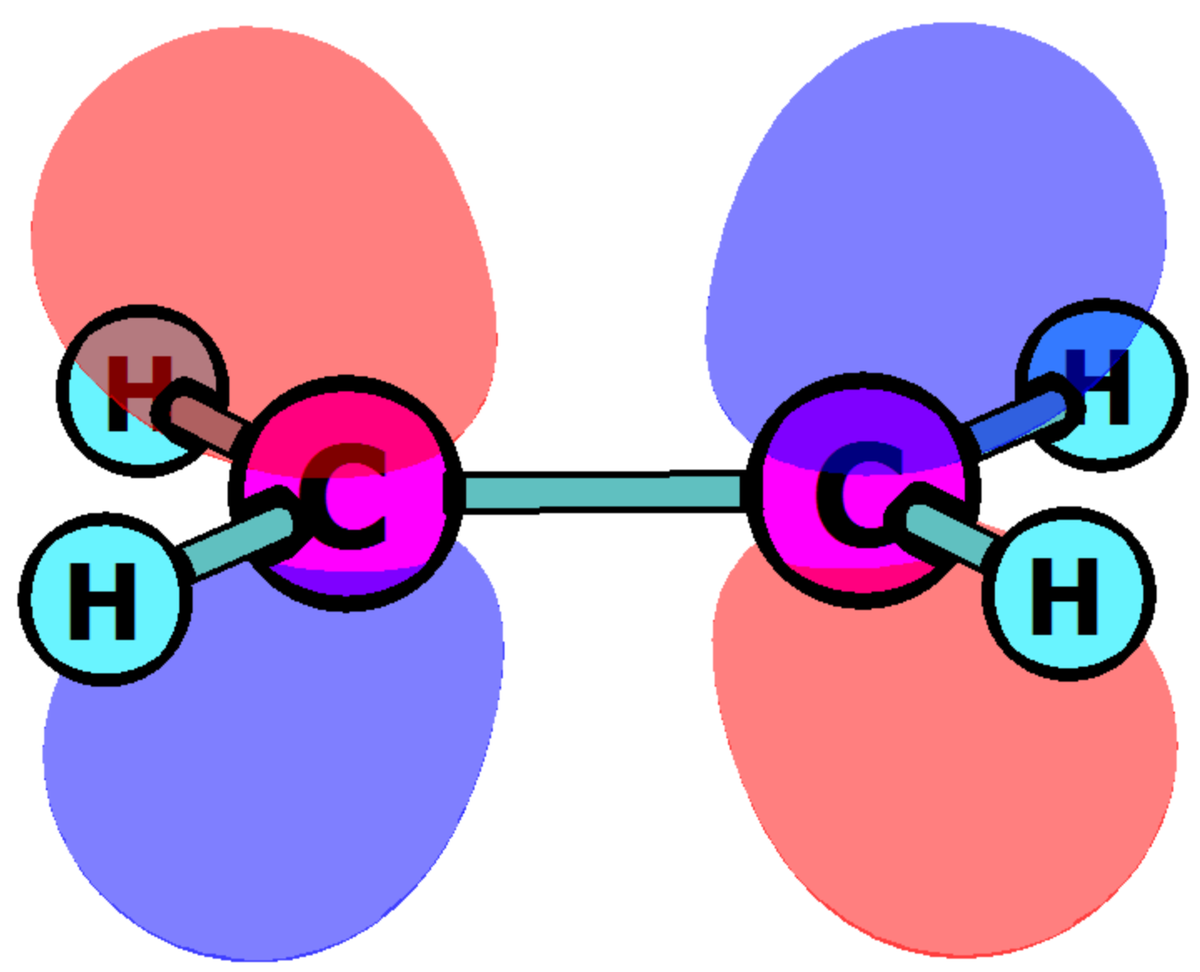
LUMO:
まずはエチレンを(R)HF/6-31G(d)レベル((R)HF/STO-3Gの方が良いかも。一般的は、小さい基底関数を用いた方が分子軌道を解釈しやすくなります)で構造最適化してみてください。 エネルギーは-78.0313607728 hartreeぐらい(数値誤差や収束判定により多少の誤差が出ます)になると思われますので、正しいか確認してください。 きちんと考えているとおりの構造になるでしょうか。 必ずしも構造最適化をしなければならないわけではありませんが、通常はするものと思います。 なお、PySCFはspherical harmonicsな(?)基底関数(d軌道に5つの軌道を用いる)を用いますが、 ソフトウェアによってはデフォルトでCartesianな基底関数(d軌道に6つの軌道を用いる)を用いる場合があります。 同じ計算をしているつもりでも、別のソフトウェアを用いると結果がわずかに変わってしまうので、注意してください。 バグっているわけではなく、ソフトウェアの性格と計算の詳細を理解して計算を行う必要があるということです。
PySCFを用いた分子軌道の可視化は二通りあります。 最初にcubeファイルを直接生成するという方法をご紹介しますが、 おそらく二つ目のMOLDENファイルを生成するという方法の方が楽です。
分子軌道を可視化するには、まず描きたい分子軌道の番号を知る必要があります。
今回の場合、ethyleneの電子数は16とわかるので、HOMOは8番目の分子軌道、LUMOは9番目の分子軌道となります。
場合によっては、分子軌道係数mo_coeffを出力して「数値から分子軌道を推測する」ということが必要かもしれません(が、現実的にはcubeファイルを出力して、目で見て判断する方が楽です)。
分子軌道の番号が分かったら、次は「cubeファイル」を出力します。 入力ファイルは以下のような感じになります。
1 from pyscf import gto, scf
2 from pyscf.tools import cubegen
3
4 mol = gto.M(verbose=4,
5 atom= [["C",( 6.00888796e-13,-5.21236125e-14,-1.27727822e+00)],
6 ["C",(-5.73985844e-13, 1.59017062e-14, 1.21246132e+00)],
7 ["H",(-2.61455155e-13, 1.72747100e+00,-2.34915037e+00)],
8 ["H",(-6.70150000e-14,-1.72747100e+00,-2.34915037e+00)],
9 ["H",( 2.48003679e-13, 1.72747100e+00, 2.28433346e+00)],
10 ["H",( 5.35635242e-14,-1.72747100e+00, 2.28433346e+00)]],
11 basis="6-31G(d)",unit="Bohr")
12 mf = scf.RHF(mol)
13 mf.kernel()
14
15 # print(mf.mo_coeff)
16
17 cubegen.orbital(mol, 'ethylene_HOMO.cube', mf.mo_coeff[:,7]) # 8th orbital
18 cubegen.orbital(mol, 'ethylene_LUMO.cube', mf.mo_coeff[:,8]) # 9th orbital2行目は「cubegen」というツールを使うために必要で、
17・18行目が実際にcubeファイルを出力する行となります。
unit="Bohr"を付けている(構造最適化の結果がBohr単位で出力されるため)ことと、
12行目で一度エネルギーを計算(すなわち分子軌道係数を得る)していることに注意してください。
17行目のcubegen.orbital(mol, 'ethylene_HOMO.cube', mf.mo_coeff[:,7])で、8番目の分子軌道をethylene_HOMO.cubeとして出力しています。
Pythonの配列はゼロから始まることに注意してください。
上記の入力ファイルでPySCFの計算を行うと、そのディレクトリ(フォルダ)にethylene_HOMO.cubeとethylene_LUMO.cubeというファイルが生成されるはずです。
[nisimoto@yn1 aaa]$ cat MO.py
from pyscf import gto, scf
...(上のファイルと同じなので省略)
[nisimoto@yn1 aaa]$ python3 MO.py > MO.out
[nisimoto@yn1 aaa]$ ls
ethylene_HOMO.cube ethylene_LUMO.cube MO.out MO.py
この新しく作成されたcubeファイルを可視化ソフトウェアに読み込ませることにより、分子軌道を見ることができます。 実際の可視化の方法は・・・ソフトウェアにより違います。 大抵はマニュアルやQ&Aに書いてあると思うので調べて実践してみてください。
ここではcubegen.orbitalを用いて分子軌道のcubeファイルを出力しました。
他にも例えばcubegen.density(mol, 'ethylene.cube', mf.make_rdm1())を用いると電子密度を出力することができます。
densityの部分をmepに変更すると、分子の静電ポテンシャルを出力できるとのことです。
他にも、スピン密度を出力してみたいところですが・・・おそらくα軌道とβ軌道それぞれの電子密度を計算して、その差を計算するスクリプトを書く必要があると思われます。
時間があれば、そのあたりも試してみてください。
ここではπ軌道とπ*軌道を見つける作業を行いました。 いつになるかは分かりませんが、今後multiconfiguration SCF(あるいはcomplete active space SCF)といった計算を行う際に、これらの軌道を見つけて(軌道の順番を変えて)から計算を行うという作業が必要になります。 今回はその準備を兼ねています。
量子化学計算ソフトウェアと可視化ソフトウェアの組み合わせによっては、
わざわざcubeファイルを作成することなく、出力ファイルを可視化ソフトウェアに読み込ませるだけで軌道を可視化させられます。
PySCFでも、マニュアルに書いてあるとおりMOLDEN用のファイルを作成するとできます。
1 from pyscf import gto, scf
2 from pyscf.tools import molden
3
4 mol = gto.M(verbose=4,
5 atom= [["C",( 6.00888796e-13,-5.21236125e-14,-1.27727822e+00)],
6 ["C",(-5.73985844e-13, 1.59017062e-14, 1.21246132e+00)],
7 ["H",(-2.61455155e-13, 1.72747100e+00,-2.34915037e+00)],
8 ["H",(-6.70150000e-14,-1.72747100e+00,-2.34915037e+00)],
9 ["H",( 2.48003679e-13, 1.72747100e+00, 2.28433346e+00)],
10 ["H",( 5.35635242e-14,-1.72747100e+00, 2.28433346e+00)]],
11 basis="6-31G(d)",unit="Bohr")
12 mf = scf.RHF(mol)
13 mf.kernel()
14
15 with open('C2H4mo.molden', 'w') as f1:
16 molden.header(mol, f1)
17 molden.orbital_coeff(mol, f1, mf.mo_coeff, ene=mf.mo_energy, occ=mf.mo_occ)
2行目でmoldenを出力する関数を読み込んでいます。
15から17行目で「C2H4mo.molden」というものを出力してくれます。
17行目のene=mf.mo_energyは分子軌道の軌道エネルギー、occ=mf.mo_occは軌道の電子占有数(占有軌道が2.0で非占有軌道が0.0)を意味しています。
こうして出力した「C2H4mo.molden」というファイルをMOLDENやAvogadroなどの可視化ソフトウェアで読み込むと、可視化することができます。
こちらの方法では、可視化ソフトウェアを操作するだけで別の分子軌道を見ることができます。 一方最初にご紹介した方法では、PySCFでcubeファイルを生成してから可視化ソフトウェアに読み込ませて可視化します。 どちらが使いやすいかは人によりますし、いろいろ考え方があるので何とも言えませんが、 見つけたい軌道がどのエネルギー準位にあるか分からない場合は、こちらのMOLDENファイルを経由した方が便利と思います。
- 同じく、cc-pVDZとaug-cc-pVDZという基底関数を用いて、それぞれethyleneのπ軌道とπ*軌道をプロットしてみましょう。 cc-pVDZを用いた場合には、先ほどと同じように8番目と9番目の軌道で良いかもしれません。 一方でaug-cc-pVDZの場合は8番目と9番目に対応するかは分かりません。 どのあたりまで軌道をチェックする必要があるでしょうか。 この"aug-" (= augmentation)はdiffuse関数と呼ばれています。 ガウス関数の指数部分が小さい関数(空間的には大きな関数)のことで、 通常は電気陰性度が高い元素に対して用いる傾向が高いです。
- 同様に、HF/6-31G(d)かHF/cc-pVDZレベルで1,3-butadiene (C4H6)と1,3,5-hexatriene (C6H8)のπ軌道とπ*軌道をプロットしてみましょう。 すべてE体?(trans体?ジグザグ?)で良いです。
- Re2Cl82-のδ結合を発見できるか試してみましょう。基底関数は、とりあえずLanL2DZとかが良いと思います。