carry lookahead adder - mbits-mirafra/digitalDesignCourse GitHub Wiki

Carry lookahead adder

Carry Look Ahead Adder is an improved version of the ripple carry adder.
It generates the carry-in of each full adder simultaneously without causing any delay.
The time complexity of carry look ahead adder is constant and does not depend upon the number of bits in operand.

carry lookahead adder

Working principle:

The carry-in of any stage full adder is independent of the carry bits generated during intermediate stages.

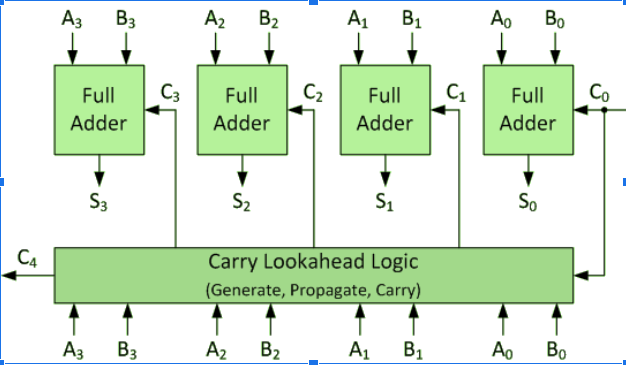
4-bit carry look ahead adder:

Consider two 4-bit binary numbers A3A2A1A0 and B3B2B1B0 are to be added.

Generally Cout in full adder is given as

              Cout = Cin(A xor B) + A.B

We have, C1 = C0 (A0 ⊕ B0) + A0B0

                 C2 = C1 (A1 ⊕ B1) + A1B1

                 C3 = C2 (A2 ⊕ B2) + A2B2

                 C4 = C3 (A3 ⊕ B3) + A3B3

Gi = AiBi where G is called carry generator

Pi = Ai ⊕ Bi where P is called carry propagator

               C1 = C0P0 + G0 ………….. (1)

               C2 = C1P1 + G1 ………….. (2)

               C3 = C2P2 + G2 ………….. (3)

               C4 = C3P3 + G3 ………….. (4)

Now,

Clearly, C1, C2 and C3 are intermediate carry bits.

So, let’s remove C1, C2 and C3 from RHS of every equation.

Substituting (1) in (2), we get C2 in terms of C0.

Then, substituting (2) in (3), we get C3 in terms of C0 and so on.

Finally, we have the following equations-

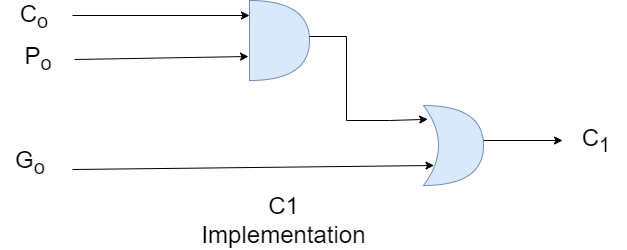
                  C1 = C0P0 + G0 

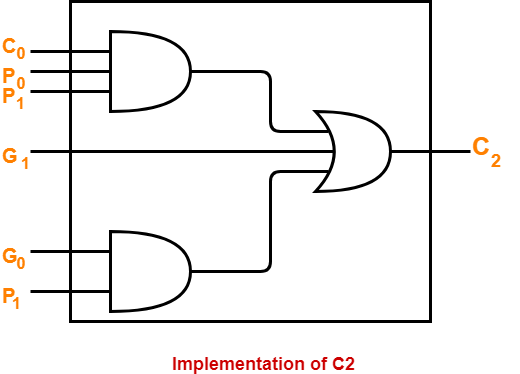
                  C2 = C0P0P1 + G0P1 + G1

                  C3 = C0P0P1P2 + G0P1P2 + G1P2 + G2

                  C4 =C0P0P1P2P3 + G0P1P2P3 + G1P2P3 + G2P3 + G3

Implementation of carry generator:

Two level combinational circuits.
Using AND and OR gates where gates are assumed to have any number of inputs.

Implementation of C1:

Implementation of C2:

Implementation of C3 and C4:

Similarly, we implement C3 and C4.

Implementation of C3 uses 3 AND gates and 1 OR gate.
Implementation of C4 uses 4 AND gates and 1 OR gate.