To Do Non Deterministic Finite State Machines - mbits-mirafra/digitalDesignCourse GitHub Wiki

A Non-Deterministic Finite State Machine (NDFSM) is a 5-tuple (Q, Σ, δ, q0, F), where:

Q is a finite set of states.
Σ is a finite alphabet of input symbols.
δ: Q × (Σ ∪ {ε}) → P(Q) is a transition function that maps a state and an input symbol (or ε) to a set of possible next states.
q0 ∈ Q is the initial state.
F ⊆ Q is a set of accepting/final states.

In an NDFSM, for each input symbol (or ε), there can be more than one possible transition from a given state. This means that the machine may have multiple next states for a given input symbol (or ε) in a given state. Epsilon (ε) is a special symbol used to denote an empty transition or a transition that occurs without any input.

Consider an example,

Take the case of an elevator. If one were to enter an elevator at the ground floor and wished to go to the 5th floor, the elevator will go directly to the 5th floor. But if someone on floor 1-4 also wished to go to floor 5, the elevator would stop at that floor and then proceed to the 5th floor. The final state, i.e., 5th floor stays the same, but the path will change accordingly.

Consider another example given below to be the flow of a transcription tool like Google Voice Search. The sentence in phonetic is

ˈflaɪɪŋ pleɪnz meɪks miː ˈhæpi.

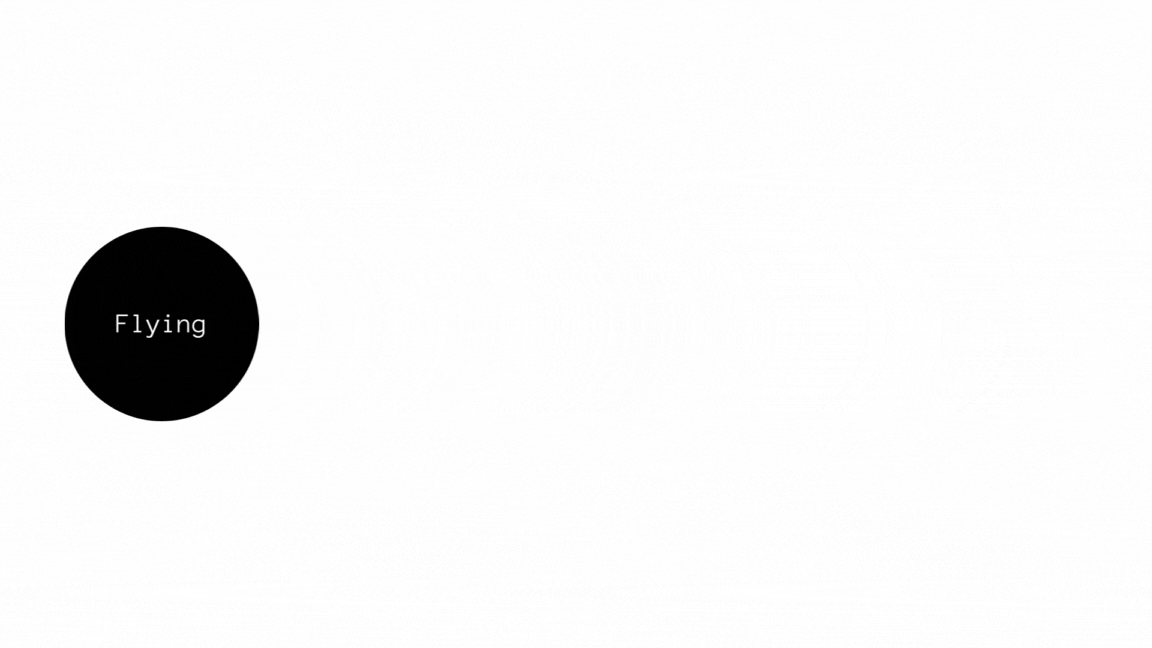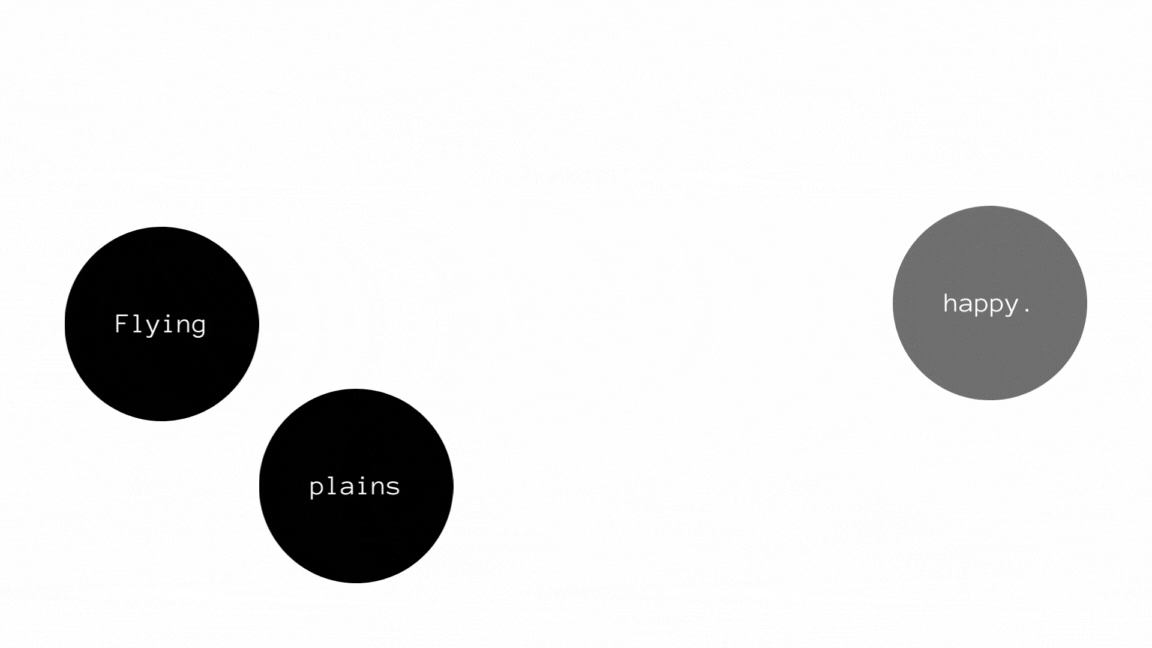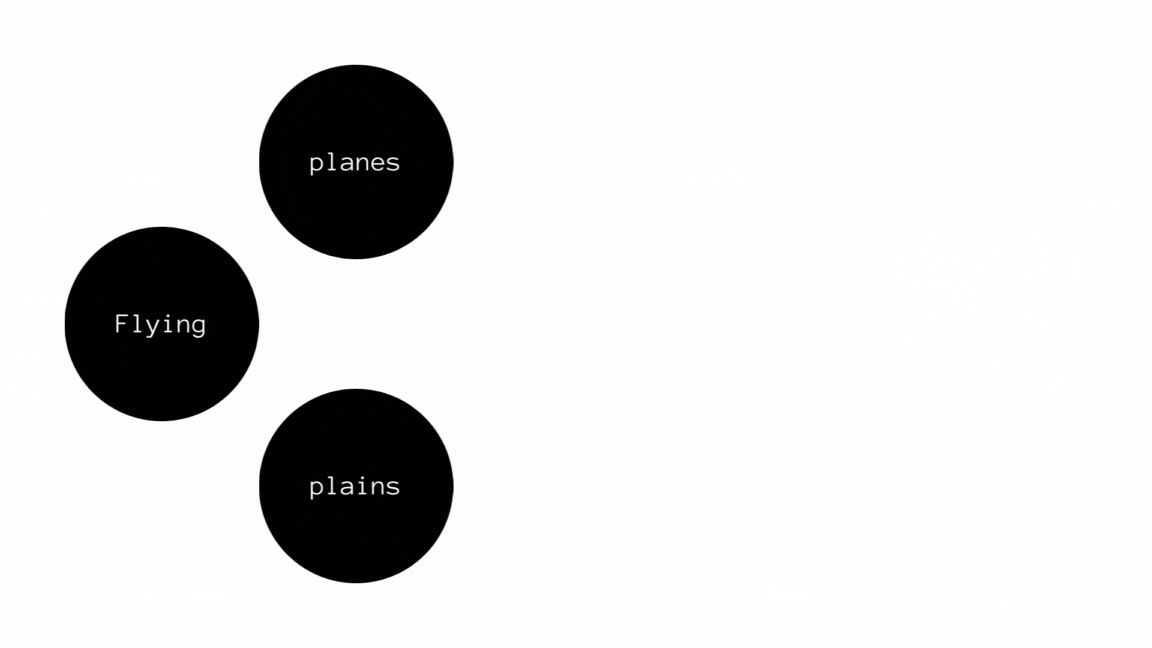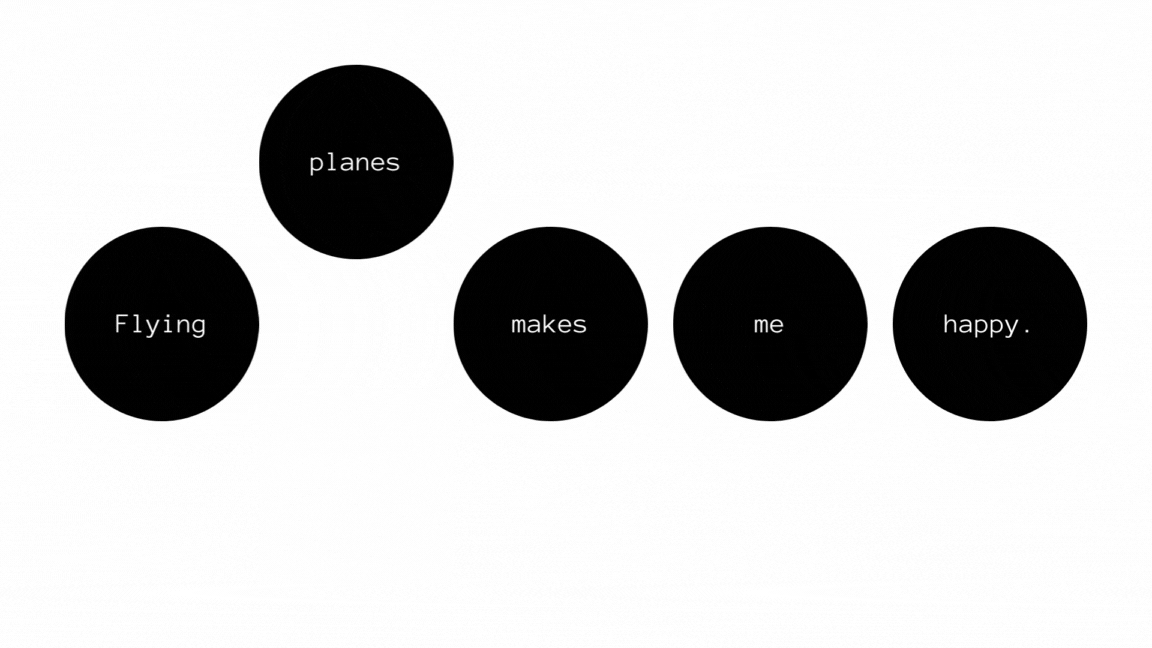
The sentence can either be "flying plains makes me happy" or "flying planes makes me happy". Given the full context, "flying planes" makes more sense compared to "flying plains". This shows that NDFSMs are used where self-correction can be made with the help of constraints and that most importantly, they can have multiple paths to a final output.

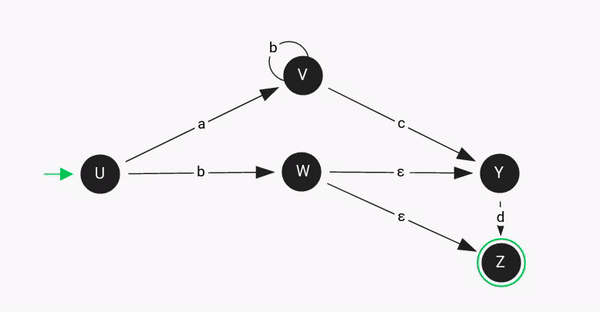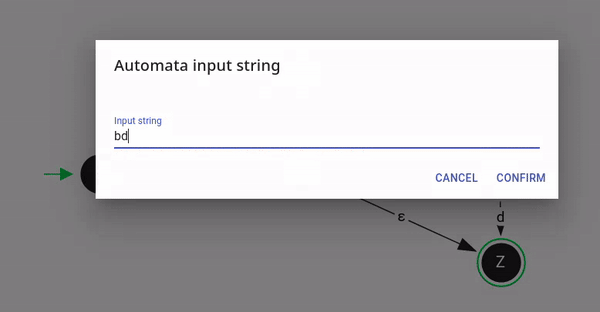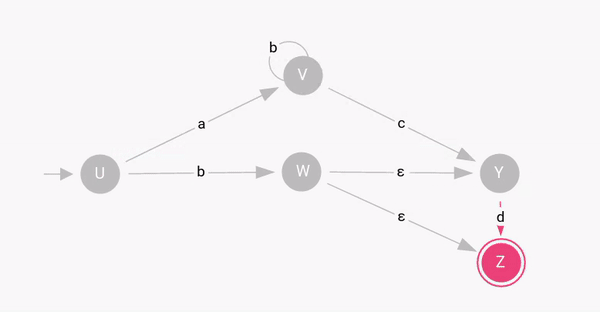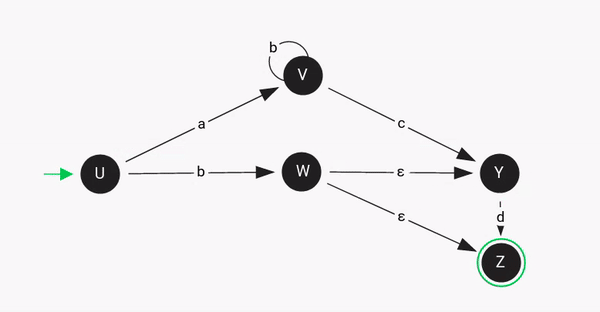
In the given example, the input string "bd" leads to 2 different paths, i.e, "bƐd" and "bƐ".

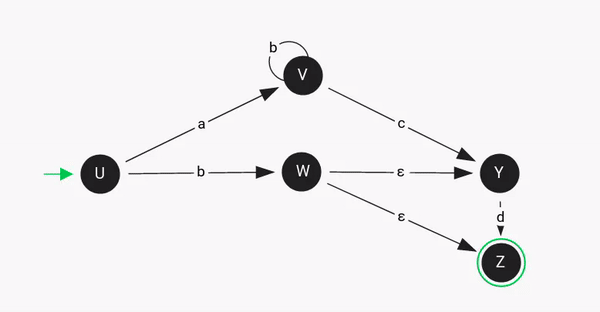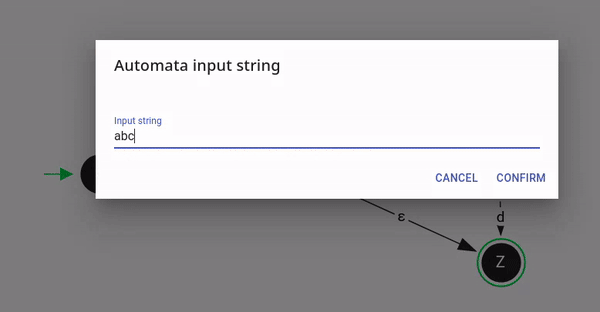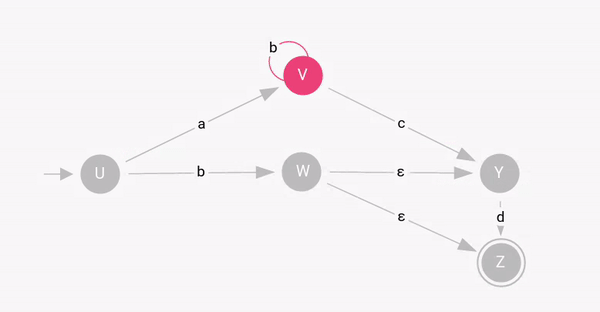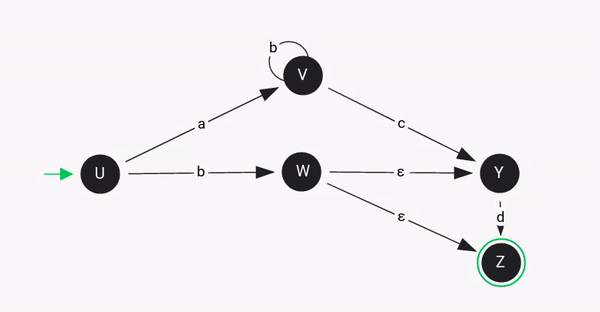
An NDFSM can also act like an DFSM like in the above example when the given input string "abcd" provides a defined path.