Quine McCluskey Method

What is Quine McCluskey minimization technique ?

The Quine-McCluskey method is a Boolean algebra-based technique used for simplifying Boolean expressions.

Why to use Quine McCluskey Method ?

By simplifying Boolean expressions using the Quine-McCluskey method, it becomes easier to analyze and optimize digital circuits. A simpler expression can result in a circuit with fewer logic gates, which can lead to lower power consumption, faster operation, and reduced cost.

When to use Quine McCluskey method ?

The Quine-McCluskey method can be used to simplify any Boolean expression, but it is particularly useful when dealing with complex expressions that have a large number of variables and minterms. It is also useful when it is necessary to optimize a digital circuit by reducing the number of logic gates required to implement it. Quine McCluskey method is used when the variables are more than 5 otherwise K-Maps are used.

Procedure for Quine McCluskey method

• Arrange all the minterms, in a list of increasing order, make groups such that it contains same number of 1's.
• Create a new table showing the minterms in group n that matched with those from group n + 1 such that they differ in only one position. This process is repeated until all of the minterms in each group have been compared to those in the next higher group. When a minterm in a group is combined with a minterm in an adjacent group, a dash (-) is used to indicate an eliminated variable. As each minterm from a group combines with it is now part of a larger group. If a minterm did not combine with another, then no check would be made. If a term doesn’t simplify it is a prime implicant.
• All of the adjacent minterm groups, are compared to see if groups of four can be made.
• Repeat the process until step 3. In this case both dashes must be in the same bit position with only one other variable allowed to change. The creation of a new table further groups the sets of minterms. This same process is repeated until no further combination of minterm group is possible.
• All non checked minterm groups are now considered to be prime impliants.
• All of the prime implicants are formed into a prime implicant table.
• Evaluate the prime implicants by circling those minterms that are contained in only one prime implicant. Circled minterms represent essential prime implicants.

Example

Simplify the following Boolean function by using a Quine McCluskey minimization technique

ABCD	Y
0.	1
1.	1
2.	1
3.	1
4.	0
5.	0
6.	1
7.	1
8.	1
9.	1
10.	0
11.	0
12.	0
13.	0
14.	1
15.	1
Y = f(A, B, C, D) = ∑m (0, 1, 2, 3, 6, 7, 8, 9, 14, 15)

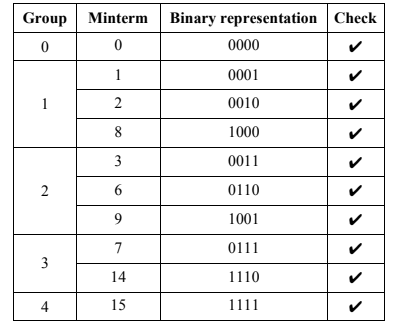
• Arrange all the minterms in increasing order and make a group such that each minterm in the group contain same number of 1s as shown in table 1.2. Group 0 contains only those minterms with no 1s, Group 1 contains only those minterms with single 1s, Group 2 contains only those minterms with two 1s, Group 3 contains only those minterms with three 1's, Group 4 contains only those minterms with four 1's as shown in table below.
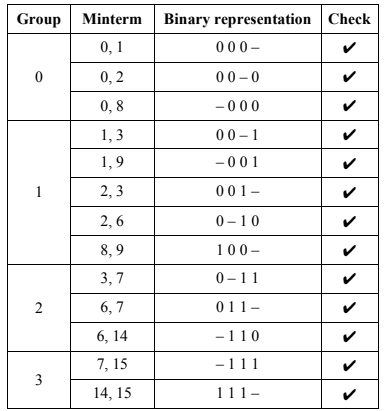
• Create a new table showing the minterms in group n that matched with those from group n + 1 such that they differ in only one position. This process is repeated until all of the minterms in each group have been compared to those in the next higher group. When a minterm in a group is combined with a minterm in an adjacent group, a dash (-) is used to indicate an eliminated variable.
• When all of the minterm in group 0 is compared with those in group 1 then compare the minterms in group1 with those in group 2.
• This process is repeated until all the minterm in each group is compared with those in the next higher group. *When a minterm from a group combines with a minterm in the next higher group then it is checked (✔). If a minterm does not combine with another then no check would be made. If a term does not simplify then it is a prime implicant.

• All of the adjacent minterm groups in table 1.4 is compared with the next higher group to see if groups of four can be made. When group of four is made the dashes (–) in the groups of two must be in the same bit position and only one variable change (0 in one group and 1 in another group) is allowed
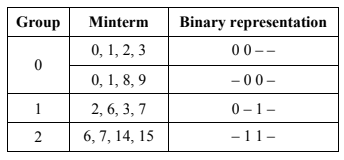
• Repeat the previous steps until no further combination of minterms groups is possible. When further grouping is made the dashes must be in the same bit position with only one other variable is allowed to change. The creation of a new table further groups the sets of minterms.
• All the non checked minterm groups are prime implicants.
• Prime implicant table is prepared using all the non checked minterm groups as shown in table 1.5.
• Each prime implicant is listed vertically in two forms: PI terms and the decimal notation of minterms.
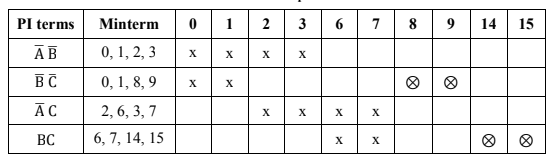
• Evaluate the prime implicants by circling those minterms that are present in only one prime implicant i.e. only one x in a column. Circled minterm represent essential prime implicant (EPI).
• To represent the simplified boolean expression select all the essential prime implicants are considered along with the other prime implicants such that all the minterms should be covered. Minterm (2, 3) are present in both the prime implicants so select any one of these prime implicant to cover all the minterms in the equation but not both.
• Therefore the simplified boolean expression is Y = B' C' + BC + A'B' or Y = B'C' + BC + A'C

Example for 5 Variables

Simplify the following Boolean function by using a Quine McCluskey minimization technique Y = f(A, B, C, D, E) = ∑m (0,1,9,15,24,29,30)

This can be also written in the form of SOP as A'B'C'D'E'+A'B'C'D'E+A'BC'D'E+A'BCDE+ABC'D'E+ABCD'E+ABCDE'

• Arrange all the minterms in the ascending order in their binary representation.

Decimal Number	Binary Representation
0	00000
1	00001
9	01001
15	01111
24	11000
29	11101
30	11110

• The next step is Grouping. Here we will group the minterms based on the number of 1's they have in them. There are 5 variable so there will be 5+1= 6 groups.

Group	Minterm	Binary Representation	Check
Group 0	0	00000	✓
Group 1	1	00001	✓
Group 2	9	01001	✓
	24	11000
Group 3	-	-
Group 4	15	01111
	29	11101
	30	11110
Group 5	-	-

The next step is to reduce the equations. We go for the 1st Reduction. Here we club the elements in the nth group with (n+1)th group if they have a difference of 1 bit. 1st Reduction

Group	Minterms	Binary Representation
Group 0	(0,1)	0000-
Group 1	(1,9)	0-001
Group 2	-	-
Group 3	-	-
Group 4	-	-

A check mark is applied for all the minterms that can be grouped in the 1st table.

The grouped minterms can be reduced to the following equation A'B'C'D' + A'C'D'E

The minterms that are not grouped can be written as A'BCDE + ABC'D'E' + ABCD'E + ABCDE'

The Final Expression is given by A'B'C'D' + A'C'D'E + A'BCDE + ABC'D'E' + ABCD'E + ABCDE'

The initial equation A'B'C'D'E' + A'B'C'D'E + A'BC'D'E + A'BCDE + ABC'D'E + ABCD'E + ABCDE' has been reduced to A'B'C'D' + A'C'D'E + A'BCDE + ABC'D'E' + ABCD'E + ABCDE'