K Map - mbits-mirafra/digitalDesignCourse GitHub Wiki
What is a K-map or Karnaugh Map?
Karnaugh Maps, or K-maps for short, are a graphical method used to simplify Boolean algebra expressions. They provide a way to visualize the logical relationships between variables in a Boolean expression and make it easier to identify groups of terms that can be combined to create a simplified expression. K-maps are commonly used in digital circuit design to optimize logic circuits and reduce the number of gates needed to implement a given function. Overall, K-maps are a powerful tool for simplifying Boolean expressions and optimizing digital circuits.
Alternatives for K-Maps
- Quine-McCluskey
- Algebraic Simplification
Advantage of K-Maps over its alternatives
- K-Maps are graphical representation of Boolean expressions, which is easier to analyze than other methods.
- K-Maps are easier to use for Boolean expressions with fewer variables.
- With K-Maps it is easy to visually confirm that the simplified expression is right.
Types of K-Maps
1 Variable K-Map
For 1-variable K-Map there will be 2^1 = 2 cells in the K-Map

The value of the minterms are written inside the K-Map
2 Variable K-maps
For 2 variable K-Map there will be 2^2 = 4 cells in the K-Maps

3 Variable K-maps
For 3 Variable K-Map there will be 2^3 = 8 cells in the K-Map

4 Variable K-maps
for 4 Variable K-Map there will be 2^4 = 16 cells in the K-Map

5 Variable K-Maps
For 5 Variable K-Map there will be 2^5 = 32 cells in the K-Map

Simplifying Minterm Equation (SOP expressions) using K-Maps
- Plot the K-map and place 1's in those cells corresponding to the 1's in the truth table or SOP expression. Place 0's in other cells.
- Check the K-map for all possible valid adjacent 1's and form a group of 2n-1's and encircle those 1's which are not adjacent to any other 1's. They are called isolated 1's.
- While grouping make sure that there is minimum no. of groups.
- Then form the simplified expression by summing product terms of all the groups.
Example
Simplify the following expression using K-map
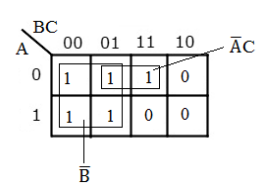
Y = AB'C + A'B'C + A'BC + AB'C' + A'B'C'
- Plot 3-variable K-map for given expression.
- Place 1's in the cell 0, 1, 3, 4, 5 and 0's in the remaining cells.
- 1's in cell 3 and cell 1 are adjacent which can be grouped (group 1)
- 1's in cells 0, 1, 4 and 5 are adjacent which can be grouped (group 2)
- When all the 1's are grouped, the minimized expression can be generated. In group-1 B is eliminated and in group-2 variable A and C are eliminated.
- Therefore the minimized expression is Y = A'C + B'
Simplifying Maxterm Equation (POS expressions) using K-Maps
- Plot the K-map and place 0's in those cells corresponding to the 0's in the truth table or POS expression. Place 1's in other cells.
- Check the K-map for all possible valid adjacent 0's and form a group of 2n-0's and encircle those 0's which are not adjacent to any other 0. They are called isolated 0's.
- While grouping make sure that there are minimum no. of groups.
- Then form the simplified expression by taking product of sum terms of all the groups.
Example
Simplify the following expression using K-map
Y = (A + B + C') (A + B' + C') (A' + B' + C') (A' + B + C) (A + B + C)
- Plot 3-variable K-map for given expression.
- Place 0's in the cell 0, 1, 3, 4, 7 and 1's in the remaining cells.
- 0's in cells 0, and 4 are adjacent which can be grouped (group 1)
- 0's in cells 1, and 3 are adjacent which can be grouped (group 2)
- 0's in cells 3 and 7 are adjacent which can be grouped (group 3)
- When all the 0's are grouped, the minimized expression can be generated. In group-1 variable A can be eliminated, in group=2 variable B is eliminated and in group-3 variable A is eliminated.
- Therefore the minimized expression is Y = (B + C)(A + C') (B')

Incompletely specified functions(Don't care terms)
- When an output value is known for every possible combination of input variables, the function said to be completely specified.
- When an output value is not known for every possible combination of input variables, the function said to be incompletely specified i.e. the truth table does not generate an output value for every possible combination of input variables.
- The minterms or maxterms that are not used as a part of the output functions are called don’t care terms denoted by 'x' or 'd' or '–' in the k-map.
- If a don’t care term can be used to create a larger group of minterms then it is assigned 1 otherwise it is assigned 0.
- For example consider the three variable truth table the output Y is incompletely specified for input conditions 110 and 111.

- From the truth table the expression is written as Y = f(A, B, C) = ∑m(1, 3, 5) + ∑d(6, 7)

- Don’t care term in cell 7 is considered as 1 and group of four (cell 1, 3, 5, 7) is done to get expression Y = C.