Curve Surfing - mammenx/synesthesia_zen GitHub Wiki

HOME > TECHNICAL DOCUMENTATION > CURVE SURFING

My life is one long curve, full of turning points. - Pierre Trudeau

When compiling the feature list for what exactly Grapheme should do, it became clear that having dedicated HW logic for drawing straight lines alone would only take it so far. Some form for HW offloading should be there for rendering circles, parabolas, ellipses etc.

Imagine Fido without curves?

But having dedicated logic for each type of curve would consume large amounts of logic elements. How about having a generic parameterized curve rendering engine capable of drawing any quadratic curve. First thoughts were on extending the Bressenham's Midpoint method to the generic quadratic equation:

Many differentials later, the logic was just too complex and was not going anywhere.

To quote from wikipedia,

The mathematical basis for Bézier curves — the Bernstein polynomial — has been known since 1912, but its applicability to graphics was understood half a century later. Bézier curves were widely publicized in 1962 by the French engineer Pierre Bézier, who used them to design automobile bodies at Renault. The study of these curves was however first developed in 1959 by mathematician Paul de Casteljau using de Casteljau's algorithm, a numerically stable method to evaluate Bézier curves, at Citroën, another French automaker.

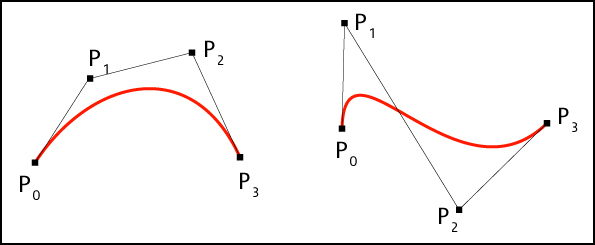
One of the cool things about Bezier curves is that a complete curve can be defined using just N+1 parameters, N being the order of the curve. Consider the below cubic Bezier curves below:

The other great feature of Bezier curves is that the algorithm for generation them is very simple and can be readily implemented in hardware.

How exactly does the algorithm work? This video explains the concept very concisely.

As the number of control points increases, the order of the curve increases i.e. more number of "curves" or turning points can be controlled in the same line.

Obviously, higher order Bezier curves will be more complex and consume more logic. It is however possible to create complex high order Bezier curves by breaking it down into simpler less order ones. This is known as a Bezier Spline.

In Synesthesia, there is support for only cubic Bezier rendering in Hardware; SW will need to patch together multiple curves to create complex paths. The Euclid sub-module in Grapheme has the logic for generating quadratic Bezier curves.

Rather then using a general parameter t, a recursive midpoint version of De Casteljau's algorithm is used.

Start with the 3 control points {P0,P1,P2}. Find the midpoints M0,M1,M2 of the line segments {P0,P1} {P1,P2} and {M0,M1} respectively. Now repeat with new control points {P0,M0,M2} and {M2,M1,P2} until the required depth is reached. Then instruct the Bressenham Line logic to plot straight lines between the control points at this depth.

draw_bezier (P0,P1,P2,depth):
  M0 = midpoint of {P0,P1}
  M1 = midpoint of {P1,P2}
  M2 = midpoint of {M0,M1}

  if(depth == 0):
    draw_line(P0,P1)
    draw_line(P1,P2)
  else:
    draw_bezier(P0,M0,M2, depth - 1)
    draw_bezier(M2,M1,P2, depth - 1)
  endif

  return