Creating a new tree - arklumpus/TreeViewer GitHub Wiki

In addition to visualising exsting trees, TreeViewer can also be used to create trees using some simple algorithms. These include the Neighbour-Joining and UPGMA methods to create trees from biological data (such as sequence alignments or distance matrices), and various models for sampling random trees (PDA, YHK, coalescence, birth-death process).

No data is required to sample a random tree using TreeViewer. Using a random tree can be useful e.g. if you want to try some new plot settings without having to find an actual tree file, or to create and inspec prior tree distributions. All methods to build trees in TreeViewer can use a constraint tree, therefore they can be used to generate trees with fixed relationships between certain taxa, while allowing other taxa to appear in unrestricted positions in the tree.

The following random tree models are currently implemented in TreeViewer (all producing bifurcating trees):

• Models generating a topology: these models generate a topology without associated branch lengths. Branch lengths can be assigned a posteriori to the branches of the tree by drawing them from a random probability distribution, but they do not form part of the model.

  • PDA model: all labelled tree topologies have the same probability.

  • YHK model: pure-birth process.

• Models generating a clock-like tree: these models simulate a tree using a unit of time, and produce trees with branch lengths, which are generally clock-like trees.

  • Coalescent model: this model produces trees that are top-heavy, by sampling the waiting time until two tips of the tree are joined.
  • Birth-death process model: This model produces trees using a birth-death process, in which each taxa has a certain probability to undergo a diversification (birth) or extinction (death).

The PDA (Proportional to Distinguished Arrangements) model, also known as the uniform model, is conceptually the easiest model implemented in TreeViewer. To "grow" a tree with a certain number of tips, the model starts with an unrooted tree with three tips. At every step, a new tip is "grafted" onto any of the existing branches in the tree. The process goes on until the required number of tips is reached:

As a result, all labelled topologies have the same probability. For example, when considering the 105 possible unrooted labelled topologies with 6 tips, each has probability $\frac{1}{105}$. However, when considering the 2 unrooted unlabelled topologies that are possible with 6 tips, they have different probabilities ($\frac{1}{7}$ and $\frac{6}{7}$):

To create a random tree under the PDA model, click on the New item in the File menu, then select Random tree and make sure that the PDA model is selected. You now need to enter:

• The number of random trees to create: this can be set to 1 to create a single tree, or to a higher number to sample an ensemble of random trees that can be used for further analyses.

• The number of tips in the tree.

• Whether the tree is labelled or not. If the tree is labelled, the labels can be specified:

  • Automatically (every time you change the value of the number of tips, the tip labels are regenerated, with values such as t1, t2 ... tN, where N is the number of tips).
  • Manually, by clicking the View/edit button and entering one tip label per line. The number of tips will automatically be set to the number of lines that are entered.
  • From the current tree (which will also adjust the number of tips correspondingly).
  • By loading a text file containing one tip label per line (again, the number of tips will be adjusted accordingly).

• Whether the random tree should be constrained or not. The constraint that is applied corresponds to the tree that is currently open in the window in which you created on the New menu item. To apply the constraint, click on the Load from tree button. To remove the constraint, click on the Remove button. The constraint will only be applied to those tips that are present both in the constraint tree and in the random tree. The constraint tree can be multifurcating; in this case, the multifurcations in the tree will be resolved randomly.

• Whether the tree is rooted or not.

• Whether the tree has branch lengths or not, and from which distribution the branch lengths are drawn (chosen from a Uniform distribution specified by its minimum and maximum values, a Gamma distribution specified by the $\alpha$ and $\beta$ parameters, and an Exponential distribution specified by the $\lambda$ parameter).

Once you are satisfied with the settings, click on the Create tree button to create the random tree. The tree(s) will open in TreeViewer and you can work on it as usual (including e.g. saving it as a Newick file from with the Save item from the File menu).

If you have applied a constraint while creating the tree, the backbone corresponding to the constraint will be highlighted in the new tree, e.g.:

In the YHK (Yule-Harding-Kingman) model (Harding, 1971), also known as the Yule model, instead, at each step the new tip can only be added as a sibling to an existing tip (i.e., it cannot be grafted onto an internal node):

As a result, the labelled topologies have different probabilities: for example, for a tree with 6 tips, there are two classes of labelled topologies, one containing 15 topologies that have a probability of $\frac{2}{150}$ each, and the other containing the remaining 90 topologies with probability $\frac{2}{225}$ each. These classes correspond to the two possible unlabelled topologies, one of which has probability $\frac{1}{5}$, and the other with probability $\frac{4}{5}$:

To create a random tree under the YHK model, follow the same steps as for the PDA model, but select the YHK model instead. You will have the same options between which to choose.

It is worth noting that if a constraint is used with the YHK model, the constraint will be enforced at every step of the growth of the tree. This will cause a bias in the distribution of the sampled topologies, in the sense that, if $\mathbb{P}_{YHK}\left (\tau \right)$ is the probability of a topology $\tau$ under the YHK model and $\mathbb{P}_{YHK}^C\left (\tau \right)$ is the probability of the topology under the YHK model with a constraint, then given two topologies $\tau_1$ and $\tau_2$, you can have that:

$$\frac{\mathbb{P}_{YHK}\left (\tau_1 \right)}{\mathbb{P}_{YHK}\left (\tau_2 \right)} \neq \frac{\mathbb{P}_{YHK}^C\left (\tau_1 \right)}{\mathbb{P}_{YHK}^C\left (\tau_2 \right)}$$

The coalescent model (Kingman, 1982) works backwards: starting from the specified number of lineages, after a certain amount of "time" two of the lineages that are currently "alive" coalesce, reducing the number of living lineages by one. This is repeated until there is only one lineage alive, which corresponds to the root of the tree. The amount of time that passes between two steps is drawn from an exponential distribution with parameter $\lambda=\frac{N_t\cdot\left(N_t - 1 \right)}{4}$, where $N_t$ is the number of lineages that are alive at step $t$:

As $N_t$ gets smaller after each step, the expected value of the waiting time increases (see figure on the right); as a result, trees sampled under the coalescent model tend to be "top-heavy", because most coalescence events happen near the tips of the tree (where $N_t$ is bigger).

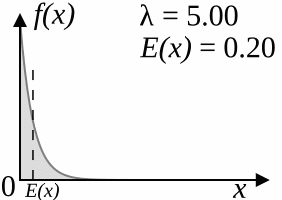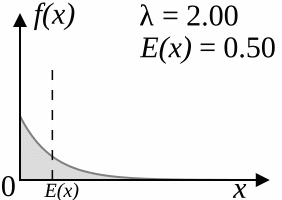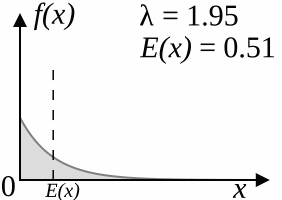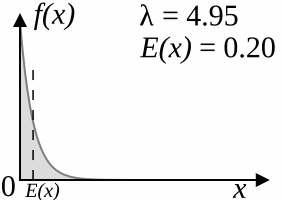
As a result of the simulation process, trees produced by the coalescent trees are clock-like; however, if you disregard the branch lengths, the topologies sampled by the coalescent model have the same distribution as the YHK model.

To simulate one or more trees under the coalescent model in TreeViewer, follow the same steps as for the PDA or YHK model, but select the coalescent model instead. Here, you can still choose how many trees to simulate, whether the tree(s) should be labelled or not, and how many tips should be included; however, the tree will always be rooted and with clock-like branch lengths.

As mentioned for the YHK model, creating a constrained coalescent tree will cause a bias in the distribution of the sampled topologies.

Under the birth-death model, the tree simulation starts from two lineages; after a certain amount of time, each lineage has the possibility of either "giving birth" to two descendant lineages, or "dying" and becoming extinct. The process then continues, with each lineage producing new descendants or becoming extinct; the simulation stops when the requested number of lineages have been generated. The waiting time between two events depends on the "birth rate" ($\lambda$) and the "death rate" ($\mu$), and it is exponentially distributed; the relative frequency of birth and death events depends on the ratio of the two rates:

As with the coalescent model, the trees produced by this process are clock-like; similarly, the tree topologies (once branch lengths are removed) are sampled with the same frequency as under the YHK model.

To simulate one or more trees under the coalescent model in TreeViewer, follow the same steps as for the PDA, YHK or coalescent model, but select the birth-death model instead. Here, you can still choose how many trees to simulate, whether the tree(s) should be labelled or not, and how many tips should be included; however, the tree will always be rooted and with clock-like branch lengths. You can also specify the birth and death rates, and whether you wish to include extinct lineages (which will be represented by branches that do not arrive to the end of the tree) or not.

An important point is that if the death rate is relatively high enough, it might be very unlikely for the tree to grow to the required size (it is even possible for all lineages to go extinct). If this is the case, the simulation process may take a long time.

Finally, as mentioned for the YHK and coalescent models, creating a constrained birth-death tree will cause a bias in the distribution of the sampled topologies.

TreeViewer can create a tree starting from biological data, using the UPGMA and Neighbour-Joining (NJ) algorithms.

The input data can be in the form of a sequence alignment or a distance matrix. When a sequence alignment is used as input data, TreeViewer computes a distance matrix from the sequence alignment, and provides that to the UPGMA or NJ methods. Sequence alignments containing either DNA or protein (amino acid) data are supported; the available methods to compute distance matrices are described in the section below.

Distance matrix computation

Distance matrices can be computed using various different metrics. To describe them, we need a few general definitions:

• Let $A$ and $B$ be two sequences that are being compared.
• $d_{A,B}$ is the computed distance between them.
• $M_{A,B}$ is the number of positions where the two sequences have the same residue (i.e., matches).
• $m_{A,B}$ is the number of positions where the two sequences have different residues (i.e., mismatches). Note that all positions where one or both sequences have a gap are ignored.
• For DNA sequences:
  • $ts_{A,B}$ is the number of positions where there is a transition.
  • $tv_{A,B}$ is the number of positions where there is a transversion.
  • Naturally, $m_{A,B} = ts_{A,B} + tv_{A,B}$.

For DNA sequences, the distance matrix can be computed using four different metrics:

• The Hamming distance (Hamming, 1950):

  d_{A,B} = \frac{m_{A,B}}{m_{A,B} + M_{A,B}}
  

  I.e., simply the proportion of sites that differ between the two sequences.

• The Jukes-Cantor distance (Jukes & Cantor, 1969):

  d_{A,B} = -\frac{3}{4}\ln\left(1 - \frac{4}{3} \frac{m_{A,B}}{m_{A,B} + M_{A,B}} \right)
  

  This distance takes corrects for multiple substitutions at the same site, but all possible residue changes are expected to occur at the same rate.

• The Kimura 1980 (K80) distance (Kimura, 1980):

  d_{A,B} = -\frac{1}{2}\ln\left ( \left ( 1 - 2 \frac{ts_{A,B}}{m_{A,B} + M_{A,B}} - \frac{tv_{A,B}}{m_{A,B} + M_{A,B}} \right) \cdot \sqrt{1 - 2 \frac{tv_{A,B}}{m_{A,B} + M_{A,B}} }\right)
  

  With this metric, transitions (i.e., state changes from a purine to a purine, or from a pyrimidine to a pyrimidine) are allowed to happen at a different rate than transversions (i.e., state changes from a purine to a pyrimidine or vice versa).

• The General Time Reversible (GTR) distance (Rodríguez et al., 1990), which uses some matrix manipulations to compute a distance metric that allows all transitions to happen at different rates. Computing this distance is significantly slower than the other distance metrics, but this should not be too relevant in practice.

  Note that the numerical approximations used to compute this distance may occasionally fail (especially with very divergent sequences); if this happens, TreeViewer will show a warning and ask you to select an alternative distance metric.

For protein (amino acid) sequences, the distance matrix can also be computed using four different metrics:

• The Hamming distance (same as for DNA):

  d_{A,B} = \frac{m_{A,B}}{m_{A,B} + M_{A,B}}
  

• The Jukes-Cantor distance (also the same as for DNA, but changing some factors to account for the fact that there are 20 possible amino acids, rather than 4 nucleotides):

  d_{A,B} = -\frac{19}{20}\ln\left(1 - \frac{20}{19} \frac{m_{A,B}}{m_{A,B} + M_{A,B}} \right)
  

• The Kimura 1983 (K83) distance (Kimura, 1983):

  d_{A,B} = -\ln \left ( 1 - \frac{m_{A,B}}{m_{A,B} + M_{A,B}} - \frac{1}{5} \left ( \frac{m_{A,B}}{m_{A,B} + M_{A,B}} \right )^2 \right )
  

  This is used where $\frac{m_{A,B}}{m_{A,B} + M_{A,B}} < \frac{3}{4}$; for higher values, the distances are extracted from a pre-computed table which I extracted from the source code for RapidNJ (Simonsen et al., 2008), though I am not entirely sure where they got them. This distance is supposed to approximate PAM distance.

• The Scoredist correction with BLOSUM62 matrix, which uses the BLOSUM62 matrix to compute protein distances according to the method described by Sonnhammer & Hollich, 2005.

When you select a sequence alignment file as input data to build a tree, TreeViewer automatically detects whether it is a DNA or protein alignment and presents you with the relevant options to compute the distance matrix.

The Neighbor-Joining (NJ) algorithm produces unrooted phylogenetic trees (Saitou & Nei, 1987). A detailed description of this algorithm is beyond this document, but see the reference for more details. Two important points about the neighbour-joining algorithm are:

• If the distance matrix is additive (i.e., for every set of four nodes, there is a way to label them using the letters $i$, $j$, $k$, and $l$, such that $d_{i,j} + d_{l,k} = d_{i,k} + d_{j,l} \geq d_{i,l} + d_{j,k}$), the NJ algorithm is guaranteed to find the tree that induces the distance matrix.
• In some cases (especially when the distance matrix is "far from" being additive), the NJ algorithm may produce branches with negative lengths.

To create a neighbor-joining tree, click on the New item in the File menu, then select Neighbor-joining/UPGMA tree and make sure that Neighbor-joining is selected. You now need to decide whether you wish to use a Sequence alignment or a Distance matrix, and provide an input file. If you are using a sequence aligmment, you also need to specify the metric used to compute the distance matrix and whether you want to compute bootstrap replicates.

Bootstrap is performed by creating the specified number of new alignments, each of which is generated by randomly resampling the columns of the original alignment. Then, these alignments are used to compute new distance matrices, and each distance matrix is used to build a tree. Finally, every split on the original tree is annotated with the proportion of bootstrap trees in which it appears.

The input sequence alignment file can be either in FASTA format, or in relaxed PHYLIP format.

As mentioned above, NJ can in some instances produce a tree with negative branch lengths. You can prevent this by deselecting the box Allow negative branch lengths; when you do this, branches with negative length will have their length set to 0, while the remaining length is added to the sibling branch.

You can also apply a constraint to the tree building algorithm. At every step in the NJ algorithm, this will cause the program to check whether the new candidate split is compatible with the constraint tree and to discard it if it is not. Note that this will increase significantly the amount of time required to build a tree (and may worsen the negative-branches issue).

Once you are satisfied with the settings, click on the Create tree button to create the NJ tree. The tree(s) will open in TreeViewer and you can work on it as usual (including e.g. saving it as a Newick file from with the Save item from the File menu). If you have applied a constraint while creating the tree, the backbone corresponding to the constraint will be highlighted in the new tree.

The UPGMA algorithm produces rooted clock-like trees (Sokal & Michener, 1958). You can find a nice description of this algorithm here: http://www.slimsuite.unsw.edu.au/teaching/upgma/.

To build a UPGMA tree in TreeViewer, you can follow the same steps as for a Neighbor-Joining tree, but selecting the UPGMA algorithm instead. In this case, negative branch lengths are not produced by the algorithm, hence there is no option to correct them. UPGMA trees can also be constrained or bootstrapped.

Harding, E. F. (1971). The probabilities of rooted tree-shapes generated by random bifurcation. Advances in Applied Probability, 3(1), 44–77. https://doi.org/10.2307/1426329

Kingman, J. F. C. (1982). The coalescent. Stochastic Processes and Their Applications, 13(3), 235–248. https://doi.org/10.1016/0304-4149(82)90011-4

Hamming, R. W. (1950). Error Detecting and Error Correcting Codes. Bell System Technical Journal, 29(2), 147–160. https://doi.org/10.1002/J.1538-7305.1950.TB00463.X

Jukes, T. H., & Cantor, C. R. (1969). Evolution of Protein Molecules. Mammalian Protein Metabolism, 21–132. https://doi.org/10.1016/B978-1-4832-3211-9.50009-7

Kimura, M. (1980). A simple method for estimating evolutionary rates of base substitutions through comparative studies of nucleotide sequences. Journal of Molecular Evolution 1980 16:2, 16(2), 111–120. https://doi.org/10.1007/BF01731581

Rodríguez, F., Oliver, J. L., Marín, A., & Medina, J. R. (1990). The general stochastic model of nucleotide substitution. Journal of Theoretical Biology, 142(4), 485–501. https://doi.org/10.1016/S0022-5193(05)80104-3

Kimura, M. (1983). The Neutral Theory of Molecular Evolution. https://doi.org/10.1017/CBO9780511623486

Simonsen, M., Mailund, T., & Pedersen, C. N. S. (2008). Rapid neighbour-joining. Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 5251 LNBI, 113–122. https://doi.org/10.1007/978-3-540-87361-7_10

Sonnhammer, E. L. L., & Hollich, V. (2005). Scoredist: A simple and robust protein sequence distance estimator. BMC Bioinformatics, 6(1), 1–8. https://doi.org/10.1186/1471-2105-6-108

Saitou, N., & Nei, M. (1987). The neighbor-joining method: a new method for reconstructing phylogenetic trees. Molecular Biology and Evolution, 4(4), 406–425. https://doi.org/10.1093/OXFORDJOURNALS.MOLBEV.A040454

Sokal, R. R., & Michener, C. D. (1958). A Statistical Method for Evaluating Systematic Relationships. University of Kansas Scientific Bulletin, 28, 1409–1438.