Number Systems - RetroKoH/S1Fixed GitHub Wiki
When you’re working with assembly files or binary data in a hex editor, it really helps to understand how number systems work. Don’t worry though, it’s not as scary as it sounds! We already use one number system every day: decimal (base 10). Computers don’t use decimal, but knowing how it works makes it easier to understand the systems that computers do use.
Every number system is built on a base. The base tells you how many unique digits the system has.
- Decimal has 10 digits (0–9).
- Binary has 2 digits (0 and 1).
- Hexadecimal has 16 digits (0–9 and A–F).
In every number system, the value of a number comes from multiplying each digit by the base raised to its position (starting from 0 on the right).
Here is the equation: Value * Base^Place
Examples of this will be shown in each section below.
Decimal (Base 10)
The decimal system is the number system we all use every day. It’s how we write both whole numbers (like 11) and fractions (like 8.5).
Decimal is called base 10 because each digit uses one of 10 unique values:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Here’s how counting works in decimal:
- We start at 0 and go up one number at a time.
- Once we reach 9, we’ve run out of single numbers.
- Adding 1 more makes the 9 “roll over” to 0, and we carry 1 to the next place on the left.
- Now that we have a two-digit number
10, we continue onward. - That’s why after 9 comes 10, after 19 comes 20, after 99 comes 100, and so on.
Each digit’s value depends on its position (or place) in the number. The rightmost digit is in the “ones” place, the next is the “tens” place, then “hundreds,” and so on. Mathematically, each place is a power of 10.
Let’s break down the number 4,631 using our equation:
(4 * 10^3) + (6 * 10^2) + (3 * 10^1) + (1 * 10^0)
(4 * 1000) + (6 * 100) + (3 * 10) + (1 * 1)
4000 + 600 + 30 + 1 = 4631
So the number 4,631 is really just a sum of each digit multiplied by its place value. Pretty straightforward, right? Good, because binary and hexadecimal follow the same exact rules, only with different bases.
Binary (Base 2)
The binary system is the language of all computers, old or new, simple or complex.
Binary is called base 2 because it only has two possible digits:
0 and 1.
Each binary digit is called a bit, and you can think of bits like little light switches: on (1) or off (0).
Computers use billions of these on/off switches to store and process information.
Just like decimal uses powers of 10, binary uses powers of 2. Each place in a binary number represents a power of 2, starting from the rightmost digit (place 0). Let's try to break down a small number that I pulled from the Sonic 1 disassembly: %0111 1111. We can ignore the leading zero.
(1 * 2^6) + (1 * 2^5) + (1 * 2^4) + (1 * 2^3) + (1 * 2^2) + (1 * 2^1) + (1 * 2^0)
(1 * 64) + (1 * 32) + (1 * 16) + (1 * 8) + (1 * 4) + (1 * 2) + (1 * 1)
64 + 32 + 16 + 8 + 4 + 2 + 1 = 127
As you can see with just this example, even small binary numbers can become long and difficult to read. But if computers can't read decimal, and we cannot easily read binary, surely there must be a middle ground, right? Yes, there is!
Hexadecimal (Base 16)
The hexadecimal number system (or hex, for short) is the programmer’s middle ground for working with binary.
Hex is called base 16 because each digit uses one of 16 unique values:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Here, the letters represent values beyond 9:
- A = 10
- B = 11
- C = 12
- D = 13
- E = 14
- F = 15
After F, the hex value
10is equal to 16.
Just like decimal uses powers of 10 and binary uses powers of 2, hex uses powers of 16. For example, let’s break down the hex number 2F:
(2 * 16^1) + (F * 16^0)
(2 * 16) + (15 * 1)
32 + 15 = 47
As you can see, 2F in hex = 47 in decimal. Remember that hex character F = 15, hence why we used that number.
Why use Hex?
There are multiple reasons why we use hex in programming:
- Compact: One hex digit equals 4 binary digits:
- Example: 1111₂ = F₁₆ .
- Readable: Instead of writing 11111111₂ , you can just write FF₁₆ .
- both of these values are equal to 255 in decimal.
- Practical: Memory addresses, machine code, and even web colors use hex because it’s short and maps directly to binary.
Here is a real-world example. Open any image editing tool (for example, Paint). Select the color picker, and opt for a custom color. Most apps nowadays will include a hex readout along with the color wheel, that looks something like this: #FF0000. In this case, the first two hex digits are for red (RR), the second pair of digits are for green (GG), and the last two digits are for blue (BB). This means that the color is (255,0,0), or pure red!
You'll see more than your fair share of hex values in S1Fixed, or in any Sonic disassembly for that matter. Hex values will be denoted with a $ symbol like so:
move.w #$64,d0 ; moves 100 to register d0
The # indicates that it is a number, and $ indicates that it is hex. Without $, the computer would think we wanted to move 64 to register d0, instead of 100. That would likely cause problems!
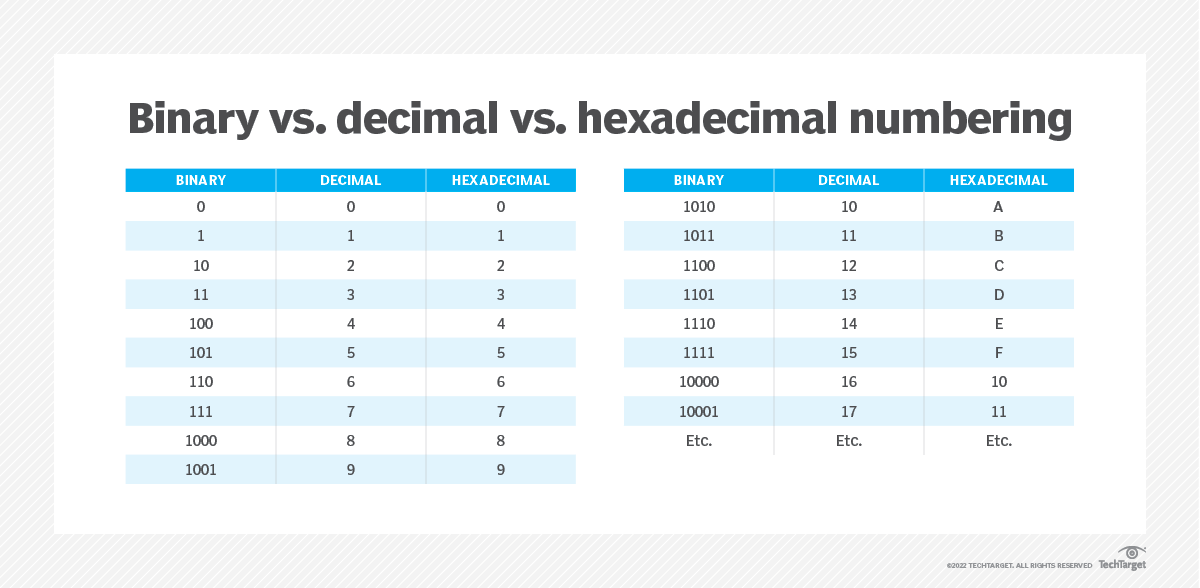
Here is an image reference of the three number systems, and how they relate to one another.
Image Credit: TechTarget