Math for rendering - Fish-In-A-Suit/Conquest GitHub Wiki
Homogenous coordinates
Vectors in 3D are usually considered as an (x, y, z) triplet. However, adding a fourth conponent makes vector math much easier. For rotation, making vectors homogenous makes no difference. For translation, however, it makes life hella easier. This fourth component is known as w.
- If w == 1, then the vector (x,y,z,1) is a position in space
- If w == 0, then the vector (x,y,z,0) is a direction
Note that vectors may represent anything fron colours to the vertices (points) tht define a 3D model. In the case of a model, all vertices (points) are specified locally regarding some point around (or inside) the model, known as the origin/center of the model. Each vertex can then be specified as a vector between the origin and the vertex itself.
Matrices
Matrices are just arrays witg predefined number of rows and columns. In computer graphics, mostly 4x4 (columns×rows) matrices are used so as to transform the (x,y,z,w) vertices. To transform a vertex, multiply that vertex by the matrix. Yes, order matters! matrix x vertex = transformed vertex:
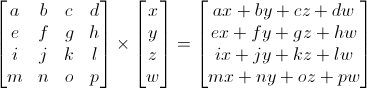
Note that matrices have to be in column-major order for OpenGL to function correctly. Matrix - vector mulutplication works by multiplying each row of a matrix by the column of a vector. The following picture depicts row-major matrix format (above) and a column-major format (below):

In GLSL, the above would be achieved as:
mat4 myMatrix;
vec4 myVector;
// fill myMatrix and myVector somehow
vec4 transformedVector = myMatrix * myVector;
Translation matrices
They are used to move (translate) a vector (vertex/the whole model/the whole world). A translation matrix looks like this:
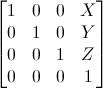
The X, Y and Z are values that you want to add to the current vector. For example, if the player (who is standing at (10, 10, 10, 1)) presses w, you might want to move him 10 units in the x direction, so fill in 10 for X, 0 for Y and 0 for Z. Then, multiply the vector (in this case; it would be the model of the player) with the translation matrix.
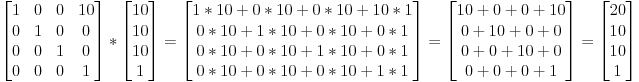
The result is a homogenous vector (20, 10, 10, 1). The transformation didn't change the fact that the vector represents a position, which is good. In the context of the example, the updated player position is (20, 10, 10, 1).
The identity matrix
It doesn't do anything. It's just like multiplying ever vector component by 1:
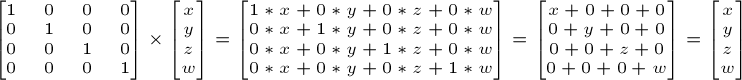
The scaling matrix
The scaling matrix affects both position and direction.
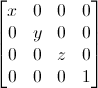
This is an example which would scale a vector (position or direction) by 2 in all directions:
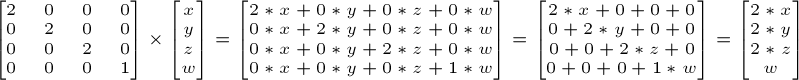
Note: identity matrix is just a speacial case of a scaling matrix, where x, y and z are all 1.
The rotation matrix
Using Euler angles
Euler angles are the easiest way to think of an orientation. You basically store three rotations around the X, Y and Z axes. It’s a very simple concept to grasp. You can use a vec3 to store it: vec3 eulerAngles(rotx, roty, rotz);. These 3 rotations are then applied successively, usually in this order: first Y, then Z, then X (but not necessarily). Using a different order yields different results.
One simple use of Euler angles is setting a character’s orientation. Usually game characters do not rotate on X and Z, only on the vertical axis. Therefore, it’s easier to write, understand and maintain “float direction;” than 3 different orientations. Another good use of Euler angles is an FPS camera: you have one angle for the heading (Y) and one for up/down (X).
When do Euler angles fail?
- smooth interpolation between 2 orientations
- applying several rotations is complicated and unprecise: you have toc ompute the final rotation matrix and guess the Euler angles from this matrix
- Gimbal Lock - an occurence when the roation axis is "lost", therefore blocking rotations --> model is flipped upside down
- different angles make the same rotation (-180 and 180 for instance)
Here are the images for using Euler angles to construct a rotation matrix:
-
rotation around the x axis:

-
rotation around the y axis:

-
rotation around the z axis:

Using quaternions: A quaternion is a set of 4 numbers, [x y z w], which represents rotations the following way:
// RotationAngle is in radians
x = RotationAxis.x * sin(RotationAngle / 2)
y = RotationAxis.y * sin(RotationAngle / 2)
z = RotationAxis.z * sin(RotationAngle / 2)
w = cos(RotationAngle / 2)
RotationAxis is the axis around which you want to make your rotation. RotationAngle is the angle of rotation around that axis.
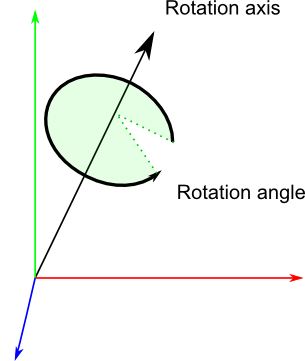
So essentially quaternions store a rotation axis and a rotation angle, in a way that makes combining rotations easy.
This format is definitely less intuitive than Euler angles, but it’s still readable: the xyz components match roughly the rotation axis, and w is the acos of the rotation angle (divided by 2). For instance, imagine that you see the following values in the debugger: [ 0.7 0 0 0.7 ]. x=0.7, it’s bigger than y and z, so you know it’s mostly a rotation around the X axis; and 2*acos(0.7) = 1.59 radians, so it’s a rotation of 90°.
Similarly, [0 0 0 1] (w=1) means that angle = 2*acos(1) = 0, so this is a unit quaternion, which makes no rotation at all.
How to implement matrices in OpenGL
A matrix is represented by 16 floating point numbers (floats), therefore you should create an array of 16 float variables. You can implement functional matrix math in one of two ways: either use row-major-order and perform post-vector multiplication (vector × matrix) or use column-major-order and use pre-vector multiplication (matrix × vector). This is a very important concept so keep this in mind, otherwise GLSL's matrix-vector multiplicarion won't work and you'll end up with odd results.
This is how a float array representing a matrix is created. Matrix elements are represented by letter m and the following number to specify the row and column number where that element is. m01 means matrix element at row 0 and column 1.
public class Matrix4f {
private float matArray = {
m00, m01, m02, m03,
m10, m11, m12, m13,
m20, m21, m22, m23,
m30, m31, m32, m33
}
}
Say, for example, that you want to implement a translation matrix. A translation matrix looks like this:
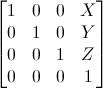
X, Y and Z represent the values for which we want to translate something (vector/whole model) in the x, y and z axes. respectively. For row-major-ordering, you would set the diagonal of the matrix to 1 (m00, m11, m22, m33), and the upper-left three elements to x, y and z: (m03 = x, m13 = y, m23 = z). All other elements are to be set to 0. If we take a look at the elements in the array mat for row-major-order translation matrix: {1, 0, 0, x, 0, 1, 0, y, 0, 0, 1, z, 0, 0, 0, 1} (notice that elements are ordered by increasing index in the matrix array). The translations in the x, y and z axis must be set to 4th (index 3), 8th (index 7) and 12th (index 11) elements in the array.
Now, comes the confusion. Many sources on the internet show the above image and say it is the column-major matrix for translation. This had me confused as well. When starting out with matrix math, I would just compare my float array representing the matrix and then copy the corresponding values from the image, say of a translation matrix directly into my mat array. This led me to implememt a row-order matrix, thinking that it was column-order, since I didn't know that all OpenGL cares about is at which indexes in the array matrix elements are found. Take a look at the above photo where row-major and column-major ordering are presented. You'll see that in the case of a column-major matrix, the red arrow (which indicates how matrix elements should be red) goes down rather than horizontally. This means that you have to set matrix elements to different indexes in the mat array in comparison to row-order matrix. In the case of a translation matrix, the x, y and z translations need to be stored at the 12th, 13th and 14th index:
1 0 0 0
0 1 0 0
0 0 1 0
X Y Z 1
So, to implememt a column-order translation matrix, you must set m30 = x, m31 = y and m32 = z.
Computing the determinant of a 4x4 matrix
There are several different ways of computing a 4x4 matrix, such as:
- block-diagonal approximations
- Laplace (cofactor) expansion
- Leibniz formula for determinants
- principal minors of inverses
- sparse inverse approximations
Computing the inverse of a matrix
The most efficient way of computing a matrix inverse is by using a process called Gauss-Jordan elimination. If A is an n × n square matrix, then one can use row reduction to compute its inverse matrix, if it exists. First, the n × n identity matrix is augmented to the right of A, forming an n × 2n block matrix [A | I]. Now through application of elementary row operations, find the reduced echelon form of this n × 2n matrix. The matrix A is invertible if and only if the left block can be reduced to the identity matrix I; in this case the right block of the final matrix is A−1. If the algorithm is unable to reduce the left block to I, then A is not invertible.
Take a look here for how to compute matrix inverse: https://github.com/LWJGL/lwjgl/blob/master/src/java/org/lwjgl/util/vector/Matrix4f.java