In the real world, we see things because they reflect light from a light source or because they are light sources themselves. In computer graphics, just as in real life, we won’t be able to see an object unless it is illuminated by or emits light (or at least, they will appear 2D). However, real-world lighting is way too complex to be simulated by a computer, at least not in real time. Therefore, we are forced to use approximations in order to simulate real-world as realistic as possible in real time. Lighting computations should be performed on the GPU (fragment and vertex shader).

This is a 3D model, which is not lit by any light source:

Lighting models

Classic lighting model (Blinn-Phong model)

This lighting model adds up a set of independently computed lighting components to get a total lighting effect for a particučar spot on a material surface. These components are ambient, diffuse and specular.

• ambient lighting: objects are almost never completely dark (even when it is dark there is usually still some light somewhere, such as a moon, for example). To simulate this we use ambient lighting constant that always gives objects some colour.
• diffuse lighting: simulates the directional impact a light has on an object. This is the most visually significant component of the lighting model, since the more a part of an object faces a light source, the brighter it becopmes.
• specular lighting: simulates the bright spot of a light that appears on shiny objeccts. Specular highlights are often more inclined to the colour of the light than the colour of the object (for example, if a purple light shines on a white shiny surface, the surface appears purple). Do note, however, that this lighting component is not used in flat shading technique (low-poly style, where each face has the same colour).

Ambient light

Light usually does not come from a single light source, but from many light sources scattered all around us, even when they're not immediately visible. One of the properties of light is that it can scatter and bounce in many directions reaching spots that aren't in its direct vicinity; light can thus reflect on other surfaces and have an indirect impact on the lighting of an object. Algorithms that take this into consideration are called global illumination algorithms, but these are memory-expensive and/or complicated.

To avoid such expensive algorithms, a very simplistic model of global illumination can be used - ambient lighting. This can be implemented quite simply, by adding a constant (ambientConstant) to the fragment shader and then multiply the final output colour of a fragment by this constant:

#version 330

in vec2 outTexCoord;
layout (location = 0) out vec4 fragColour;

uniform sampler2D texture_sampler;
uniform vec3 colour;
uniform int useColour;

float ambientConstant;

void main() {
  
    ambientConstant = 0.2f;
    
	if (useColour == 1) {
	    fragColour = ambientConstant * vec4(colour, 1);
	} else {
	    fragColour = ambientConstant * texture(texture_sampler, outTexCoord);
    }
}

Ambient lighting by itself doesn't add the most interesting results, since a 3D model still looks 2Dish. For example, by using ambientConstant of 0.2f in the above fragment shader, the pine tree model would be rendered as:

Diffuse lighting

Diffuse lighting component of the classic lighting model adds significant visual realism to 3D models, since faces of models which are closer (and facing) a light source appear brighter than faces that are farther (or turned) away from the light source.

To implement diffuse lighting, two vectors are needed: a normal vector of a vertex and a vector from a vertex to the source of the light (called directed light ray). Then, the diffuse lighting constant (which ranges from 0 to 1) is found by dotting these two vectors (which have to be normalized!).

When calculating lighting we usually do not care about the magnitude of a vector or their position; we only care about their direction. Because we only care about their direction almost all the calculations are done with unit vectors since it simplifies most calculations (like the dot product). So when doing lighting calculations, make sure you always normalize the relevant vectors to ensure they're actual unit vectors. Forgetting to normalize a vector is a popular mistake.

If these two vectors are completely parallel (ie, a vertex is facing the light source directly), then their dot product is 1, which is the brightest value for the diffuse component. If these two vectors are perpendicular, then their dot product is 0, which is the darkest value for the diffuse component.

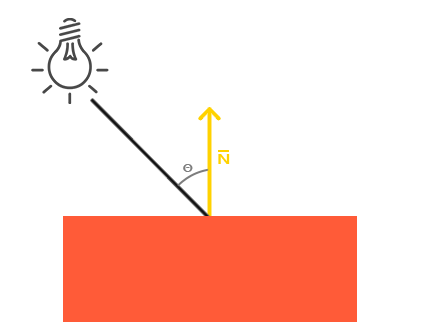
But what if the angle between these two vectors is more than 90 degrees? If the angle is greater than 90 degrees, then diffuse component becomes negative. Since diffuse component can only range from 0 to 1, GLSL built-in float max(float x, float y) method is used, with diffuse component being passed as first parameter and 0.0f as second parameter. This method returns the highest of both of its parameters. Therefore, if a diffuse component is less than 0.0f, max method will clamp it to 0.0f.