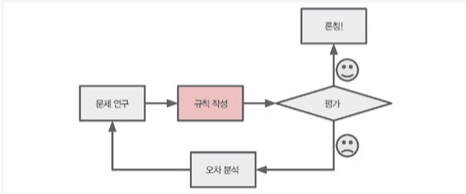
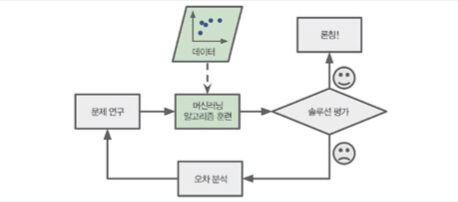
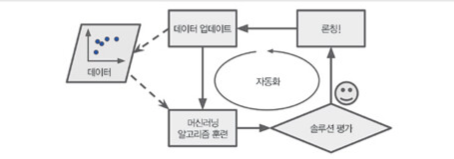
Hand On Machine Learning with Scikit Learn, Keras & TensorFlow PART I 정리 - yarak001/machine_learning_common GitHub Wiki
- Data에서부터 학습하도록 computer를 programming하는 과학(또는 예술)
- "어떤 작업T에 대해 computer의 성능을 P로 측정했을 때 경험 E로 인해 성능이 향상됐다면, 이 computer program은 작업 T와 성능 P에 대한 경험 E로 학습한 것이다" (Tom Michell, 1997)
- 전통적인 접근 방법
- Machine learning 접근 방법
- Program이 훨씬 짧아지고 유시 보수하기 쉬우며, 정확도가 전통적인 방법보다 높음
- Program이 훨씬 짧아지고 유시 보수하기 쉬우며, 정확도가 전통적인 방법보다 높음
- 자동으로 변화에 적응함
- Machine learning을 통해 배울 수 있음
- Data mining: Machine learning 기술을 적용해서 대용량의 data를 분석해 겉으로 보이지 않은 pattern을 발견하는 것
- Data mining: Machine learning 기술을 적용해서 대용량의 data를 분석해 겉으로 보이지 않은 pattern을 발견하는 것
- 사람의 감독하에 훈련하는 것인지 그렇지 않은 것인지(지도, 비지도, 준지도, 강화학습)
- 실시간으로 점진적인 학습을 하는지 아닌지(Online 학습과 batch 학습)
- 단순하게 알고 있는 data point와 새 data point를 비교하는 것인지 아니면 과학자들이 하는 것처럼 훈련 dataset에서 pattern을 발견하는 model을 만드는 것인지(사례기반 학습과 model 기반 학습)
- 학습하는 동안의 감독 형태나 정보량에 따라 분류
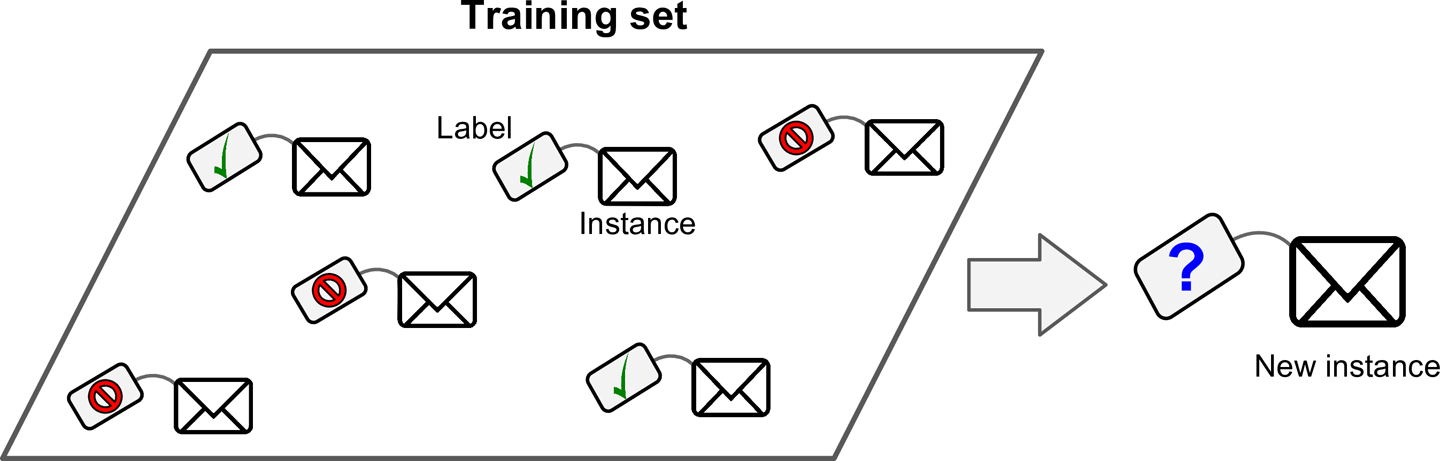
- 지도학습(supervised learning): Algorithm에 주입하는 훈련 data에 label이 포함됨
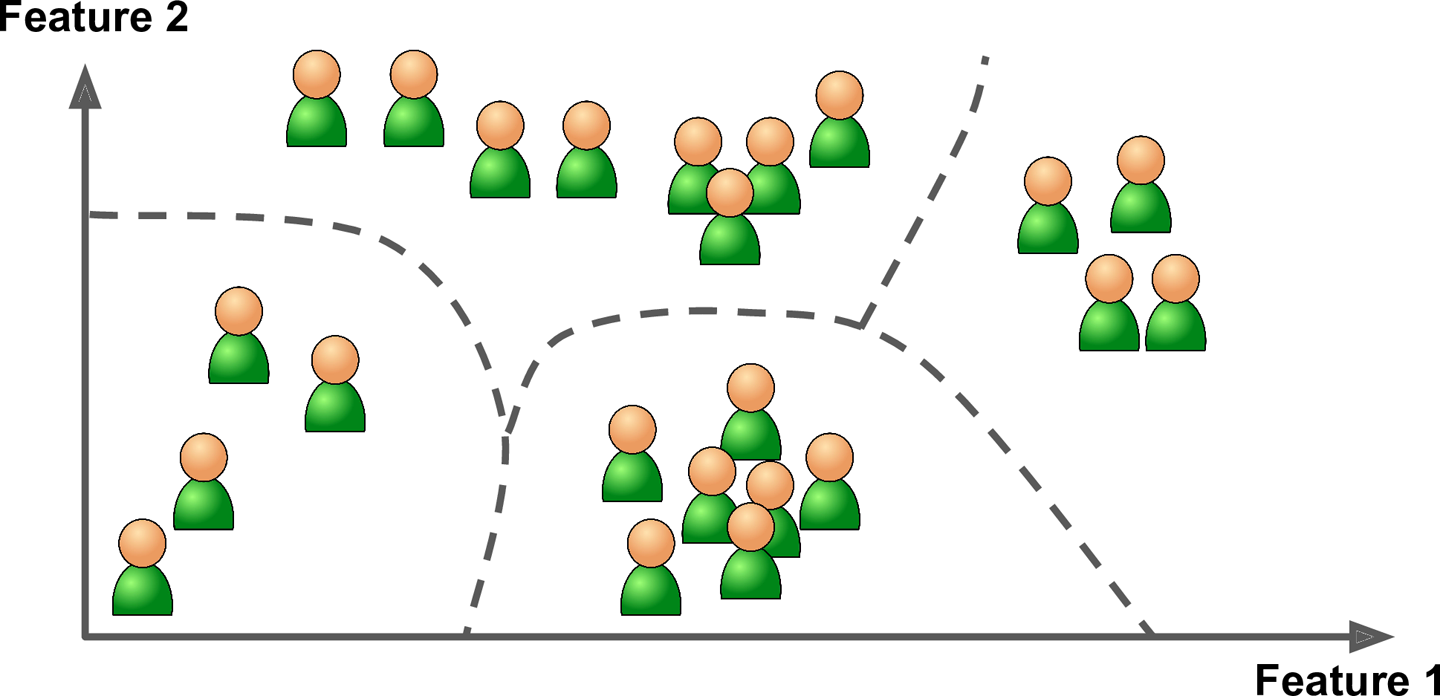
- 분류(classification)
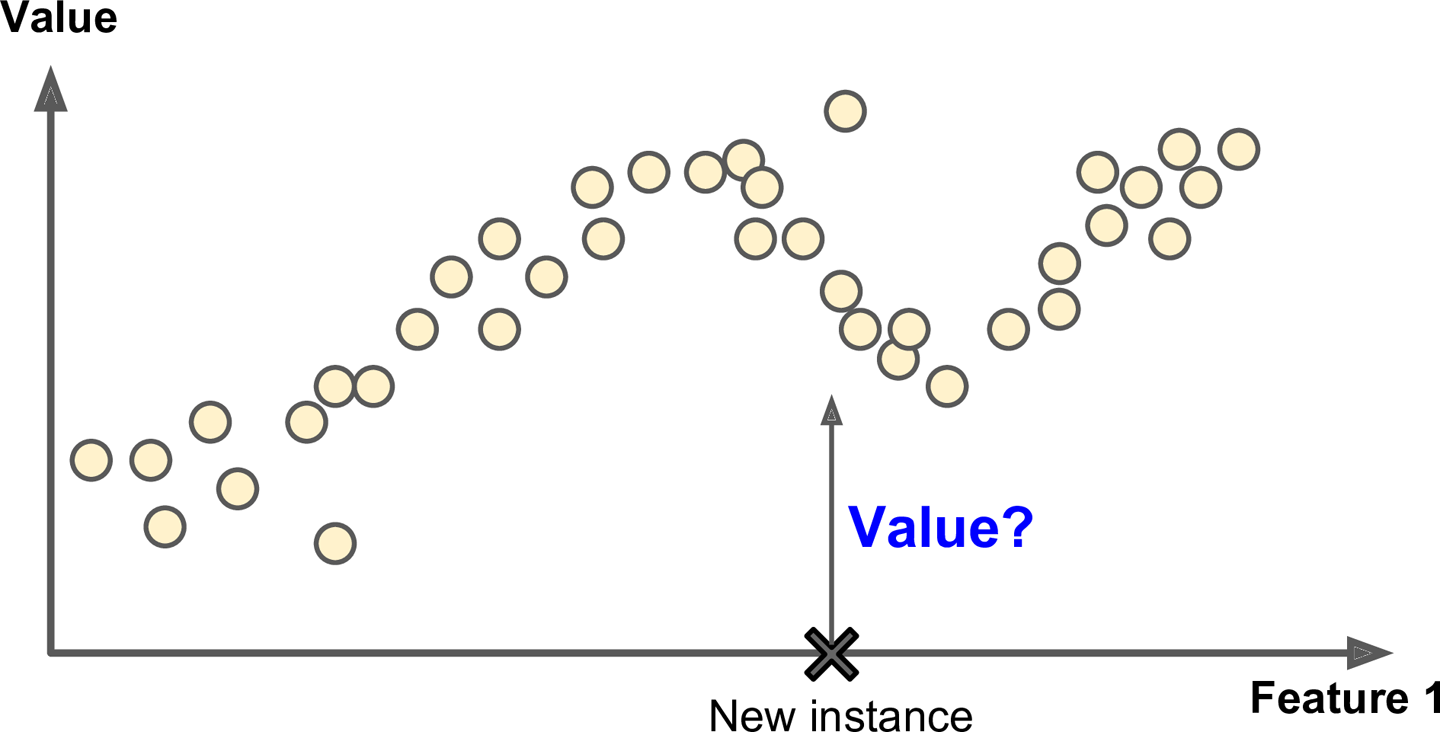
- 회귀(regression): 예측 변수(predict variable)라 부르는 feature(주행거리, 연식, brand등)을 사용해 target(중고자 가격) 수치를 에측하는 것
- 중요한 지도 학습 algorithm
- k-nearest neighbors
- linear regression
- logistic regression
- support vector machine(SVM)
- decision tree, random forest
- neural network
- 분류(classification)
- 비지도 학습(unsupervised learning): 훈련 data에 label이 없음
- 계층군집을 사용하면 group을 더 작은 group으로 나눌 수 있음
- 시각화는 data가 어떻게 조직되어 있는지 이해할 수 있고 예상하지 못한 pattern를 발견할 수 있음
- 차원 축소는 너무 많은 정보를 잃지 않으면서 data를 간소화 함
- 특성 추출
- 지도학습시 data 주입전 사용하면 유용할 수 있음. 실행속도가 빨라지고 disk와 memory 사용량이 줄어들고, 경우에 따라서는 성능이 좋아지기도 함
- 이상치 탐지, 특이치 탐지
- 연관 규칙 학습: 대량의 data에서 특성 간의 흥미로운 관계를 찾는 것
- 중요한 비지도학습 algorithm
- 군집(clustering)
- k-means
- DBSCAN
- 계층 군집 분석(hierarchial cluster analysis, HCA)
- 이상치 탐지(outlier detection)와 특이지 탐지(novelity detection)
- one-class SVM
- isolation forest
- 시각화(visualization) and 차원축소(dimensionality reduction)
- 주성분 분석(pricipal component analysis, PCA)
- kernel PCA
- 지역적 선형 embedding(locally-linear embedding, LLE)
- t-SNE(t-distributed stochastic neighbor embedding)
- 연관 규칙 학습(association rule learning)
- Apriori
- Eclat
- 군집(clustering)
- 계층군집을 사용하면 group을 더 작은 group으로 나눌 수 있음
- 지도학습(supervised learning): Algorithm에 주입하는 훈련 data에 label이 포함됨
- 준지도 학습(semisupervised learning)
- 시간, 비용문제로 label이 된 data보다 label이 없은 data가 많음 이른 일부 label이 있는 data를 다룰 때 사용
- 지도 학습과 비지도 학습을 조합으로 이루어짐
- 심층 신뢰 신경망(DBN, deep belief network)는 여러 겹으로 쌓은 제한된 볼츠만 머신(RBM, restricted Bolzmann machine)라는 비지도 학습에 기초함
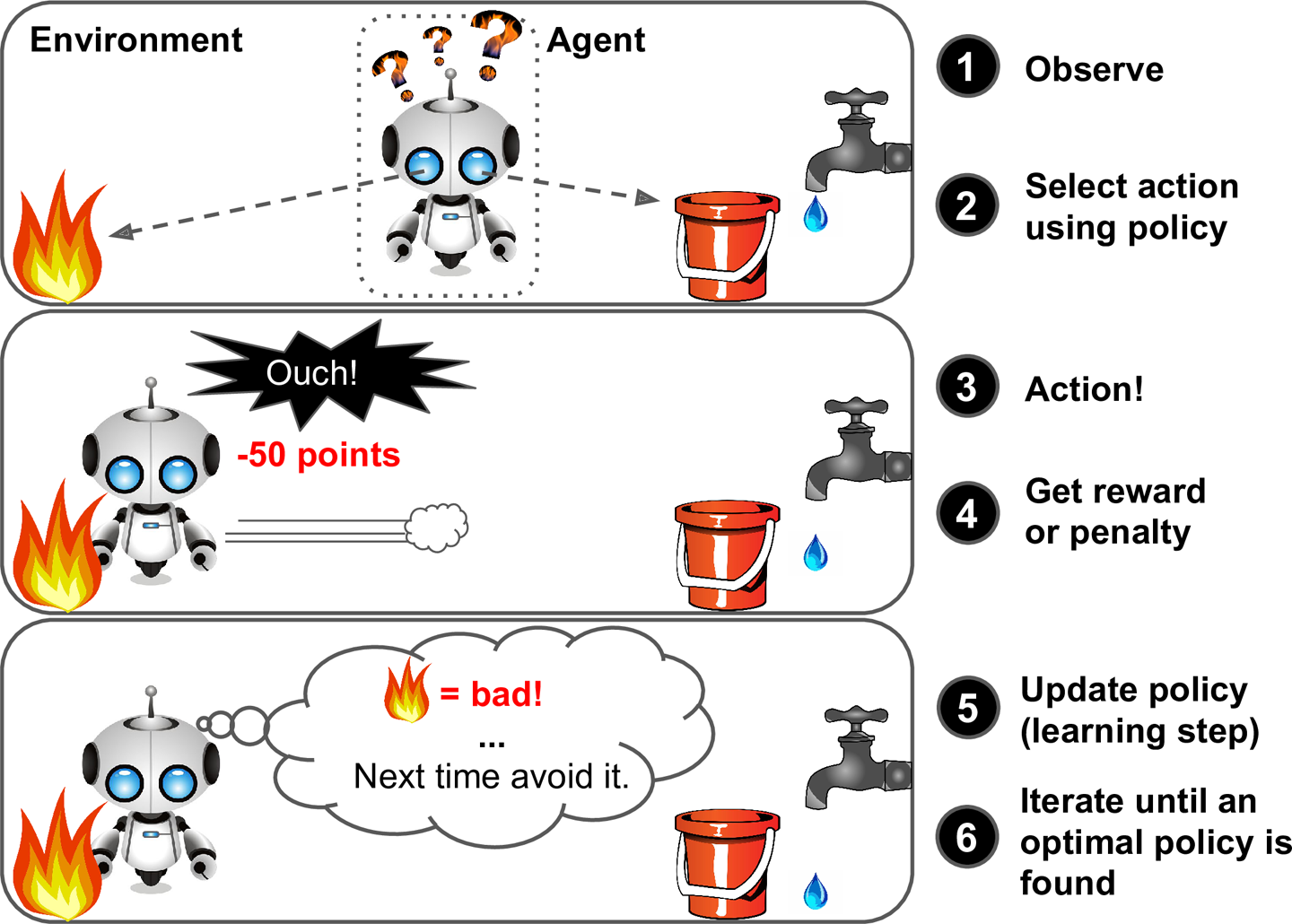
- 강화학습(reinforcement learning)
- 매우 다른 종류의 algorithm
- agent: 학습 system
- 환경을 관찰해서 행동을 실행하고 그 결과로 보상 또는 벌점을 받음
- 시간이 지나면서 가장 큰 보상을 얻기 위해 정책이라고 부르는 최상의 전략을 스스로 학습
- 입력 data stream으로부터 점진적으로 학습할 수 있는지 여부
- Batch 학습
- 가용한 data를 모두 사용하여 훈련
- 시간과 자원이 많이 소요되므로 보통 offline에서 수행됨
- Offline 학습: 먼저 system을 훈련하고 제품을 적용하여 실행. 학습한 것을 단지 적용만 함
- Online 학습
- data를 순차적으로 한 개씩 또는 mini batch라 부르는 작은 묶음 단위로 주입하여 훈련
- 매 학습 단계가 빠르고 비용이 적게 듦
- 연속적으로 data를 받고(ex 주식가격) 빠른 변화에 스스로 적응해야 하는 system에 적합
- 외부 memory(out of core) 학습 or 점진적 학습(increamental learning): computer 한 대의 main memory에 들어갈 수 없는 큰 dataset 학습시 online 학습 algorithm 사용
- system에 나쁜 data가 주입되면 성능이 점진적으로 감소함. system을 면밀히 monitoring하고 성능 감소가 감지되면 즉각 학습 중지 시켜야함(가능하면 이전 system으로 rollback). 이상치 탐지 algorithm으로 입력 data이 비정상 data를 감지하는 것도 방법임
- 어떻게 일반화되는가에 따란 분류
- 주어진 훈련 data로 학습하고 본 적 없는 새로운 data에서 좋은 예측을 만들어야 함(일반화 되어야 함)
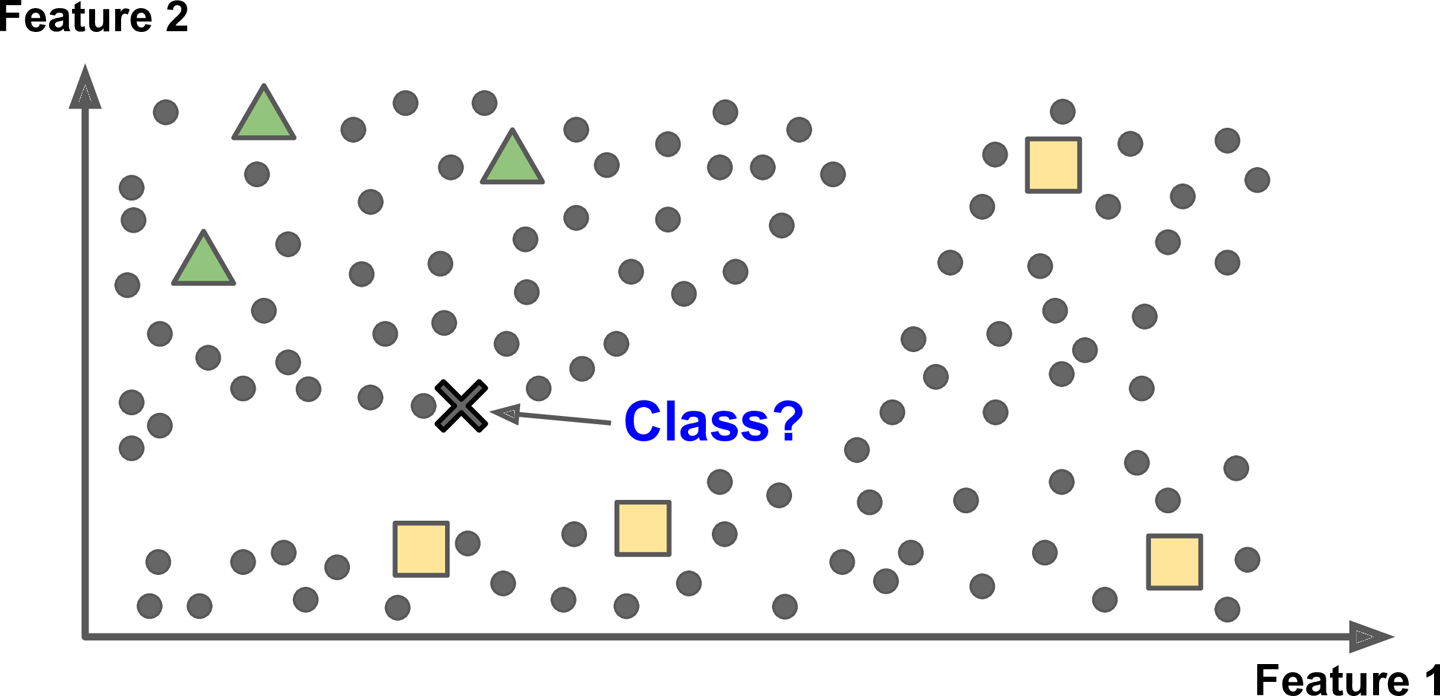
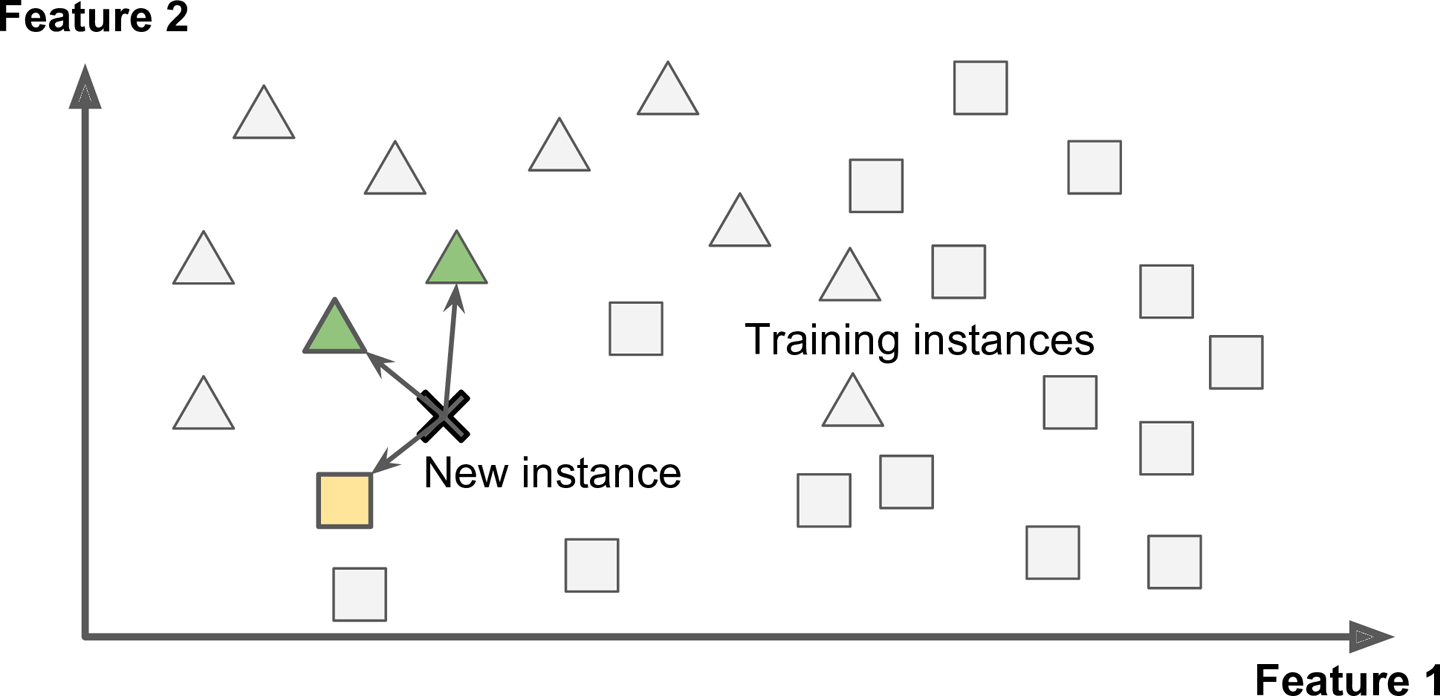
- 사례 기반 학습(instance based learning)
- system이 훈련 sample을 기억함으로서 학습하고 유사도 측정을 사용해 새로운 data와 학습 sample data를 비교하여 일반화 함
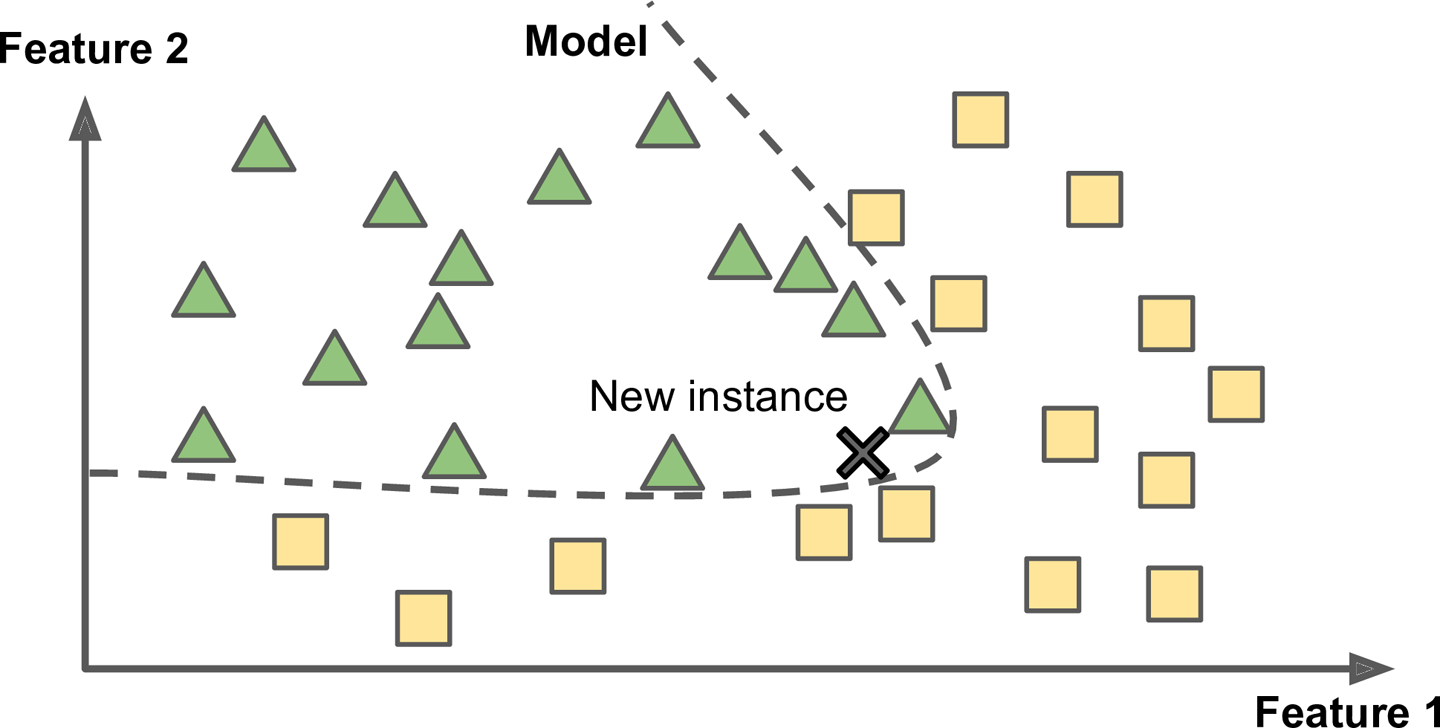
- Model 기반 학습(model based learning)
- Sample들의 model을 만들어 예측
-
- data 분석
-
- model 선택
- 측정 지표
- 효용 함수(utility function) or 적합도 함수(fitness function): 얼마나 좋은지 측정
- 비용 함수(cost function): 얼마나 나쁜지 측정
-
- 훈련 data로 model 훈련
-
- 새로운 data에 model을 적용해 예측(추론)
-
- Sample들의 model을 만들어 예측
- 학습 algorithm을 선택해서 어떤 data에 훈련하는 것이므로 문제가 될 수 있는 것은 나쁜 model과 나쁜 data임
- algorithm이 잘 동작하려면 data가 많아야 함
- 복잡한 문제에서는 algorithm보다 data가 더 중요함. 그렇지만 작거나 중간 규모의 dataset이 여전히 매우 흔하고, 훈련 data를 추가로 모으는 것이 항상 쉽지 않으므로 아직은 algorithm을 무시하지 말아야 함
- 일반화가 잘되려면 일반화하기 원하는 새로운 사례를 훈련 data가 잘 대표해야 함
- Sampling 잡음(sampling noise): 우연에 의한 대표성이 없는 data. sample이 작은 경우 생길 수 있음
- sampling 편향(sampling bias): 표본 추출 방법이 잘못되어 대표성을 띄지 못한 data. sample이 큰 경우 생길 수 있음
- 훈련 data 정제에 시간 투자는 가치가 있음
- 훈련 정제가 필요한 경우
- 명확한 잇아치는 무시하거나 수동으로 수정
- 특성 몇개가 빠졌다면 이를 무시할지, 채울지, 이 특성을 넣은 model과 넣지 않은 model을 별도로 훈련시킬지 결정해야 함
- 엉터리가 들어가며 엉터리가 나온다
- 특성 공학(feature engineering): 성공적인 machine learning project의 핵심 요소는 좋은 특성을 찾는것
- 특성 선택(feature selection): 특성 중 훈련에 유용한 특성 선택
- 특성 추출(feature extraction): 특성을 결합하여 더 유요한 특성을 만듦. 차원 축소 algorithm이 도움이 됨
- 새로운 data를 수집해 특성을 만듦
- 과대적합(overfitting): model이 훈련 data에 너무 잘 맞지만 일반화는 떨어지는 것
- 과대적합은 훈련 data에 있는 잡음의 양에 비해 model이 너무 복잡한 경우 일어남
- parameter수가 적은 model을 선택, 훈련 data의 특성 수를 줄임, model에 제약을 가하거나 단순화 함
- 훈련 data를 더 수집
- 훈련 data에 잡음을 줄임
- 과대적합은 훈련 data에 있는 잡음의 양에 비해 model이 너무 복잡한 경우 일어남
- data에 완벽히 맞추는 것과 일반화를 위해 단순한 model을 유지하는 것 사이에 올바른 균형을 찾는 것이 좋음
- 과소적합(underfitting): model이 너무 단순해서 data의 내재된 구조를 학습하지 못할 때 발생
- model parameter가 더 많은 강력한 model 선택
- 학습 algorithm에 더 좋은 특성 제공(특성 공학)
- model의 제약을 줄임
- machine learning은 기계가 data로부터 학습하여 어떤 작업을 더 잘하도록 만드는 것
- 지도 학습, 비지도 학습, batch 학습, online 학습, 사례 기반 학습, model 기반 학습
- 학습 algorithm이 model 기반이면 훈련 set에 model을 맞추기 위해서 model parameter를 조정하고, 새로운 data에 대해서도 좋을 예측을 만들거라 기대, 사례 기반이면 sample을 기억하는 것이 학습이고 유사도 측정을 사용하여 학습한 sample과 새로운 sample을 비교하는 식으로 일반화
- 엉터리가 들어가며 엉터리가 나옴. 즉 훈련 data가 중요함. 과대적합, 과소적합을 피할 수 있도록 model은 너무 복잡하거나 단순하지 않아야 함
- 훈련 set와 test set
- 훈련 set를사용해 model을 훈련하고 test set를 사용해 model test
- test set에서 model을 평가함으로써 일반화 오차에 대한 추정값을 얻음
- 훈련 오차가 낮지만 일반화 오차가 크다면 이 model은 과대적함임
- 보통 8:2 비율로 분리. 하지만 dataset의 크기에 따라 달라짐
- 일반화 오차를 test set에서 여러 번 측정하면 model과 hyperparameter가 test set에 최적화 될 수 있음 => 새로운 data에 잘 동작하지 않을 수 있음
- holdout 검증: 훈련 set에서 일부를 떼어내 여러 후보 model을 평가하고 가장 좋은 것 선택. holdout set를 검증(validation) set라 함
-
- 훈련 set에서 다양한 hyperparameter를 가진 model 훈련
-
- 검증 set에 가장 높은 성능을 내는 model 선택
-
- (검증 set)를 포함한 전체 훈련 set에 대해 다시 훈련하고 최종 model 생성
-
- 최종 model을 test set에 평가하여 일반화 오차 추정
-
- 교차 검증(cross validation)
- 검증 set와 test set가 실전에서 기대하는 data를 가장 잘 대표해야 함 => 검증 set와 test set에 대표 사진이 배타적으로 포함되어야 함
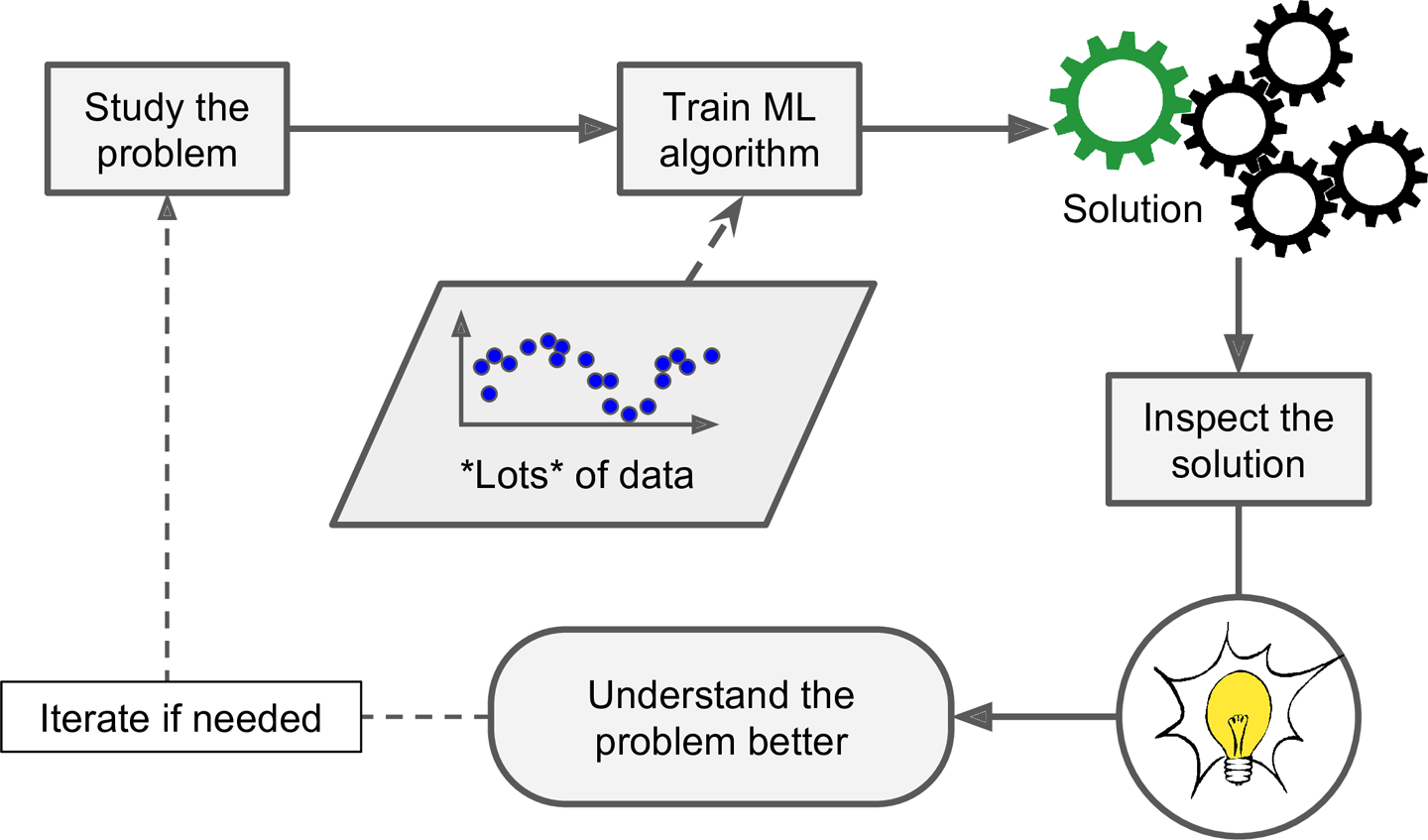
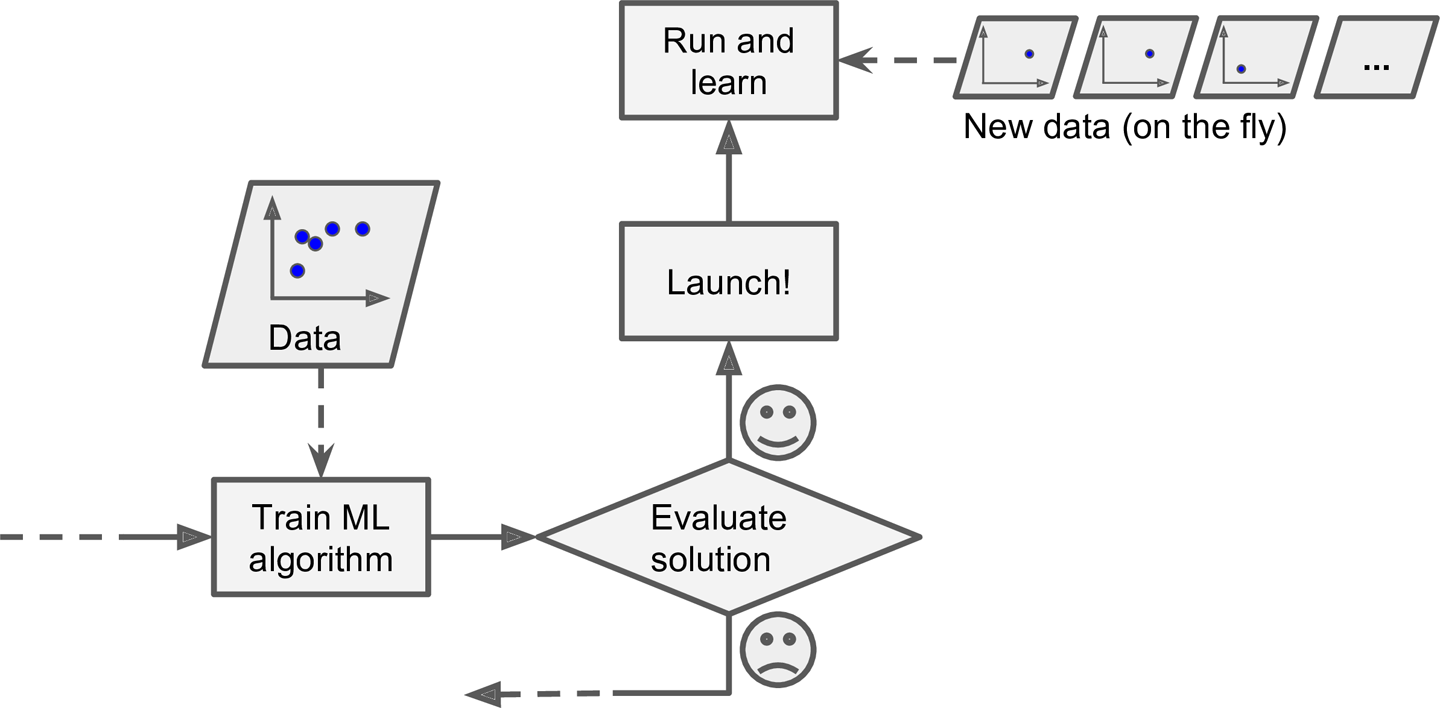
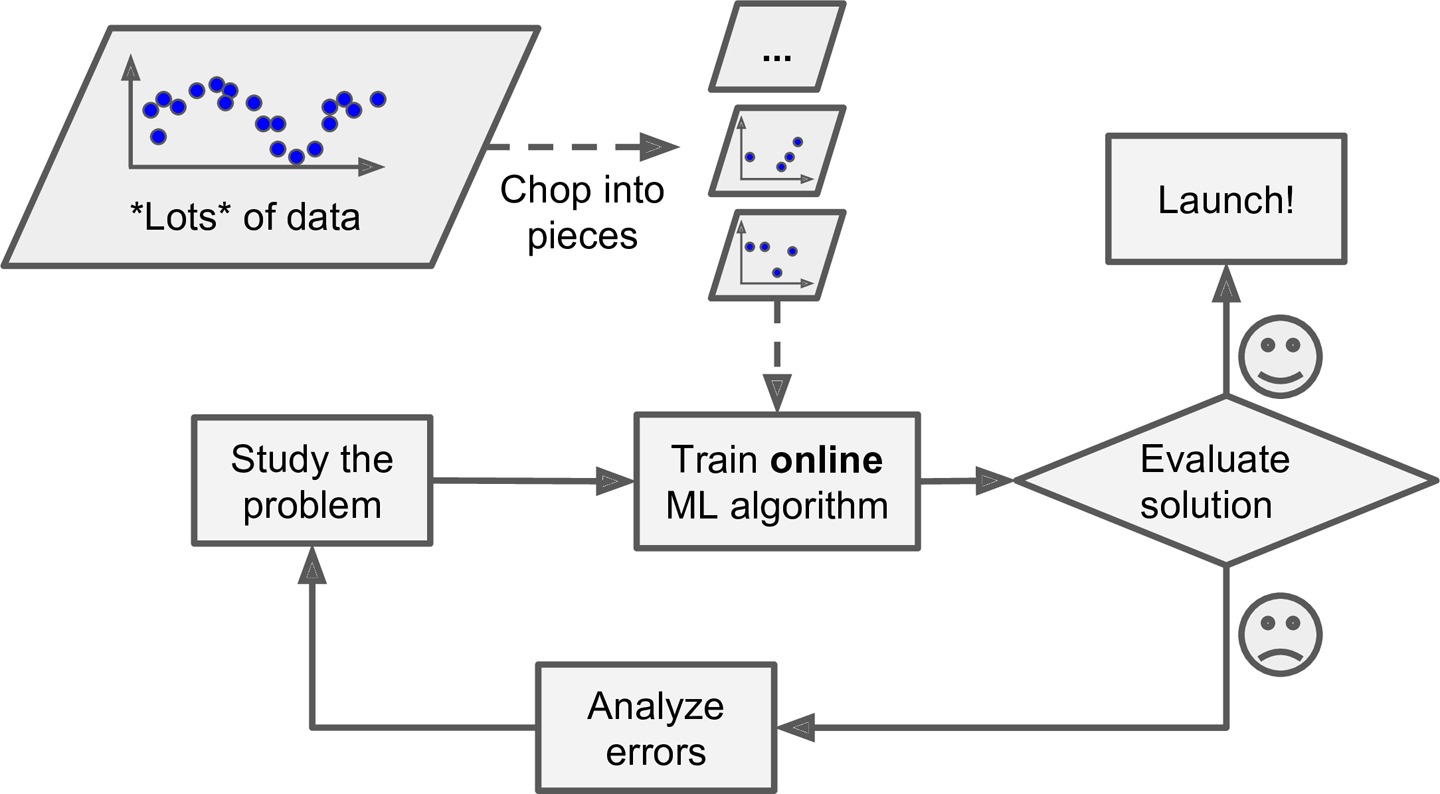
- 큰 그림 보기
- Data 구하기
- Data로부터 통찰을 얻기 위해 탐색하고 시각화
- Machine Learning algorithm을 위해 data 준비
- Model 선택, 훈련
- Model 상세 조정
- Solution 제시
- System launching, monitoring, 유지보수
- Business의 목적이 정확히 무언인가?
- 현재 Solution은 어떻게 구성되어 있나?
- 평균 제곱근 오차(root mean square error, RMSE): 회귀 문제의 전형적인 성능 지표. 오차가 커질수록 지표 값은 더 커지므로 예측에 얼마나 많은 오류가 있는지 가늠케 함
- 평균 절대 오차(mean absolute error, MAE)
- RMSE, MAE는 모두 예측값 vector와 target vector사이의 거리를 재는 방법
- 거리 측정 방법(norm)
- Euclidean norm: RMSE의 계산법, l2 norm
- Mahattan norm: MSE 계산법, l2 norm
- norm 지수가 클수록 큰 값의 원소에 치우치며 작은 값은 무시됨. 그래서 RMSE가 MAE보다 조금더 이상치에 민감. 이상치가 매우 드물면 RMSE가 잘 맞아 일반적으로 널리 사용됨
- 지금까지 만든 가정을 나열하고 검사
- DataFrame.head()
- DataFrame.info()
- Series.value_counts()
- DataFrame.describe()
- 백분위수: 전체 관측값에서 주어진 백분율이 속하는 하위 부분의 값
- DataFrame.hist()
- pandas.cut()
- sklearn.model_selection.StratifiedShuffleSplit
- Data를 더 깊게 들여다보기 전에 test set를 따로 떼어 놓아야 함. 그리고 절대 더 들여다 봐선느 안됨
- Data snooping 편향: test set로 일반화 오차를 추정하면 매우 낙관적인 추정이 되며 system이 launching 했을 때 기대한 성능이 나오지 않는 것
- sklearn.model_selectiong.train_test_split
- 계층적 sampling(Stratified sampling): 계층(strata)라는 동질의 group으로 나누고, test set가 전체 data를 대표하도록 각 계층에서 올바른 수의 sample을 추출
- DataFrame.plot()
- DataFrame.corr(): 표준 상관계수(standard correlation coefficient or Pearson r) 계산
- 1에 까까우면 강한 양의 상관 관계
- -1에 가까우면 강한 음의 상관 관계
- 0에 가까우면 선형적인 상관 관계 없음
- pandas.plotting.scatter_matrix(): 숫자형 특성 사이에 산점도를 그려 상관 관계 조사
- 여러 특성의 조합을 시도
- 함수를 만들어 자동화
- 어떤 dataset에 대해서도 data를 손쉽게 반복
- 향후 project에 사용할 수 있는 변환 library 점진적 구축
- 실제 system에서 algorithm에 새 data를 주입하기 전 변환에 사용
- 여러 data 변환을 시도, 어떤 조합이 가장 좋은지 확인시 편함
- 누락된 특성
- DataFrame.dropna(): 해당 구역을 제거
- DataFrame.drop(): 전체 특성을 삭제
- DataFrame.fillna(): 어떤 값으로 채움(0, 평균, 중간값 등)
- sklearn.impute.SimpleImputer: 누락된 값을 손쉽게 다루도록 해줌
- scikit-learn의 설계 철학
- 일관성: 모든 객체가 일관되고 단순한 interface 제공
- 추정기(estimator)
- dataset기반으로 일련의 model parameter를 추정하는 객체
- 추정 자체는 fit() method에 의해 수행, 하나의 매개변수로 하나의 dataset만 전달(지도 학습 algorithm에서는 매개변수가 두개로, 두번째 매개변수는 label)
- 추정 과정에서 필요한 다른 매개변수들은 모두 hyperparameter로 간주되며, instance 변수로 저장됨
- 변환기(transformer)
- dataset를 변환하는 추정기
- transform()은 dataset을 매개변수로 받안 변환 수행 후 변환된 dataset 반환
- fit_transform(): fit() + transform()
- 예측기(predictor)
- 일부 추정기는 주어진 dataset에 대해 에측 생성
- predict()는 새로운 dataset을 받아 이에 상응하는 예측값 반환
- score()는 test set를 사용해 에측의 품질을 측정
- 검사기능: 모든 추정기의 hyperparameter는 공개(public) instance 변수로 직접 접근 가능. 모든 추정기의 학습된 model parameter도 접미사로 밑줄을 붙여서 공갠 instance 변수로 제공됨
- class 남용 방지: dataset를 numpy 배열이나 scipy 희소행렬로 표현
- 조합성: 기존 구성 요소를 최대한 재사용. Pipeline을 쉽게 만들수 있음
- 합리적인 기본값: 일단 돌아가는 기본 system을 빠르게 만들수 있도록 대부분의 매개변수에 합리적인 기본값 지정해 둠
- 추정기(estimator)
- 일관성: 모든 객체가 일관되고 단순한 interface 제공
- sklearn.preprocessing.OrdinalEncoder
- sklearn.preprocessing.OneHotEncoder
- scikit_learn은 (상속이 아닌) duck typing을 지원하므로 fit()(self를 반환), transform(), fit_transform()를 구현한 python class를 구현하면 됨
- fit_tranform()은 TransformMixin을 상속하면 자동으로 생성
- BeasEstimator를 상속하면(그리고 생성자에 *args나 **kargs를 사용하지 않으면) hyperparameter tuning에 필요한 get_params()와 set_params() 얻음
- machine learning algorithm은 입력 숫자 특성들의 scale이 많이 다르면 잘 작동하지 않음
- target에 대한 scaling을 불필요
- 모든 변환기에서 scaling은 훈련 data에 대해서만 fit()을 적용해야함. 그런 다음 훈련 set와 test set(그리고 새로운 data)에 대해서 transform()을 사용
- min-max scaling (normalization)
- 값이 0~1 범위에 들도록 값을 이동하고 조정
- data에서 최솟값을 뺀 후 최대값과 최소값의 차이로 나눔
- MinMaxScaler
- 표준화(Stradardization)
- 먼저 평균을 뺀 후 표준편차로 나누어 분산이 1이 되도록 함 => 평균이 0 분산이 1
- min-max scaling과 달리 범위의 상한화 하한이 없어 어떤 algorithm에서는 문제가 될 수 있음
- 이상치에 영향을 덜 받음
- StandardScaler
- scikit=learn에서 제공하는 연속된 변환을 순서대로 처리할 수 있게 함
- sklearn.pipeline.Pipeline
- 연속된 단계를 나타내는 이름/추정기 쌍의 목록을 입력.
- 마지막 단계에서는 변환기와 추정기를 모두 사용할 수 있고. 그외는 모두 변환기야 함(fit()과 transform() 또는 fit_transform()을 가져야함)
- Pipelint.fit(): 변환기1의 fit_transform() (or fit() -> transform()) -> 변환기2의 fit_transform() (or fit() -> transform()) -> ... - > 변환기N의 fit_transform() (or fit() -> transform())
- Pipeline 객체는 마지막 추정기와 동일한 method 제공
- sklearn.compose.ColumnTransformer: 하나의 변환기로 각 열마다 적절한 변환 적용하여 모든 열을 처리
- OneHotEncoder는 희소행렬을 반환하지만 ColumnTransfomer는 밀집행렬 반환. 이 둘이 섞여 있을시 ColumnTransformer는 최종 행렬의 밀집정도를 추정하여 임계값(보통 sparce_threshold=0.3)보다 낮으면 희소행렬 반환
- sklearn.linear_model.LinearRegression
- sklearn.metric.mean_squared_error
- sklearn.tree.DecisionTreeRegressor
- scikit-learn의 교차 검증 기능은 scoring 매개변수에 (낮을수록 좋은) 비용함수가 아닌 (높을수록 좋은) 효용함수 기대
- 교차 검증으로 model의 성능을 추정하는 것뿐 아니라 이 추정이 얼마나 정확한지(즉, 표준편차)를 측정할 수 있음
- sklearn.model_selection.cross_val_score
- sklearn.ensemble.RandomForestRegressor
- 여러 종류의 machine learning algorithm으로 hyperparameter 조정에 너무 많은 시간을 들이지 않으면서, 다양한 model을 시도해 봐야함. 가능성 있는 2~5 model 선택이 목적
- sklearn.model_selection.GridSearchCV: 비교적 적은수의 조합을 탐구할 때 사용
- sklearn.model_selection.RandomizedSearchCV: hyperparameter 탐색 공간이 커지만 사용
- 최상의 model을 연결해 보는 것
- System이 특정한 오차를 만들었다면 왜 그런 문제가 생겼는지 이해하고 문제를 해결하는 방법이 무엇인지 찾아야 함
- Test set에서 성능 수치를 좋게 하려고 hyperparameter tuninig을 시도해선 안됨. 이는 새로운 data에 일반환 되기 어려움
- 대부분의 작업은 data 준비 단계, monitoring 도구 구축, 평가 pipeline setting, 주기적 model 학습 자동화로 이뤄짐
- Machine learning algorithm도 중요하지만 전체 process에 익숙해져야 함
- 고수준 algorithm 탐색하느라 시간을 모두 허비해서 전체 process 구축에 충분한 시간을 투자하지 못하는 것보다 서너개의 algorithm만으로도 전체 process를 올바로 구축하는 편이 더 나음
- scikit-learn에서 읽어들이 dataset의 일반적인 구소
- DESC key: dataset을 설명
- data key: sample이 하나의 행, 특성이 하나의 열로 구성된 배열
- target key: label 배열
- binary classifier: 두 개의 class글 구분
- SGDClassifier
- 확률적 경사 하강법(Stochastic Gradient Descent) 분류기
- 매우 큰 data를 효율적으로 처리. 한번에 하나씩 훈련 data 처리 -> online 학습에 잘 맞음
- sklearn.linear_model.SGDClassifier
- 훈련시 무작위성 사용(그래서 확률적). 결과를 재현하고 싶다면 random_state 매개변수 지정
- 분류의 성능 평가는 회귀보가 어려움
- 사용할 수 있는 성능 지표는 많음
- sklearn.model_selection.cross_val_score
- 예제에서 정확도는 분류기 성능 측정 지표로 선호하지 않은 이유를 보여줌, 불균형한 data를 다룰 때 더욱 그러함
- sklearn.model_selection.cross_val_predict
- 각 test fold에서 얻은 예측값 반한
- 깨끗한 예측: model이 훈련동안 보지 못한 data에 대해 예측함
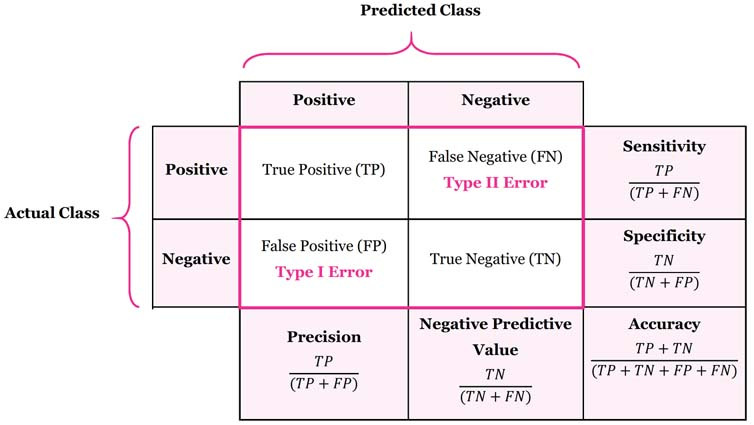
- confusion matrix
- 행: 실제 class, 열: 예측한 class
- 많은 지표 제공
- 정밀도(precision): 양성 예측의 정확도
- 정밀도 = TP / TP + FP
- 재현율(recall) or 민감도(sensitivity) or 진짜양성비율(true positive rate, TPR): 분류기가 정확하기 감지한 양성 sample 비율
- 재현율 = TP / TP + FN
- sklearn.metrics.precision_score
- sklearn.metrics.recall_score
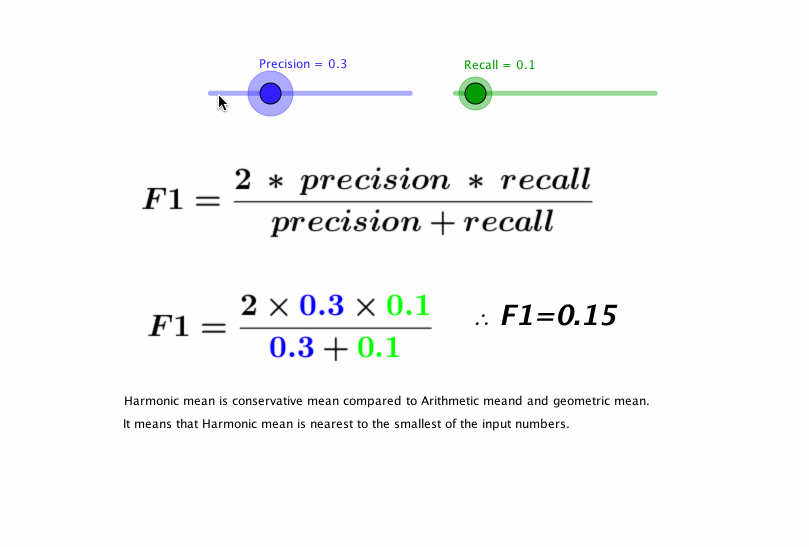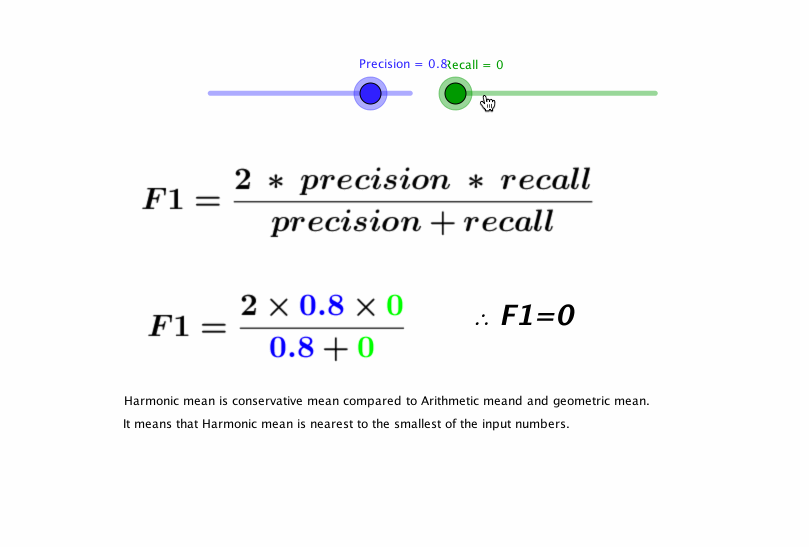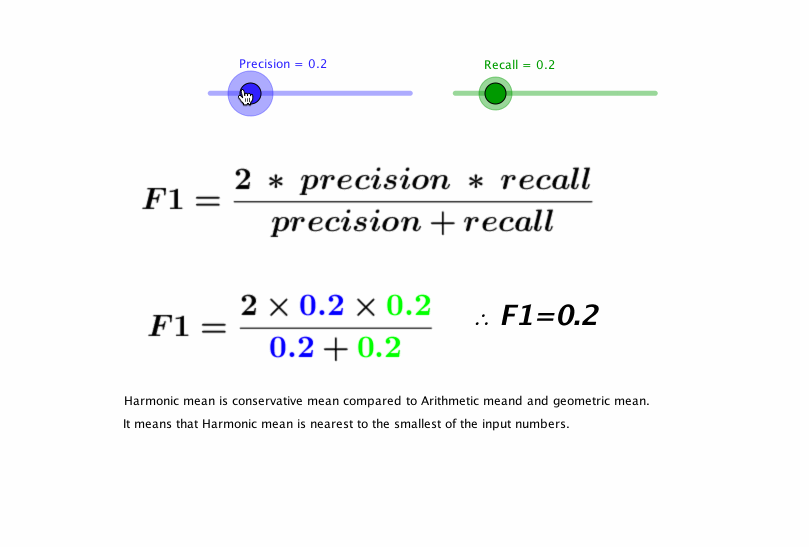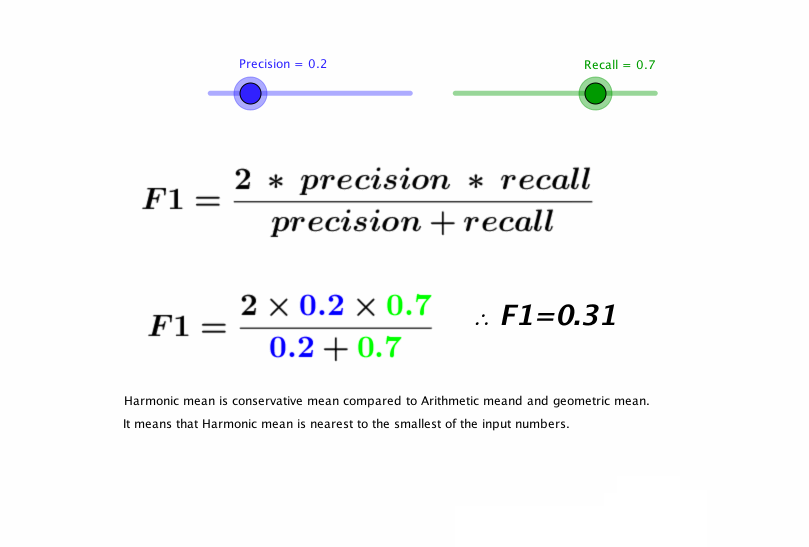
- F1 score
- 정밀도와 재현율을 하나의 숫자로 나타냄
- 두 분류기를 비교할 때 편함
- 정밀도와 재현율의 조화평균(harmonic mean)
- F1 score = 2 * 정밀도 * 재현율 / (정밀도 + 재현율) = TP / (TP + ((FN + FP) / 2))
- sklearn.metric.f1_score
- 정밀도와 재현율이 비슷한 분류기에선는 F1 점수가 높음. 그렇지만 항상 바람직한 것은 아님. 때에 따라서 정밀도가 중요(어린이 content filtering)할 수도 있고, 재현율(감시camera)이 중요할 수도 있음
- 정밀도를 올리면 재현율이 낮아지고 그 반대도 마찬가지 임
- 결정 임계값: 양성 class를 결정하는 기준. 임계값이 보통 임계값이 높으면 재현율이 낮아지고 정밀도는 높아짐
- scikit-learn에서는 임계값을 직접 지정할 수 없음. 분류기에 predict() 대신 decision_function()을 호출하여 각 sample의 점수를 얻을 수 있음
- 적절한 임계값은 어떻게?
- cross_val_predict()를 사용해 훈련set의 모든 sample의 점수를 구함(예측 결과가 아닌 점수를 반환하도록 method="decision_function" 설정)
- 이 점수로 precision_recall_curve()를 사용하여 가능한 모든 임계값에 대한 정밀도와 재현율 계산
- sklearn.metrics.precision_recall_curve
- 재현율에 대한 정밀도 곡것을 그리는 것도 정밀도/재현율 tradeoff를 선택하는 다른 방법임
- 재현율이 너무 낮다면 높은 정밀도의 분류기는 전혀 유용하지 않음 -> 누군가 "99% 정밀도를 달성하자"라고 하면 반드시 "재현율 얼마에서?"라고 물어야 함
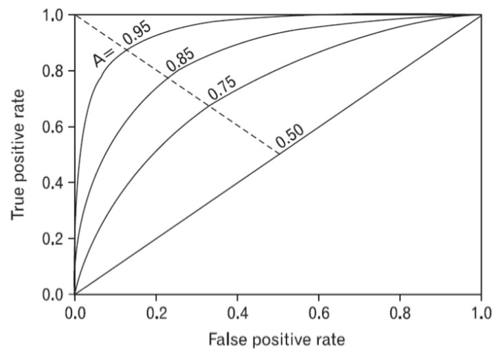
- 수신기 조작 특성(receiver operating characteristic, ROC) 곡선
- 정밀도/재현율 곡선과 매우 비슷(그렇지만 다름)
- 거짓 양성 비율(false positive rate, FPR)에 대한 진짜 양성 비율(true positive rate, TPR) 곡선
- FPR: 양성으로 잘못 분류된 음성 sample 비율 = 1-진짜 음성 비율(true negative rate, TNR)
- TNR을 특이도(specificity)라 함
- ROC 곡선은 민감도(재현율)에 대한 1-특이도 graph
- sklearn.metrics.roc_curve
- 곡선 아래 면적(area under curve, AUC)
- 분류기들 비교시 사용할 수 있음
- 완벽한 분류기는 ROC의 AUC가 1이고, 완전한 random 분류기는 0.5
- sklearn.metrics.roc_auc_score
- 양성 class가 드물거나 거짓 음성보다 거짓 양성보다 거짓 양성이 더 중요할때 PR곡선 사용 그렇지 않으면 ROC곡선 사용
- ROC curve
- ROC곡선 vs. PR곡선
- 다중 분류기(multiclass classifier) or 다항 분류기(multinomial classifier): 둘 이상의 class 구분
- 일부 algorithm은 여러 개의 class를 직접처리하지만 다른 algorithm은 이진 분류만 가능한 것이 있음
- 이진 분류기를 여러 개 사용해서 다중 class를 분류하는 기법도 많음
- OvR(One versus the Rest) or OvA(One versus All) 전략
- 0
9 숫자 image 분류시 0분류기, 1분류기9분류기까지 만들고 분류시 각 분류기의 결정점수가 높은 class 선택
- 0
- OvO(One versus One) 전략
- 0~9 숫자 image 분류시 0-1분류기, 0-2분류기,..., 8-9분류기등과 같이 각 숫자의 조합으로 이진분류기를 생성
- 장점: 각 분류기의 훈련에 전체 훈련 set중 구별할 class에 해당하는 sample만 필요
- SVM 같이 훈련set의 크기에 민감한 algorithm의 경우 OvO를 선호, 대부분 이진 algorithm에서는 OvR선호
- 다중 class 분류 작업에 이진 분류 algorithm 선택시 scikit-learn algorithm에 따란 자동으로 OvR 또는 OvO를 실행
- scikit-learn에서 OvA나 OvR 사용하도록 강제하려면 OneVsOneClassifier나 OneVsRestClassifier사용(이진 분류기 instance를 만들어 객체 생성시 전달, 심지어 이진 분류기일 필요도 없음)
- sklearn.multiclass.OneVsRestClassifier
- sklearn.multiclass.OneVsOneClassifier
- OvR(One versus the Rest) or OvA(One versus All) 전략
- SDGClassifier나 RandomForestClassifier는 직접 sample을 다중 class로 분류할 수 있어 OvR나 OvO를 적용할 필요없음
- cross_val_predict() -> confusion_matrix() -> matplotlib graph
- 위의 graph에서 주 대각선의 밝기가 어두운 경우 -> sample이 적거나 해당 category가 잘 분류되지 않았다는 뜻
- confusion matrix를 분석하면 분류기 성능 향상에 대한 통찰을 얻을 수 있음
- 여러 개의 이진 꼬리표를 출력하는 분류 system
- sklearn.neighbors.KNeiborsClassifier
- 평가지표는 다양함. 한자기는 각 label의 F1 score를 구한 후 이를 간단하게 평균 점수 계산 f1_score()에 average='macro', 각 label의 가중치가 다른 경우, 개수가 많은 label에 가중치를 둠. 이때는 average='weighted'로 설정
- 다중 label분류에서 한 label이 다중 class가 될 수 있도록 일반화 한 것 (즉, 값을 두개 이상 가질 수 있음)
- 이전 장까지 내부가 어떻게 동작하는지 몰라도 많은 것을 처리할 수 있었음 -> machine leanring algorithm을 blackbox처럼 취급
- 내부 동작을 이해하면 적절한 model과 훈련 algorithm 선정 좋은 hyperparameter를 빠르게 찾을 수 있고, debugging이나 error를 효율적으로 분석할 수 있음
- 비용 함수를 최소화 하는 θ를 찾기 위한 해석적인 방법 -> 결과를 바로 얻을 수 있는 수학공식이 있으며 이를 정규방정식이라 함
- 여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 algorithm
- 기본적인 idea는 비용함수를 최소화하기 위해 반복해서 parameter를 조정
- 학습률(learning rate): 중요 parameter는 경사 하강법step의 크기
- 학습률이 너무 작으면 algorithm이 수렴하기 위해 반복을 많이 진행하므로 시간이 오래 걸림
- 학습률이 너무 크면 골짜기를 가로질러 반대편으로 건너뛰게 되어 이전보다 더 높은 곳으로 올라가 발산할 수 도 있음
- 경사하강법을 사용할때는 반드시 모든 특성이 같은 scale을 갖도록 조정(scikit-learn의 StandardScaler등을 사용)
- 각 model parameter θ에 대한 비용함수의 gradient를 계산시 전체 훈련set에 대해 계산
- 매우 큰 훈련 data에서는 아주 느림
- 매 step에서 한 개의 sample을 무작위로 선택하고 그 하나의 sample에 대한 gradient를 계산
- 속도가 빠르고, 큰 훈련 data에 대해서도 memory 사용량이 적음
- batch 경사 하강법 보다 불안정
- 비용 함수가 매우 불규칙할 때 algorithm이 지역 최소값을 건너뛰도록 도와주므로 확률적 경사 하강법이 batch 경사 하강법보다 전역 최소값을 찾을 가능성이 높음
- 무작위성은 지역 최솟값에서 탈출시키지만 algorithm을 전역 최소값에 다다르지 못하게 할 수 도 있음. 학습 scheduler를 사용
- sklearn.linear_model.SGDRegressor
- Mini-batch라 부르는 임의의 작은 sample set에 대해서 gradient 계산
- 확률적 경사 하강법에 비해 mini-batch 경사 하강법은 행렬 연산에 최적화된 H/W 특히 GPU를 사용해서 성능 향상을 얻을 수 있음
| Algorithm | m이 클때 | 외부 memory 학습 지원 | n이 클때 | hyperparameter 수 | scale 조정 필요 | scikit-learn |
|---|---|---|---|---|---|---|
| 정규방정식 | 빠름 | No | 느림 | 0 | No | N/A |
| SVD | 빠름 | No | 느림 | 0 | No | LinearRegression |
| Batch 경사하강법 | 느림 | Yes | 빠름 | 2 | Yes | SGDRegessor |
| 확률적 경사하강법 | 빠름 | Yes | 빠름 | >=2 | Yes | SGDRegessor |
| Mini-batch경사하강법 | 빠름 | Yes | 빠름 | >=2 | Yes | SGDRegessor |
(m: 훈련 sample수, n: 특성 수)
- 비선형 data를 학습하는데 선형 model을 사용할 수 있음
- 다항회귀(polynomial regression): 각 특성의 거듭제곱을 새로운 특성으로 추가하고, 이 확장된 특성을 포함한 dataset에 선형 model을 훈련시키는 것
- sklearn.preprocessing.PolynomialFeatures
- 얼마나 복잡한 model을 사용할 지 어떻게 결정할 수 있을까? 어덯게 model이 data에 과대적합 or 과소적합되었는지 알 수 있을까?
- 교차 검증 사용: 훈련 data에서 성능이 좋고, 검증data에서 나쁘면 과대적합, 둘다 좋지 않으면 과소적합
- 학습곡선: 훈련set와 검증set의 model성능을 훈련set크기(or 훈련반복)의 함수로 나타냄
- 편향/분산 trade off
- model의 일반화 오차는 세가지 다른 종류의 오차의 합으로 표현할 수 있음
- 편향(bias): 잘못된 가정으로 인한 오차. 편향이 큰 model은 훈련 data에 과소적합될기 쉬움
- 분산(variance): 훈련data에 있는 작은 변동에 model이 과도하게 민감함. 자유도가 높은 model이 높은 분산을 가지기 쉬워 훈련data에 과대적합 되지 쉬움
- 줄일 수 없는 오차(irreducible error): data 자체에 있는 잡음으로 발생.
- Model의 복잡도가 커지면 통상적으로 분산이 커지고 편향이 작아짐. 반대로 model의 복잡도가 줄어들면 편향이 커지고, 분산이 작아짐->trade off
- model의 일반화 오차는 세가지 다른 종류의 오차의 합으로 표현할 수 있음
- 과대적합을 감소시키는 방법. model을 제한한다. 자유도를 줄이면 data에 과대적합되지 더 어려워짐
- 다항 회귀 model에서 규제의 간단한 방법은 다항식의 차수를 감소시키는 것
- 선형회귀 model에서는 보통 model의 가중치를 제한함으로써 규제를 가함
- Ridge 회귀(or Tikhonv 규제): 규제가 추가된 선형회귀 version
- data에 맞추는 것뿐만 아니라 model의 가중치가 가능한 작게 유지되도록 함
- 규제한은 훈련하는 동안에만 비용함수에 추가됨.
- model의 훈련이 끝나면 model의 성능을 규제가 없는 성능 지표로 측정
- Ridge 회귀는 입력 특성의 scale에 민감하기 때문에 수행전 scaling 필요
- sklearn.linear_model.Ridge
- SGDRegressor(penalty='l2')
- Ridge회귀처럼 비용함수에 규제항을 더하지만 l2 norm의 제곱을 2로 나눈것 대신 가중치 vector의 l1 norm사용
- 덜 중요한 특성의 가중치를 제거하려는 특징이 있음(즉, 가중치가 0이 됨) => 자동으로 특성 선택을 하고 희소(sparse) model을 만듦
- sklearn.linear_model.Lasso
- SGDRegressor(penalty='l1')
- Ridge회귀와 Rasso회귀를 절충한 model
- sklearn.liner_model.ElasticNet
- 언제 무엇을 사용
- 기본적으로는 평범한 선형 회귀보다는 규제가 약간 있는 것이 좋음
- Ridge가 기본
- 쓰이는 특성이 몇개 뿐이라고 의심되면 Rasso나 Elastic Net이 좋음
- 특성 수가 훈련 sample수보다 많거나 특성 몇 개가 강하게 연관된 경우 Elastic Net선호
- 반복적인 학습 algorithm을 규제하는 색다른 방법 -> 효과적이고 간단해 '훌륭한 공짜 점심' 이라 불리었음
- Logistic regressio(or Logit regression)은 sample이 특정 class에 속할 확률 추정시 널리 사용.
- 추정 확률이 50%를 넘으면 label이 1인 양성class(positive class), 그렇지 않으면 0인 음성class(negative class)를 예측하는 이진 분류기
- logistic regression model은 입력 특성의 가중치 합을 계산함. 대신 선형 회귀처럼 바로 결과를 출력하지 않고 결과 값의 logistic을 출력
- logistic은 0과 1사이의 값을 출력하는 sigmoid 함수임 σ(t) = 1 / (1+exp-t)
- Logit: logit(p) = log(p / (1-p))로 정의되는 logit함수가 logistic함수(sigmoid)함수의 역함수라는 사실에서 이름을 따옴. 실제로 추정확률 p값의 logit을 계산하면 t값을 얻을 수 있음. logit은 양성 class의 추정 확률과 음성 class 추정확률 사이의 log 비율이므로 log-odds라고도 함.
- 훈련의 목적은 양성 sample에 대해서는 높은 확률을 추정하고, 음성 sample에 대해서는 낮은 확률을 추정하는 parameter vector θ를 찾는 것
- sklearn.linear_model.LogisticRegression
- logistic 회귀 model은 여러 개의 이진 분류기를 훈련시켜 연결하지 않고 multi class를 지원하돌고 일반화 될 수 있음.이를 softmax regression, multinomial logistic regression라고 함
- sample x -> 각 class k에 대한 점수 sk(x)를 계산 -> 계산된 점수에 softmax 함수 적용 -> 각 class의 확률 추정
- softmax회귀 분류기는 한번에 하나의 class만 예측. 즉 multi class임(multi output이 아님)
- 훈련방법: model이 target class에 대해서 높은 확률을(그리고 다른 class에 대해서는 낮은 확률을) 추정하도록 만드는 것이 목적. cross entropy 비용함수 사용. cross entropy는 추정된 class의 확률이 target class에 얼마나 잘 맞는지 측정하는 용도로 종종 사용
- sklearn의 LogisticRegression 사용 ** class가 둘 이상일때는 OvA 전략을 사용하지만, multi_class='mutinomial'로 바꾸면 softmax 회귀를 사용할 수 있음. solver='lbfgs'와 같이 softmax 회귀를 지원하는 algorithm을 지정
- SVM(Support Vector Machine)은 매우 강력하고 선형이나 비선형 분류, 회귀, 이상치 탐색에도 사용하는 다목적 machine learning model, 특히 복잡한 분류 문제에 잘 들어 맞으며 작거나 중간 크기의 dataset에 적합
- Large Margin classification: SVM 분류기를 class사이에 가장 폭이 넓은 도로를 찾는 것을 생각할 수 있음
- Support Vector: 도로 바깥 쪽에 훈련 sample을 추가해도 결정 경계에 전혀 영향이 없고, 도로 경계에 위치한 sample에 의해 전적을 결정되는 sample
- SVM은 특성의 scale에 민감. sklearn의 StandardScaler를 사용하면 결정 경계가 후러신 좋아짐
- Hard Margin Classification: 모든 sample이 도로 바깥쪽으로 올바르게 분류됨. data가 선형적으로 구분될 수 있어야 제대로 동작하며, 이상치에 민감한 두가지 문제가 있음
- Soft Margin Classification: Hard margin classification 문제를 피하기 위해 유연한 model이 필요하며, 도록 폭을 가능한 넓게 유지하는 것과 margin violation사이의 적정한 균형을 잡는 방법. margin viloation는 나쁘므로 일반적으로 낮은 것이 좋음
- sklearn의 SVM model사용시 hyperparameter C를 사용하여 도록 폭을 조절. SVM model이 과적합이라면 C를 줄여 감소시킬 수 있음
- SVM 분류기는 logistic 회귀 분류기와 다르게 class에 대한 확률을 제공하지 않음
- sklearn.svm.LinearSVC
- 비선형 dataset을 다루는 한가지 방법은 (4장에서처럼) 다항 특성과 같은 특성을 추가하는 것
- sklearn.preprocessing.PolynomialFeatures
- 다항식 특성을 추가하는 것은 간단하고, 모든 machine learning algorithm에서 잘 작동
- 낮은 차수의 다항식은 매우 복잡한 dataset를 잘 표현하지 못하고, 높은 차수의 다항식은 굉장히 많은 특성을 추가하므로 model이 느려짐
- SVM을 사용할 때 kernel trick이라는 수학적 기교를 적용할 수 있음
- kernel trick: 실제로는 특성을 추가하지 않으면서 다항식 특성을 많이 추가한 것과 같은 결과를 얻을 수 있음. 어떤 특성도 추가하지 않기 때문에 엄청난 수의 특성 조합이 생기지 않음
- sklearn.svm.SVC(kernel='poly', degree=n, coef0=n, C=n)
- 유사도 함수(similarity function): 각 sample이 특정 landmark와 얼마나 닮았는지 측정
- Gaussian RBF(Radial Basis Function): landmark와 가까우면 1, 멀면 0 내에서 값 변화
- LinearSVC는 선형 SVM를 위한 최적화된 algorithm을 구현한 liblinear library기반
- SVC는 kernel tric algorithm을 구현한 libsvm library 기반
- SVM 분류를 위한 sklearn python class 비교
| Python class | 시간 복잡도 | 외부 memory 학습 지원 | scale 조정 필요성 | kernel trick |
|---|---|---|---|---|
| LinearSVC | O(m x n) | 아니오 | 예 | 아니오 |
| SGDClassifier | O(m x n) | 예 | 예 | 아니오 |
| SVC | O(m^2 x n)~O(m^3 x n) | 아니오 | 예 | 예 |
- 일정한 margin 오류 안에서 두 class 간의 도로 폭이 가능한 한 최대가 되도록 하는 대신, 제한된 margin 오류 안에서 도로 안에 가능한 많은 sample이 포함되도록 학습
- sklearn.svm.LinearSVR
- 비선형 회귀작업을 처리하려면 kernel SVM model 사용
- sklearn.svm.SVR
- SVR과 LinearSVR은 각각 SVC, LinearSVC의 회귀 version
- LinearSVR과 LinearSVC는 필요한 시간이 훈련 set 크기에 비례해 선형적으로 증가, 하지만 SVR, SVC는 훈련 set가 커지면 훨씬 느려짐
- SVM을 이상치 탐지에도 사용할 수 있음
- 분류와 회귀 작업, 다중 출력 작업이 가능한 다재다능한 machine learning algorithm
- 매우 복잡한 dataset학습 간응
- RandomForest의 기본 구성 요소
- sklearn.tree.DecisionTreeClassifier
- sklearn.tree.export_graphviz
- Decision tree의 여러 장점중 하나는 data 전처리가 거의 필요하지 않음. 특성 scaling을 맞추거나 평균을 원점에 맞추거나 하는 작업이 불필요
- root node: depth가 0인 node
- leaf node: 자식 node를 가지지 않은 node
- node
- sample: 적용된 훈련 sample
- value: 각 class에 얼마나 많은 sample이 있는지 알려줌
- gini: 불순도(impurity) 측정. 한 node에 모든 sample이 같은 class에 속해 있으면 gini=0
- sklearn은 이진tree만 만드는 CART algorithm사용. leaf node외 모든 node는 두개의 자식 node를 가짐. ID3 같은 algorithm을 사용하면 둘 이상의 자식 node를 가진 decision tree 생성 가능
- model 해석
- white box model: decision tree와 같이 직관적이며 결정 방식을 이해하기 쉬움
- black box model: Random forest나 신경망처럼 성능이 뛰어나고 예측을 만드는 연산과정을 쉽게 확인할 수 있으나, 왜 그런 예측을 만드지는 쉽게 설명이 어려움
- decision tree는 한 sample이 특정 class k에 속할 확률 추정 가능
- scikit-learn이 Decision tree를 학습하기 위해서 CART(classification and regression tree) algorithm사용
- 훈련 set를 하나의 특성 k의 임계값 tk를 사용해서 두개의 subset으로 나누는 과정 반복. 이 과정은 최대 깊이가 되면 중지하거나 불순도를 줄이는 분할 수를 찾을 수 없을때까지 반복 (다른 몇 개의 매개변수도 중지 조건에 관여)
- k와 tk는 크기에 다른 가중치가 적용된 가장 순순한 subset를 나눌 수 있는 (k, tk) 짝을 찾음
- CATR algorithm은 탐욕적(greedy) algorithm. root node에서 최적을 분할을 찾으며 이어지는 각 단계에서 이 과정을 반복. 현재 단계의 분할이 몇 단계를 거쳐 가장 낮은 불순도로 이어질 수 있을지 없을지를 고려하지 않음. 납득할 만한 훌륭한 solution을 만들어 내지만 최적이 solution을 보장하지 않음
- 불순도를 측정하는 방식
- entropy는 분자의 무질서함을 측정하는 것으로 열역학의 개념. 분자가 안정되고 질서 정연하면 entropy는 0 가까움. machine learning에서도 불순도 측정 방법으로 자주 사용되며 어떤 set가 한 class의 sample만 담고 있다면 entropy가 0임
- gini 불순도와 entropy불순도는 크게 차이는 없어 둘다 비슷한 tree를 만들어 냄. gini 불순도가 조금 더 계산이 빠르므로 기본값으로 좋음
- 다른 tree가 만들어지는 경우 gini불순도가 가장 빈도 높은 class를 한쪽 가지로 고립시키는 경향이 있지만 entropy는 좀더 균형 잡힌 tree를 만듦
- decision tree는 훈련 data에 대한 제약사항이 거의 없음 -> 과적합의 가능성 있음
- nonparameter model: 훈련되기 전에 parameter수가 결정되지 않음. -> model 구조가 data에 맞춰져서 고정되지 않고 자유로움. decision tree
- parameter model: 미리 정의된 model parameter수를 가지므로 자유도가 제한되고 과적합의 위험 줄어듬. 선형 model
- DecisionTreeClassifier 결정 tree 형태를 제한하는 parameter(max로 시작하는 매개변수를 감소시키거나 min으로 시작하는 매개변수를 증가시키면 model 규제가 커짐)
- max_depth
- min_samples_split: 분할되기 위해 node가 가져야 하는 최소 sample수
- min_samples_leaf: leaf node가 가지고 있어야 할 최소 sample수
- min_weight_fraction_leaf: min_samples_leaf와 같지만 가중치가 분여된 전체 sample수에서의 비율
- max_leaf_nodes: leaf node 최대 수
- max_features: 각 node에서 분할에 사용할 특성의 최대 수
- pruning: 제한없이 결정 tree를 훈련시키고 불필요한 node를 제거하는 방법
- sklearn.tree.DecisionTreeRegressor
- 계단 모양의 결정 경계 생성 (모든 분할은 축에 수직) -> 훈련set의 회전에 민감 -> 훈련 data를 더 좋은 방향으로 회전시키는 PCA 기법을 사용해 해결할 수 있음
- 훈련 data의 작은 변화에도 매우 민감함
- RandomForest는 많은 tree에서 만든 예측을 평균하여 이러한 불안정성을 극복
- 대중의 지혜(wisdom of the crowd)
- 일련의 예측기(Ensemble)로부터 에측을 수집하면 가장 좋은 model 하나보다 더 좋은 예측을 얻을 수 있음 -> Ensemble 학습
- Ensemble 방법: Ensemble 학습 algorithm
- Project 마지막에 다다르면 흔히 ensemble 방법을 사용하여 이미 만든 여러 예측기를 연결하여 더 좋은 예측기를 만듦

- hard voting(직접 투표): 각 분류기의 에측을 모아서 가장 많이 선택된 class를 예측. 다수결 투표
- 다수결 투표 분류기가 ensemble에 포함된 개별 분류기 중 가장 뛰어난 것보다도 정확도가 높은 경우가 많음
- Ensemble방법은 예측기가 가능한 한 서로 독립적일 대 최고의 성능 발휘. 다양한 분류기를 얻는 한가지 방법은 각기 른 algorithm으로 학습시키는 것임. 이렇게 하면 매우 다른 종류의 오차를 만들 가능성이 높기 때문에 ensemble model의 정확도를 향상함
- sklearn.ensemble.VotingClassfier
- Soft voting(간접 투표): 모든 분류기가 clas의 확률을 에측할 수 있으면 개별 분류기의 예측을 평균내어 확률이 가장 높은 class 예측. 확률이 높은 투표에 비중을 두기 때문에 hard voting보다 성능이 좋음
- 다양한 분류기를 만드는 다른 방법은 같은 algorithm을 사용하고 훈련set의 subset를 무작위로 구성하여 분류기를 각기 다르게 학습하는 것
- Bagging(Bootstrap aggregation): 훈련set에 중복을 허용하여 sampling (통계학에서 중복을 허용한 resampling을 bootstrapping이라 함)
- Pasting: 중복을 허용하기 않고 sampling
- Bagging과 Pasting에서는 같은 훈련 sample을 여러 개의 예측기에 걸쳐 사용할 수 있음. 하지만 bagging만이 같은 훈련 sample을 여러번 sampilng할 수 있음
- 에측기는 모두 동시에 CPU core나 server에서 병렬로 학습 시킬수 있음. 만찬가지로 예측도 병렬로 가능 -> 이런 확장성으로 bagging과 pasting의 인기가 높음
- sklearn.ensemble.BaggingClassifier, BaggingRegressor
- 기본적으로 bagging을 사용하며 pasting을 사용하려면 객체생성시 bootstrap=False 지정
- BaggingClassifier는 기반이 되는 분류기가 class 확률을 추정할 수 있으면 (즉, predict_prob() 함수가 있으면) hard voting대신 soft voting사용
- bootstrapping은 각 예측기가 학습하는 subset에 다양성을 증가시키므로 bagging이 pasting보다 편향이 조금 더 높지만 다양성을 추가한다는 것은 예측기들의 상관관계를 줄이므로 ensemble의 분산은 감소함
- 전반적으로 bagging이 더 좋은 model을 만드므로 선호함. 자원의 여유가 있다면 교차검증으로 bagging과 pasting을 모두 평가해서 더 나은 쪽은 선택하는 것이 좋음
- Bagging을 사용하면 어떤 sample은 한 예측기를 위해 여러번 sampling되고 어떤 것은 전현 선택되지 않음
- 선택되지 않은 훈련 sample의 나머지를 oob(Out Of Bag) sample이라고 함
- 예측기가 훈련하는 동안 oob sample을 사용하지 않으므로 별도의 검증set를 사용하지 않고 oob sample을 사용해 평가할 수 있음 -> BaggingClassifier의 oop_scroe=True 설정. 평가값은 oob_score_변수에 저장됨. 결정함수 값은 oob_score_function_변수에서 확인
- BagggginClassifier는 max_features, bootstrap_features를 통해 특성 sampling지원 -> 각 예측기는 무작위로 선택한 입력 특성의 일부분을 훈련
- 이 기법은 특히 image와 같은 고차원 dataset를 다룰 때 유용
- Random Patches Method: 특성과 sample을 모두 sampling하는 방법
- Random subspace method:훈련 sample을 모두 사용하고 특성을 sampling하는 것((bootstrap=False and max_samples=1.0) and (bootstrap_features=True and/or max_feature < 1.0))
- 일반적으로 Bagging 방법(or Pasting)을 적용한 decision tree의 ensemble
- sklearn.ensemble.RandomForestClassifier, RandomForestRegressor = BaggingClassifier + DescisionTreeClassifier
- RandomForest는 tree의 node를 분할할 때 전체 특성 중에서 최선의 특성을 찾는 대신 무작위로 선택한 특성 후보 중에서 최적의 특성을 찾는 식으로 무작위서 주입 -> tree를 다양하게 만들고 편향을 손해보는 대신 분산을 낮추어 전체적으로 더 훌륭한 model 생성
- Extremely randomized tree ensemble or Extra-tree: tree를 더욱 무작위하게 만드릭 위해서 (보통의 decision tree처럼) 최적의 임계값을 찾는 대신 후보 특성을 사용해 무작위로 분할한 다음 그중에서 최상의 분할을 선택
- sklearn.ensemble.ExtraTreesClassifier, ExtraTreeRegressor
- Random Forest는 특성의 상대적 중요드를 측정하기 쉽다는 장점이 있음
- feature_importance_
- Boosting(원래 hypotheis boosting): 약한 학습기를 여러 개 연결하여 강한 학습기를 만드는 ensemble 방법
- 앞의 model을 보완해 나가면서 일련의 예측기를 학습시키는 것
- AdaBoost와 Gradiend Boosting이 가장 인기 있음
- 이전 model이 과소적합했던 훈련 sample의 가중치를 더 높임 -> 새로운 예측기는 학습하기 어려운 sample에 점점 더 맞춰지게 됨
- 경사하강법과 비슷한 면이 있음. 경사하강법은 비용 함수를 최소화하기 위해 한 예측기의 model parameter를 조정해가는 반면 AdaBoosting는 점차 좋아지도록 Ensemble에 예측기를 추가함
- 연속된 학습 기법에서 각 예측기는 이전 예측기가 훈련되고 평가된 후에 학습될 수 있기 때문에 병렬화를 할 수 없다는 단점이 있음-> 결국 bagging이나 pasting만큼 확장성인 높지 않음
- sklearn.ensemble.AdaBoostClassifier, AdaBoostRegressor
- AdaBoost처럼 ensemble에 이전까지의 오차를 보정하도록 에측기를 순차적을 추가
- AdaBoost처럼 반복되는 Sample의 가중치를 수정하는 대신 이전 예측기가 만든 잔여 오차(residual error)를 새로운 예측기를 학습
- sklearn.ensemble.GradientBoostingRegressor
- 최적화된 gradient boost 구현으로 XGBoost python library가 유명
- Stacking(Stacked generalization): Ensemble에 속한 모든 예측기의 예측을 취합하는 (hard voting 같은)간단한 함수를 사용하는 대신 취합하는 model을 훈련시킬 수 없을까? 라는 idea에서 출발
- Blender(or Meta learner)
- hold-out방식의 dataset를 사용해 훈련
- scikit-learn은 지원하지 않음
- 많은 특성은 훈련을 느리게 할 뿐 아니라, 좋은 solution을 찾기 어렵게 만듦
- 차원 축소는 훈련 속도를 높이는 것 외에 data 시각화(visualization)에 아주 유용함. -> 차원 수를 둘 또는 셋으로 줄이면 고차원 훈련 set를 하나의 압축된 graph로 그릴 수 있고 군집 같은 시각적인 pattern을 감지해 통찰을 얻을 수 있음
- 차원 축소는 일부 정보가 유실됨 -> 훈련 속도가 빨라질 수 있지만 system의 성능이 조금 나뻐질 수 있음. 또한 작업 pipeline이 조금 더 복잡하게 되고 유지 관리가 어려워 짐 -> 차원 축소를 하기 전에 훈련이 너무 느린지 원본 dataset으로 system을 훈련해봐야함. 어떤 경우에는 훈련 daset의 차원을 축소시키면 잡음이나 불필요한 사항을 걸러내므로 성능을 높일 수 있음
- 고차원의 dataset은 매운 희박할 위험이 있음. 즉, 대부분의 훈련 data가 멀리 떨어져 있음 -> 새로운 훈련 sample과 멀리 떨어져 있을 가능성이 높다는 뜻. (실제로는 훈련data의 차원 수가 커짐에 따른 거리는 기하급수적으로 늘어나게 됨)
- 실전 문제는 훈련 sample이 모든 차원에 걸쳐 균일하게 퍼져 있지 않음
- 결과 적으로 모든 훈련 sample이 고차원 공간 안의 저차원 부분공간(subspace)에 놓여 있음
- 차원 축소에 있어서 언제나 투영이 최선의 방법은 아님 -> Swiss Roll dataset처럼 부분 공간이 뒤틀리거나 휘어 있기도 함 -> 2D manifold의 한 예
- mainfold: 고차원 공간에서 sample을 잘 아우를 수 있는 전체 공간의 부분 집합
- d차원 manifold는 국부적으로 d차원 초평면으로 보일 수 있는 n차원 공간의 일부(d<n). -> swiss roll의 경우 d=2,n=3
- manifold learning: 많은 차원 축소 algorithm이 훈련 sample이 놓여 있는 manifold를 modeling하는 식으로 작동 -> 고차원 dataset이 더 낮은 저차원 manifold에 가깝게 놓인다는 manifold 가정(assumption) 또는 manifold 가설(hypothesis)에 근거함
- manifold 가정은 종종 암묵적으로 다른 가정과 병행됨. 즉 처리해야 할 작업(예를들어 분류나 회귀)이 저자춴의 mainfold 공간에 표현되면 더 간단해질 것이란 가정 -> 이 가정이 항상 유효하진 않음
- model을 훈련시키기 전에 훈련set의 차원을 감소키기면 속도는 빨리지지만 항상 더 낫거나 간단한 solution이 되지 않음. -> 전적으로 dataset에 달림
- PCA(Principal Component Analysis, 주성분 분석): 가장 인기 있는 차원 축소 algorithm
- 먼저 data에 가장 가까운 초평면(hyperplane)을 정의한 다음 여기에 data를 투영
- 투영전 올바른 초평면을 선택해야 함. 다른 방향으로 투영하는 것보다 분산이 최대로 보존되는 축을 선택하는 것이 정보가 가장 적게 손실되므로 합리적 -> 원본 dataset과 투영된 것 사이의 평균 제곱 거리를 최소화하는 축
- PCA는 훈련set에서 분산이 최대인 축을 찾음 -> 첫번째 축에 직교하고 남은 분산을 최대한 보존하는 두번째 축을 찾음 -> 고차춴 dataset에서는 dataset에 있는 차원수만큼 n번째 축을 찾음
- i번째 축을 이 data의 i번째 주성분(PC, Principal Component)라 부름
- 특이값 분해(Singular Value Decomposition, SVD)라는 표준 행령 분해 기술로 훈련set의 주성분을 찾음
- np.linalg.svd()
- PCA는 dataset의 평균을 0라 가정, PCA를 직접 구현하거나 다른 library를 사용한다면 먼저 data를 원점에 맞춰야 함(scikit-learn의 PCA python class는 이작업을 대신 처리)
- 처음 d개의 주성분으로 정의한 초평면에 투영하여 dataset의 차원을 d차원으로 축소
- sklearn.decomposition.PCA
- SVD 분해방법 사용
- explained_variance_ratio_: 주성분의 설명도니 분산의 비율(explained variance ration) 저장. 각 주성분의 축을 따라 있 dataset의 분산비율을 나타냄
- 축소할 차원 수를 임의로 정하기보다는 충분한 분산(예를들어 95%)이 될대까지 더해야할 차원수를 선택하는 것이 간단함
- data 시각화를 위해 차원을 축소하는 경우에는 2개나 3개로 줄이는 것이 일반적
- 차원을 축소하고 난 후에는 훈련set의 크기가 줄어듦 -> algorithm의 속도를 크게 높일 수 있음
- 압축된 dataset에 PCA 투영 변환을 반대로 적용하면 차원을 되돌릴 수 있음. 투영에서 일정량의 정보를 잃었기 때문에 이렇게 해도 원본 dataset을 얻을 수 은 없음. 하지만 원본 data와 매우 비슷
- 재구성 오차(reconstruction error): 원본 data와 재구성된 data(압축 후 복원한 것)사이의 평균 제곱 거리
- PCA.inverse_transform()
- PCA에 svd_solver=randomized -> scikit-laern은 Random PCA라 부르는 확률적 algorithm을 사용해 처음 d개의 주성분에 대한 근사값을 빠르게 찾음(기본값은 auto)
- PCA구현의 문제는 SVD algorithm 실행을 위해 전체 훈련set를 memory에 적재해야함 -> 점진적(Incremental PCA, IPCA)로 해결
- 훈련set를 minibatch로 나눈 뒤 IPCA algorithm에 한번에 하나씩 주입. -> 훈련set의 크기가 클때 유용하고 online PCA를 적용할 수도 있음
- sklearn.decomposition.InceremetalPCA
- 전체 훈련 set를 사용하는 fit()이 아니라 minibatch마다 partial_fit() 호출
- np.memmap(): HDD의 이진 file에 저장된 매우 큰 배열을 memory에 들어 있는 것처럼 다룸. 필요시마다 data를 memory에 적재 -> fit()과 같이 사용할 수 있음
- 차원 축소를 위한 복잡한 비선형 투형을 수행
- 투영된 후에 sample의 군집을 유지하거나 꼬인 manifold를 펴치는데 유용
- sklearn.decomposition.KernalPCA
- kPCA는 비지도 학습이기 때문에 좋은 kernel과 hyperparameter를 선택하기 위한 명확한 성능 측정 기준은 없음
- 차원 축소는 종종 지도 학습의 전처리 단계로 사용되므로 grid 탐색을 사용하여 주어진 문제에서 성능이 가장 좋은 kernel과 hyperparameter를 선택할 수 있음
- 지역 선형 embedding(Locally Linear Embedding, LLE)는 도다른 강력한 비선형 차원축소(nonlinear dimensionality reduction, NLDR) 기술
- 투영에 의존하지 않는 mainfold 학습
- 잡음이 너무 많지 않은 경우 꼬인 manifold를 펼치는데 잘 동작
- sklearn.manifold.LocallyLinearEmbedding
- Random project: Rnadom한 선형 투영을 사용해 data를 저차원 공간으로 투영
- 다차원 scaling(Mutidimensional Scaling, MDS): Sample간의 거리를 보존하면서 차원을 축소
- lsomap: 각 sample을 가장 가까운 이웃과 연결하는 식으로 graph 생성. 다음 sample간의 geodesic distance를 유지하면서 차원 축소
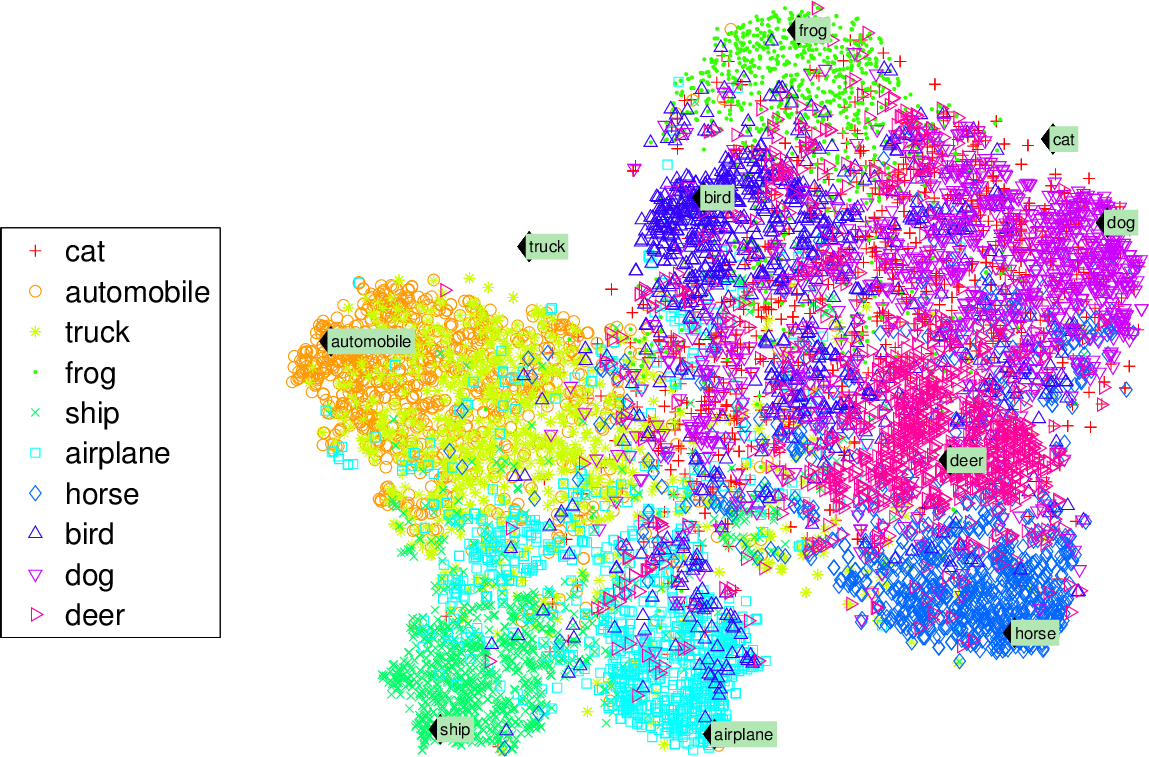
- t-SNE(t-distributed stochastic neighbor embedding): 비슷한 sample은 가까이, 비슷하지 않은 sampleㅇ느 멀리 떨어지도록 하면서 차원 축소, 주로 시각화에 많이 사용되며 특히 고차원 공간에 있는 sample의 군집을 시각화 할때 사용
- 선형 판별 분석(linear discriminant analysis, LDA): 사실 분류 algorithm임. 하지만 훈련 과정에서 class 사이를 가장 잘 구분하는 축을 학습 -> 이 축을 초평면을 정의하는데 사용. 투영을 통해 가능한 한 class를 멀리 떨어지게 유지시키므로 SVM 분류기 가은 다른 분류 algorithm을 적용하기 전에 차원 축소시 유용
- "지능이 케이크라면 비지도 학습은 케이크의 빵이고, 지도학습은 케이크 위의 크림이고, 강화학습은 케이위의 체리"(얀르쿤) => 비지도학습은 큰 잠재력이 있음
- 사람이 label 작업을 할 필요없이 algorith이 label이 없는 data를 바로 사용 -> 비지도 학습
- 8장의 차원축소도 널리 사용되는 비지도학습중 하나
- 군빈(Clustering): 비슷한 sample을 cluster에 모음. 군집은 data분석, 고객분류, 추천system, 검색engine, image분할, 준지도학습, 차원축소드에서 사용
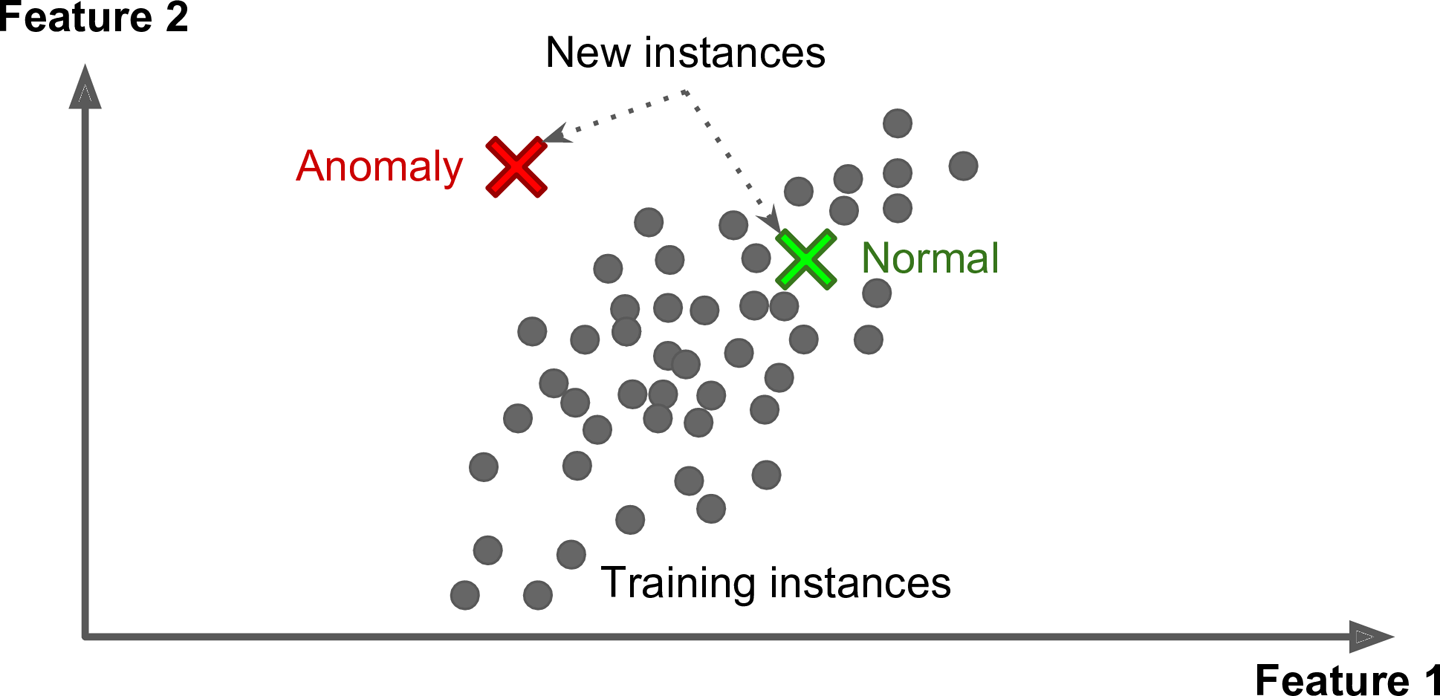
- 이상치 탐지(outlier detection): '정상'data가 어떻게 보이는가를 학습. 그 다음 '비정상' sample을 감지하는데 사용
- 밀도 추정(density estimation): Dataset 생성 확률 과정(random process)의 확률 밀도 함수(Probabiliy Density Function, PDF)추정. 밀도 추정은 이상치 탐지에 널리 사용. 밀도가 매우 낮은 영역에 놓인 sample이 이상치일 가능성이 높음. data분석과 시각화에도 유용
- 군집(Clustering): 비슷한 Sample을 구별해 하나의 cluster 또는 비슷한 sample group에 할당하는 작업
- 각 sample은 하나의 group에 할당됨
- 군집은 활용
- 고객 분류
- Data 분석
- 차원 축소 기법
- 한 dataset에 군집 algorithm을 적용하면 각 cluster에 대한 sample의 친화성 측정 가능.(친화성: sample이 cluster에 얼마나 잘 맞는가?)
- 각 sample의 특성 vector x는 cluster 친화성의 vector로 변환 가능. k개의 cluster가 있다면 이 vector는 k차원이 됨. 이 vector는 원본 특성 vector보다 저차원이지만 분석을 위한 충분한 정보를 가질 수 있음
- 이상치 탐지
- 모든 cluster에서 친화성이 낮은 sample은 이상치일 가능성이 높음
- 준지도 학습
- label된 sample이 적다면 군집을 수행하고 동일한 cluster에 있는 모든 sample에 label 전파
- 이어지는 지도학습 algorithm에 필요한 data를 증식하여 성능을 크게 향상함
- 검색 engine
- DB의 모든 image에 군집 algorithm 적용 -> 사용자 image 입력 -> 훈련된 군집 model을 사용해 image cluster 찾은 후 cluster의 모든 image 반환
- 유사 image 검색
- image 분할
- 색을 기반으로 pixel을 cluster로 구성 -> 각 pixel의 색을 해당 cluter의 평균 색으로 변경
- image에 있는 색상의 종류를 크게 줄여 물체의 윤곽을 감지하기 쉬워져 물체 탐지 및 추적 system에 활용됨
- Cluster에 대한 보편적인 정의는 없음. 상황에 따라 다르며 algorithm이 다른 경우 다른 종류의 cluster를 감지
- 어떤 algorithm은 centroid라 부르는 특정 point를 중심으로 cluster생성
- 어떤 algorithm은 sample이 밀집되어 연속된 영역을 cluster로 생성
- 어떤 algorithm은 계층적으로 cluster 생성
- 반복 몇번으로 dataset를 빠르고 효율적으로 cluster 생성하는 간단한 algorithm
- sklearn.cluster.KMeans
- 이 algorithm은 각 cluster의 중심을 찾고 가장 가까운 cluster에 sample을 할당 KMeans.fit()
- 찾는 cluster개수 k를 지정해야 함 -> k를 정하는 것은 쉬운 일이 아님
- Cluster에서 각 sample의 label은 algorithm이 sample에 할당한 cluster index -> KMeans.slabels_ 변수로 확인
- cluster의 centroid는 KMeans.cluster_centers_로 확인
- 새로운 sample을 가장 가까운 centroid의 cluster에 할당할 수 있음 -> KMeans.predict()
- K-Means는 sample을 cluster에 할당할 때 centroid까지의 거리만을 고려하기 때문에 cluster의 크기가 많이 다르면 잘 동작하지 않음
- hard clustering: sample을 하나의 cluster에 할당, soft clustering: cluster마다 sample에 대한 점수 부여(점수는 centroid와의 거리 또는 유사도 점수, 친화성 점수)
- K-Means algorithm
- centroid를 random하게 생성
- sample에 label을 할당하고 centroid update를 centroid 변환가 없을때까지 반복
- 이 algorithm에서 반복횟수는 제한된 횟수 안에서 수렴함(무한반복하지 않음)
- k-Means는 가장 빠른 clustering algorithm중 하나
- algorithm은 수렴하는 것이 보장되지만 적절한 solution으루 수렴하지 못할 수 있음(즉, 지역 최적점으로 수렴되는 경우) -> centroid초기화에 달림
- centroid 초기화
- (다른 군집 algorithm으로)Centroid 위치를 근사하게 알 수 있다면 KMean()의 init 매개변수에 centroid list를 지정하고, n_init=1로 설정할 수 있음
- 또다른 방법은 Random 초기화 algorithm을 매번 다르게 하여 가자 좋은 solution을 사용 -> random 초기화 횟수는 KMeans()의 n_init로 조정(기본값 10. 이는 KMeans.fit() 내부에서 algorithm이 10번 실행되면 가장 좋은 solution 반환)
- 그렇다면 최선의 solution이라는 것은 어떻게 알 수 있을까?
- 성능 지표인 inertia사용
- inertia: 각 sample과 가장 가까운 centroid와의 평균 제곱 거리
- KMeans class는 algorithm은 n_init번 수행하여 inertia가 가장 낮은 model 반환
- KMeans.inertia_로 확인
- KMeans.score(): inertia의 음수값 반환(예측기의 score()는 "큰 값이 좋은것이다"라는 scikit-learn규칙을 따르기 때문)
- k-Means++ algorithm: 다른 centroid와 거리가 먼 centroid를 선택하는 똑똑한 초기화 기법 소개
- KMeans 초기화 기본법은 k-Means++ algorithm기법. 원래 방식대로 하려면 init="random"으로(거의 사용하지 않음)
- k-Means 속도 개선과 minibatch k-Means
- 속도개선
- 불필요한 거리 계산을 많이 피함으로써 algorithm 속도 개선-> sample과 centroid사이의 거리를 위한 상한선, 하산선 유지 => KMeans class의 기본으로 사용(원래 algorithm을 사용하려면 KMeans()의 algorithm="full" 그렇지만 거의 쓸일 없음)
- minibatch k-Means
- 전체 dataset을 사용하지 않고 각 반복마다 minibatch를 사용해 centroid를 조금씩 이동. 3~4배의 속도개선. memory에 들어가지 않은 대량의 dataset에 적합
- sklearn.cluster.MiniBatchKMeans
- minibatch k-Measn는 일반 k-Means algorithm보다 훨씬 빠르지만 일반적으로 inertia는 (cluter개수 증가시)조금 더 나쁨
- 속도개선
- 최적의 cluster 개수 찾기
- cluster개수 k는 쉽게 알 수 없음
- 제일 작은 inertia를 가진 model을 선택하면 되지 않을까? inertial는 k가 증가함에 따라 점점 작아지므로 k 선택을 위한 좋은 성능 지표는 아님
- elbow: inertia graph를 cluster개수 k로 그렸을 때 graph가 꺾이는 지점 -> k의 선택의 하나의 기준이 될 수 있음. 그렇지만 좀 엉성항
- silhouette score
- elbow 보다 좀더 (계산비용이 많이 들지만)정확한 방법
- silhouette score = 모든 sample의 silhouette coefficient의 평균
- silhouette coefficient(계수)
- (b-a)/max(a,b)
- a: 동일 cluster에 있는 다른 sample까지의 평균거리(즉, cluster내부의 평균거리)
- b: 가장 가까운 cluster까지 평균 거리(즉, 가장 가까운 cluster의 sample까지 평균 거리)
- -1 ~ +1자
- +1: 자신의 cluster안에 잘 속해있고 다른 cluster와는 멀리 떨어짐
- 0: cluster의 경계에 위치
- -1: 잘못된 cluster에 위치함
- (b-a)/max(a,b)
- sklearn.metric.silhouette_score
- silhouette diagram: 모든 sample의 silhouette 계수를 할당된 cluster와 계수값으로 정렬하여 표시
- graph의 높이: cluster가 포함하고 있는 sample수
- graph의 너비: cluster에 포함된 sample의 정렬된 silhouette 계수(넓은수록 좋음)
- 수직 파선: 각 cluster 개수에 해당하는 silhouette score
- 한 cluster의 sample 대부분이 이 점수보다 낮은 계수를 가지면(즉, 많은 sample이 파선의 왼쪽에서 멈추면) cluster sample이 다른 cluster와 너무 가깝다 -> 좋지 않은 cluster
- 장점
- 속도가 빠르고 확장 용이
- 단점
- 최적 solution을 위해 algorithm이 여러 번 실행
- cluster 개수를 지정해야 함
- cluster의 크기나 밀집도가 서로 다른거나 원형이 아닌 경우 잘 동작하지 않음
- k-Means를 실행하기 전에 입력 특성의 scaling을 맞추는 것이 중요. 그렇지 않으면 cluster가 길쭉해지고 k-Means의 결과가 좋지 않음. 특성의 scale을 맞추어도 모든 cluster가 잘 구분되고 원형의 형태를 가진다고 보장할 수 없지만 일반적으로 더 좋아짐
- image 분할(image segmentation): image를 segment 여러 개로 분할하는 작업
- semantic 분할(semantic segmentation): 동일한 종류의 물체에 속한 모든 pixel을 같은 segment에 할당
- cluster는 차원 축소에 효과적. 특히 지도학습 algorithm을 적용하기 전에 전처리 단계로 사용가능
- label이 없는 data가 많고 label이 있는 data가 적은 경우 사용
- label 전파: cluter 대표 sample에 사람이 label을 부여하고 이를 동일 cluster내 sample에 전파
- 밀집된 연속적 직역을 cluster로 변환
- 작동방식
- algorithm이 각 sample에서 작은 거리인 ε내에 sample이 몇개 있는지 count => sample으 ε-negihbor
- (자기 자신을 포함해) ε-neighbor내에 적어도 min_samples개 sample이 있다면 이를 핵심(core) sample로 간주함. 즉 핵심 sample은 밀집된 지역에 있는 sample
- 핵심 sample의 이웃에 있는 모든 sample은 동일한 cluster에 속함. 이웃에 다른 핵심 sample이 포함될 수 있음. 따라서 핵심 sample의 이웃의 이웃은 계속 해서 하나의 cluster 형성
- 핵심 sample이 아니고 이웃도 아닌 sample은 이상치로 판단
- 모든 cluster가 충분히 밀집되어 있고 밀집되지 않은 지역과 잘 구분될 때 좋은 성능 발휘
- sklearn.cluster.DBSCAN
- DBSCAN.labels_: sample의 label확인. -1인 sample은 이상치
- DBSCAN.core_sample_indices: 핵심 sample의 index
- DBSCAN.components_: 핵심 sample 자체
- predict() 제공하지 않고 fit_predict()제공 => 새로운 sample에 대해 cluster를 예측할 수 없음. 다른 분류 algorithm(e.g. sklearn.neighbor.KNeighborsCalssi이 이런 작업을 더 잘 수행할 수 있기 때문임
- 장정
- DBSCAN은 매우 간단하지만 강력한 algorithm. cluster의 모양과 개수에 상관없이 가감지할 수 있는 능력
- 이상치에 안정적이고 hyperparameter가 두개 뿐(eps와 min_sample) -> 사전에 cluster수를 지정할 필요가 없음
- 단점
- cluster간의 밀집도가 크게 다르면 모든 cluster를 올바르게 잡아내는 것은 불가능
- 계산복잡도가 sample개수에 따라 선형적으로 증가