[深度学习]20170921 RNN中的梯度爆炸和梯度消失 - xiaobu1986/Notes GitHub Wiki

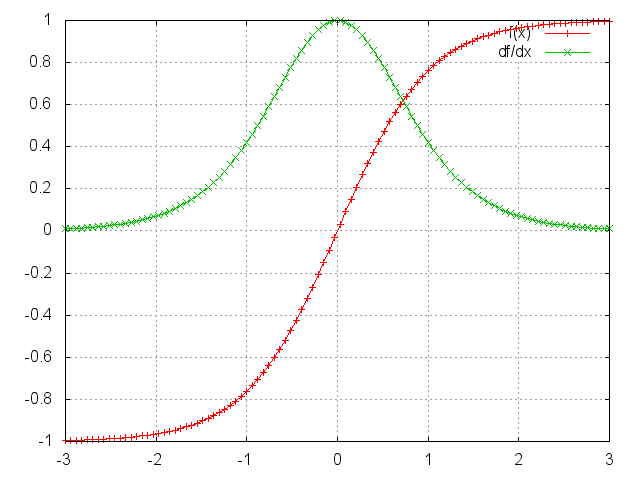
你可以看到tanh和sigmoid函数在两端的梯度值都为0，接近于平行线。当这种情况出现时，我们就认为相应的神经元饱和了。它们的梯度为0使得前面层的梯度也为0。矩阵中存在比较小的值，多个矩阵相乘会使梯度值以指数级速度下降，最终在几步后完全消失。比较远的时刻的梯度值为0，这些时刻的状态对学习过程没有帮助，导致你无法学习到长距离依赖。消失梯度问题不仅出现在RNN中，同样也出现在深度前向神经网中。只是RNN通常比较深（例子中深度和句子长度一致），使得这个问题更加普遍。

梯度消失与梯度爆炸受关注差异性 很容易想到，依赖于我们的激活函数和网络参数，如果Jacobian矩阵中的值太大，会产生梯度爆炸而不是梯度消失问题。梯度消失比梯度爆炸受到了更多的关注有两方面的原因。其一，梯度爆炸容易发现，梯度值会变成NaN，导致程序崩溃。其二，用预定义的阈值裁剪梯度可以简单有效的解决梯度爆炸问题。

梯度消失的解决方法 梯度消失出现的时候不那么明显而且不好处理。1）合适的初始化矩阵W可以减小梯度消失效应，正则化也能起作用。2）选择ReLU而不是sigmoid和tanh作为激活函数。ReLU的导数是常数值0或1，所以不可能会引起梯度消失。3）通用的方案时采用长短项记忆（LSTM）或门限递归单元（GRU）结构。LSTM在1997年第一次提出，可能是目前在NLP上最普遍采用的模型。GRU，2014年第一次提出，是LSTM的简化版本。这两种RNN结构都是为了处理梯度消失问题而设计的，可以有效地学习到长距离依赖，我们会在教程的下一部分进行介绍。