Polar to Cartesian Coordinate Transformation - wtepfenhart/BioSimVis GitHub Wiki

Cartesian coordinates also called rectangular coordinates allow one to specify the location of a point in the plane, or in a 2-D or 3-D space. The commonly known X-Y or X-Y-Z axis.

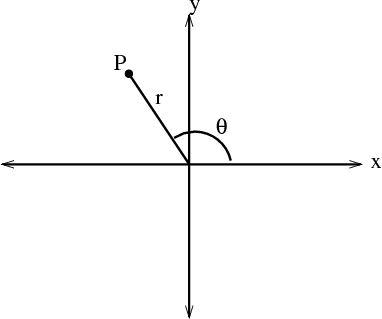
In mathematics, the polar coordinate system is a 2-D coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point is called the pole, and the ray from the pole in the reference direction is the polar axis.

Mapping Polar coordinates to Cartesian coordinates is equivalent to transform T(r,θ) = (x,y) where x = r cosθ and y = sin θ.

x² + y² = r²

tan θ = y / x

cos θ = x / r, hence x = r cos θ

sin θ = y / r, hence y = r sin θ

Following is the proposed formula for to draw the golden spiral as shown in the Phyllotaxis plant.

Where,

• n is the ordering number of a floret, counting outward from the center. This is the reverse of floret age in a real plant.

• φ is the angle between a reference direction and the position vector of the n^th floret in a polar coordinate system originating at the center of the capitulum. It follows that the divergence anglebetween the position vectors of any two successive florets is constant, α = 137.5◦.