CRF Questions - ufal/NPFL095 GitHub Wiki
- (motivational) Consider the example sentence from the previous lecture:
he/N can/V can/V a/N can/N
HMM is a generative model, meaning that it models the join probability P(o,s), so it can generate the most probable tag sequence.
Consider the observation b3 from last lecture?
- Make sure that you understand shortcut notation: P(Yv|X,Yw,w~v) in the definition of CRF in Section 3
Compare the definition, Figure 2 on page 4 and the Figure below.

What is missing in Figure 2 in the paper?
Suppose the CRF above (there are only those 3 Ys).
Express the probability P(Yi-1|X, Yi, Yi+1) for the CRF in Figure above (use the definition).
**Hint:** If you don't understand the shortcut notation, just ignore it and use your intuition (vertices connected by edges are not independent).
-
MEMMs suffer from Label Bias Problem. What about HMMs? Why?
-
Which of the following features are useful? Why?
4a) Xi = "can"
4b) Xi = "can" & Yi = N
4c) Xi = "can" & Yi-1 = N
4d) Xi-1 = "can" & Yi = N & Yi-1 = V
4e) Xi-1 = "can" & Yi = N & Yi+1 = V
4f) Xi-2 = "can" & Yi = V & Yi-1 = N
4g) Xi+3 = "can" & Yi = N & Yi-2 = V
4h) X1 = "The" & Yi-1 = N & Yi = N
4i) Xi has more letters than Xi-1 & Yi = N
4j) X contains word "dog" & (Yi = N or Yi = V) -
CRFs have been specifically designed to overcome the Label Bias Problem. From Figure 2 you may observe that the only difference between CRF and MEMM is that the orientation of edges is discarded. The paper states that "CRFs use the observation-dependent normalization Z(x) for conditional distributions" which is then later described as
and then the notation is not used in the formula below (just to add more confusion to the paper).
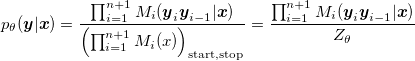
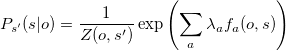
Suppose that MEMM is given observation sequence o1, o2, ... on. Using the formula above write down formula for the probability of the whole tag sequence, that is
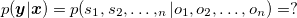
If s = si then s' = s?
-
Compare your formula from the 4th question and the formula from the paper (the first formula in the 4th question).
What is the main difference?
Hint: Notation is different but note that the numerators are quite similar. -
Let's suppose that we have a CRF for the data "he/N can/V can/V a/N can/N" and these features:
f1: Xi = can & Yi = V && (Yi-1 = N || Yi-1 = V)
f2: Xi = can & (Yi = N || Yi = V) & Yi-1 = N
g1: Xi = he & Yi = N
7a) |Y| = ?
7b) Simplify (as much as possible) the
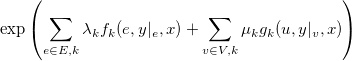
expression in Formula 1, given the above definitions of f1, f2 and g1.
7c) (bonus question) Let's suppose, that λ1=1, λ2=1, μ1=1.
Explain (either in the rigorous math way, or just your own words) why the
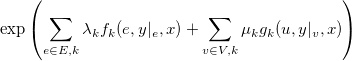
expression in Formula 1 (page 3) and
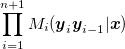
(numerator in the formula on page 4) give the same result.
**Hint:** The alpha-like symbol ∝ means "is directly proportional", i.e. A∝B ⇔ A=k*B & k≠0. See [Wikipedia](http://en.wikipedia.org/wiki/Proportionality_%28mathematics%29#Direct_proportionality).
The vertical bar in "y|v" does not mean conditional probability, see its definition under Formula 1.
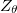 and then the notation is not used in the formula below (just to add more confusion to the paper).
and then the notation is not used in the formula below (just to add more confusion to the paper).