ERPLAB Studio Panels: Measurement Tool - ucdavis/erplab GitHub Wiki
The Measurement Tool is used to measure features of the ERP waveforms, such as amplitudes and latencies.
The basic idea is that you specify a set of ERPsets, a set of bins, a set of channels, and a specific measurement to be performed (e.g., peak latency between 300 and 600 ms), and then the tool performs all of the measurements and saves them in a text file. For example, the settings shown in the screenshot below would measure the latency of the most positive peak between 200 and 400 ms from channels 13, 14, and 21 in bins 3 and 4 from ERPsets 1-6.
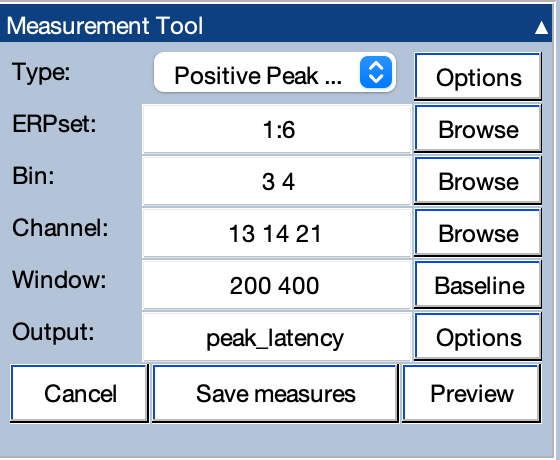
We strongly recommend viewing the measures from the individual ERP waveforms to make sure that you are actually measuring what you want to measure. To do this, click the Preview button. Here's what it looks like for mean amplitude measurements with the parameters shown in the screenshot above.
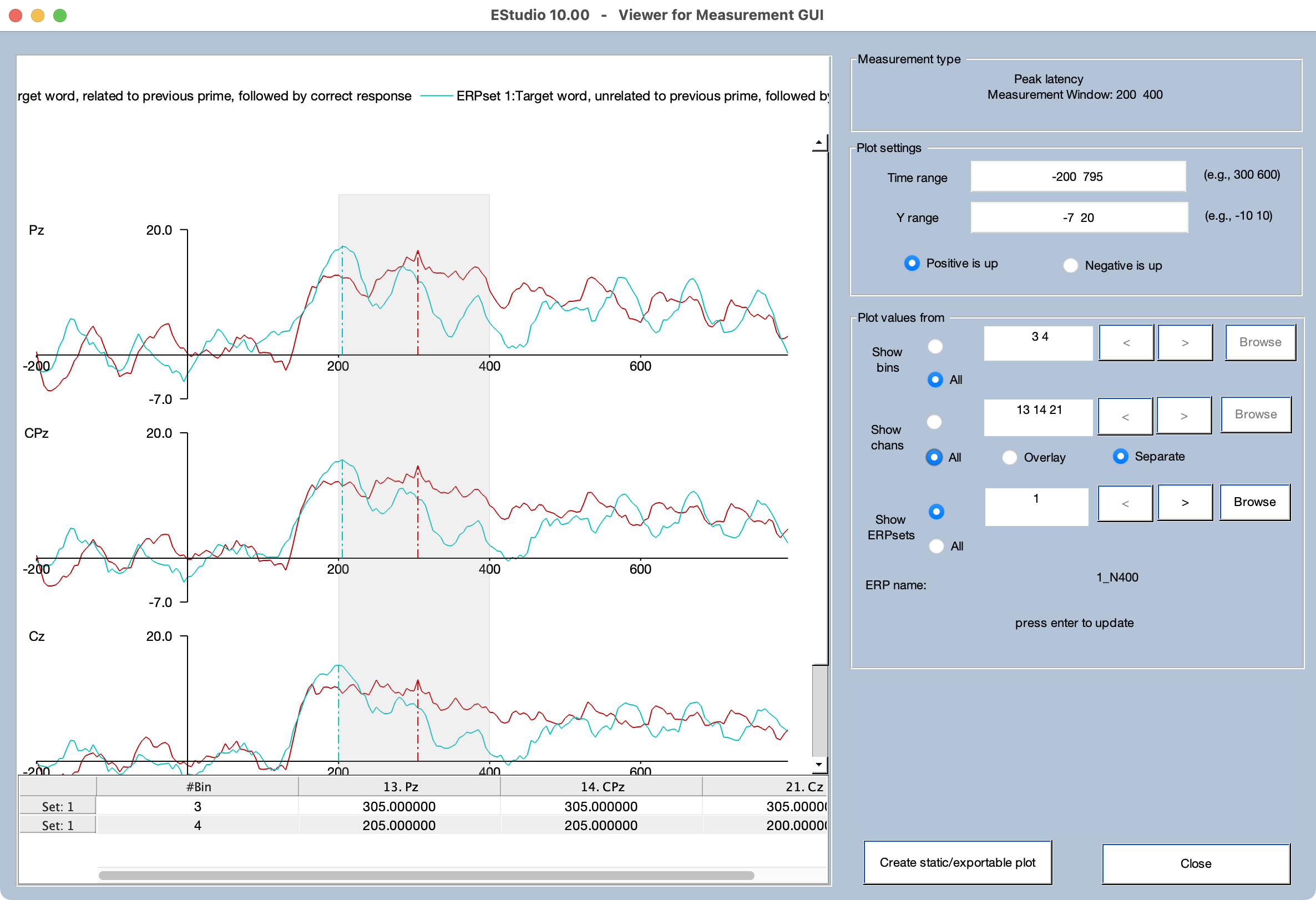
To create this plot shown in this screenshot, the settings on the right side of the window were set up to show All channels with a Separate plot region for each channel. In addition, All bins are selected. It is then possible to select which ERPset is shown by clicking the < and > buttons.
Note that the main ERPLAB Studio GUI is deactivated while the Preview window is open.
The gray region shows the specified measurement window (200–400 ms), and the red vertical line shows the time at which the peak latency was found (because peak latency was used for this example). The table at the bottom of the window shows the measured peak latency value for the currently displayed ERPsets, bins, and channels.
After you are done previewing the data, click Close in the Preview window to go back to the main Measurement Tool panel. You can then click Save measures to save the measured values to the specified text file. You can use the Options button to choose between two different file formats:
- One ERPset per line (wide format). This format is appropriate for many ANOVA-oriented statistical packages, such as JASP. In this format, all the measurements for a single ERPset (e.g., N bins x M channels) will be placed on a single line. That is, each line will contain the data from one participant (assuming that each ERPset represents one participant's data) and each column will be the measurement for a bin/channel combination. In many experiments, the number of columns is very large, making it not very human-friendly.
- One measurement per line (long format). This format is appropriate for other statistical packages, such as R, and for importing into Excel for use with pivot tables. In this format, a single measurement is provided on each line (e.g., a single combination of file, bin, and channel). Each line also contains information about which file, bin, and channel was measured on that line.
Each type of measurement requires that you specify a time window (or single time point) for measurement. For example, you might measure the peak or mean amplitude between 100 and 200 ms. However, depending on your sampling rate, you might not have sample points at exactly these times. ERPLAB therefore picks the closest sample points (except for the mean/integral/area measures), as described fully on the Timing Details page.
To increase precision, ERPLAB can resample the data at a higher sampling rate prior to measuring an amplitude or latency value. This is primarily valuable for the advanced latency measurement routines (e.g., when you are finding the latency at which the voltage has reached 50% of the peak voltage). You can control this by specifying the Interpolation Factor in the Options button for the measurement Type. If you use a factor of 1, no interpolation will be applied. If you use a value of greater than 1, the sampling rate will be increased by this factor (using spline interpolation). For example, if your original sampling rate was 512 Hz, and you specify an interpolation factor of 2, the data will be resampled at 1024 Hz. Details can be found on the Timing Details page.
Here are the different types of values that can be measured:
Instantaneous amplitude
This simply measures the amplitude at one latency (a single latency is specified in the Window text box).
Peak amplitude or latency
This finds the most positive or most negative amplitude within a specified time range (the starting and ending latencies of the time range are specified in the latency text box). The amplitude and/or latency of this peak is provided in the output file. If the number of points for local peak is nonzero in the Options, a peak is defined as the most positive or most negative value that is also (a) larger than the voltages in the one sample on either side of the peak, and (b) larger than the average of the N sample points on left side of the peak, and (c) larger than the average of the N sample points on the right side of the peak (where N is the value you specify in the Options window). If there is no point that meets this definition, then a warning message is printed in the Matlab command window and the simple peak (the most positive or negative point) or NaN is printed (depending on what is specified in the Options window). Note that this requires that the N sample points actually exist. If, for example, you ask for the local peak amplitude between 300 and 900 ms, with N set at 10, then the epoch length must be at least 10 sample points longer than 900 ms. Note: We strongly recommend that you use the local peak option; if you do, the Method section of your journal articles should indicate that you measured "local peak amplitude" or "local peak latency" (and not just "peak amplitude" and "peak amplitude").
Mean amplitude
This computes mean voltage within a specified time range (the starting and ending latencies of the time range are specified in the Window text box).
Integral and area amplitude
ERPLAB provides several options for computing what is often called "area amplitude," and to understand them you must first understand some terminology. Technically, the term "area" refers to the geometric shapes created by the boundary of the waveform and the zero line. Area can never be negative. When you want to allow the regions below the zero line to be considered negative, such that positive and negative regions will cancel each other, you will be measuring the "integral" of the waveform (over some time range).
When ERPLAB measures areas and integrals, it does so by treating each sample point as a rectangle that is one sample period wide and computing the area or integral numerically (as opposed to computing the values analytically by fitting a continuous function to the data). Some details are described on the Timing Details page.
The integral or area is measured between two fixed time points that you specify. You have 4 options for exactly what will be measured:
- Rectified area (negative values become positive)- This is the true area of the geometric regions formed by the combination of the baseline and the waveform. It is equivalent to taking the absolute value at each data point (i.e., rectifying the waveform) and then measuring the area. The resulting value is >= zero.
- Numeric integration (area for negatives subtracted from area for positives)- This is the integral of the waveform, which is equal to computing the sum of the voltages at each sample point in the measurement window and then scaling this sum to take the sampling rate into account. The resulting value can be either positive or negative. Note that the integral is equivalent to the mean amplitude, except that the mean is divided by the length of the measurement interval.
- Area for positive regions (negatives are zeroed)- This finds the area of the portions of the waveform that are above the zero line. This is equivalent to setting all negative values to zero and computing the area. The resulting value is >= zero.
- Area for negative regions (positives are zeroed)- This finds the area of the portions of the waveform that are below the zero line. This is equivalent to setting all positive values to zero, and computing the rectified area. The resulting value is >= zero.
Because area has a height (µV) and a width (seconds), the values from this routine are in units of µVs (microvolt seconds). That is, a 1 µV value over a 1 second period would have an area of 1.0 µVs, and a 1 µV value over a 100-ms period would have an area of 0.1 µVs.
Fractional area latency
This routine provides a measure of latency by finding the point that dividing the area under the curve into a specific fraction (specified by clicking the Options button). For example, if you want to find the midpoint of a component, you could do this by finding the point that divides the area under the curve into two equal regions (see screenshot below). This would be the "50% area latency" measure, and it works extremely well on large components like the P3 wave or on components that have been isolated by means of difference waves (see, e.g., Kiesel et al., 2008, Psychophysiology; Luck & Hillyard, 1990, Perception & Psychophysics; Luck, 1998, Psychological Science).
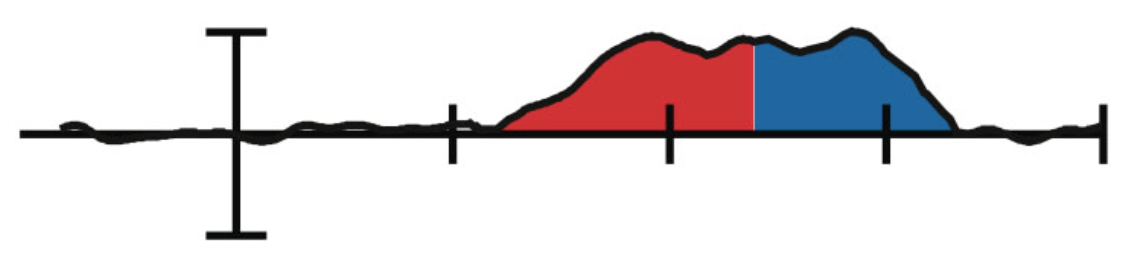
The same approach can be used to assess the onset or offset of a waveform. To estimate the onset, you could find something like the 15% area latency (the point at which 15% of the area is to the left of the point and 85% of the area is to the right). To estimate the offset, you could find something like the 85% area latency. The same four options that are available for using area/integral to measure amplitude are available for measuring fractional area amplitude.
Fractional peak latency
This routine provides a measure of onset latency by finding the peak amplitude and working backward in the waveform until the amplitude reaches a specified fraction of the peak amplitude (specified by clicking the Options button). For example, the figure below shows how the 50% peak latency is computed by finding the peak amplitude and then working backward until the voltage reaches 50% of this peak voltage. As in other peak measures, you can have it find a local peak amplitude rather than the absolute peak, and work backward to the point that is the requested fraction of the local peak amplitude. In many cases, this is the optimal method for computing onset latency (see, e.g., Kiesel et al., 2008, Psychophysiology; Luck et al., 2009, Psychophysiology).
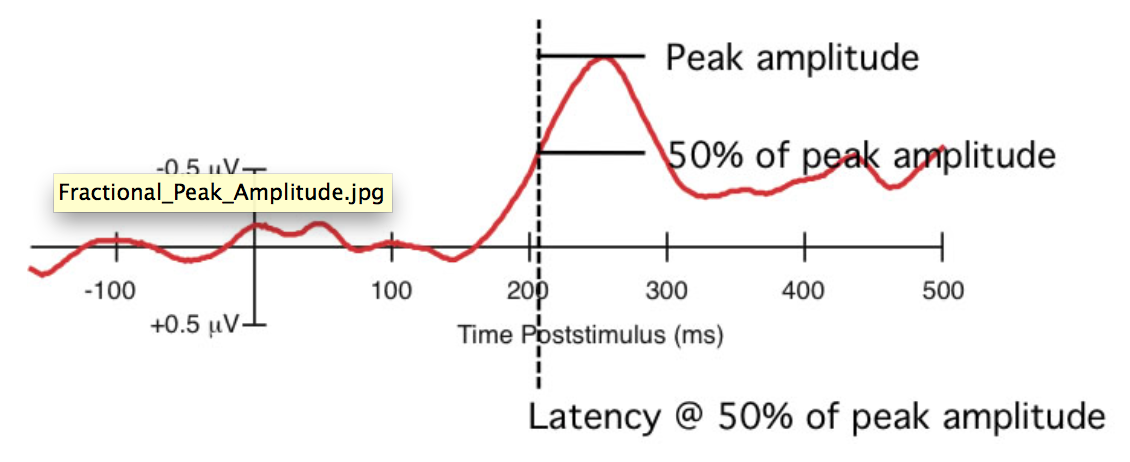
The above image shows the selection of a 50% peak 'onset'. That means that the value returned is the time before the peak at which the ERP is 50% as large as the peak. We also include an option to find the 'offset' - the first time after the peak that the ERP drops to 50% as large as the peak.