T1W2 Functions, Conditionals & Fruitful Functions - tstorrnetnz/teaching2025 GitHub Wiki

This week and next we continue revising our knowledge of Python by taking a look at functions and conditionals such as if and else.

You should remember that functions execute a block of code, for example:

def draw_a_circle()

Chapter 4 has a series of exercises to help you revise functions. Conditionals - if and else's should also be very familiar to you.

Chapter 5 has a series of exercises to help you revise these essential parts of programming.

Chapter 6 continues the work on functions by including return values and unit testing.

1. Write a void (non-fruitful) function to draw a square. Use it in a program to draw the image shown below. Assume each side is 20 units. (Hint: notice that the turtle has already moved away from the ending point of the last square when the program ends.) 

Five Squares

2. Write a program to draw this. Assume the innermost square is 20 units per side, and each successive square is 20 units bigger, per side, than the one inside it.

Nested Squares

3. Write a void function draw_poly(t, n, sz) which makes a turtle draw a regular polygon. When called with draw_poly(tess, 8, 50), it will draw a shape like this:

Regular polygon

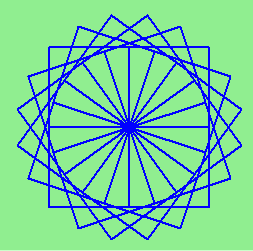
4. Draw this pretty pattern.

Regular Polygon

5. The two spirals in this picture differ only by the turn angle. Draw both.

Spirals

6. Write a void function draw_equitriangle(t, sz) which calls draw_poly from the previous question to have its turtle draw a equilateral triangle.

7. Write a fruitful function sum_to(n) that returns the sum of all integer numbers up to and including n. So sum_to(10) would be 1+2+3…+10 which would return the value 55.

8. Write a function area_of_circle(r) which returns the area of a circle of radius r.

9. Write a void function to draw a star, where the length of each side is 100 units. (Hint: You should turn the turtle by 144 degrees at each point.)

Star

10. Extend your program above. Draw five stars, but between each, pick up the pen, move forward by 350 units, turn right by 144, put the pen down, and draw the next star. You’ll get something like this:

Five Stars

What would it look like if you didn’t pick up the pen?

Conditionals - if and else's should also be very familiar to you.

1. Assume the days of the week are numbered 0,1,2,3,4,5,6 from Sunday to Saturday. Write a function which is given the day number, and it returns the day name (a string).

2. You go on a wonderful holiday (perhaps to jail, if you don’t like happy exercises) leaving on day number 3 (a Wednesday). You return home after 137 sleeps. Write a general version of the program which asks for the starting day number, and the length of your stay, and it will tell you the name of day of the week you will return on.

3. Give the logical opposites of these conditions

   a > b
   a >= b
   a >= 18  and  day == 3
   a >= 18  and  day != 3

4. What do these expressions evaluate to?

   3 == 3
   3 != 3
   3 >= 4
   not (3 < 4)

5. Complete this truth table:

   p	q	r	(not (p and q)) or r
   F	F	F	?
   F	F	T	?
   F	T	F	?
   F	T	T	?
   T	F	F	?
   T	F	T	?
   T	T	F	?
   T	T	T	?

6. Write a function which is given an exam mark, and it returns a string — the grade for that mark — according to this scheme:

   Mark	Grade
   >= 75	First
   [70-75)	Upper Second
   [60-70)	Second
   [50-60)	Third
   [45-50)	F1 Supp
   [40-45)	F2
   < 40	F3

   The square and round brackets denote closed and open intervals. A closed interval includes the number, and open interval excludes it. So 39.99999 gets grade F3, but 40 gets grade F2. Assume

   xs = [83, 75, 74.9, 70, 69.9, 65, 60, 59.9, 55, 50,
                       49.9, 45, 44.9, 40, 39.9, 2, 0]

   Test your function by printing the mark and the grade for all the elements in this list.

7. Modify the turtle bar chart program so that the pen is up for the small gaps between each bar.

8. Modify the turtle bar chart program so that the bar for any value of 200 or more is filled with red, values between [100 and 200) are filled with yellow, and bars representing values less than 100 are filled with green.

9. In the turtle bar chart program, what do you expect to happen if one or more of the data values in the list is negative? Try it out. Change the program so that when it prints the text value for the negative bars, it puts the text below the bottom of the bar.

10. Write a function find_hypot which, given the length of two sides of a right-angled triangle, returns the length of the hypotenuse. (Hint: x ** 0.5 will return the square root.)

11. Write a function is_rightangled which, given the length of three sides of a triangle, will determine whether the triangle is right-angled. Assume that the third argument to the function is always the longest side. It will return True if the triangle is right-angled, or False otherwise.

    Hint: Floating point arithmetic is not always exactly accurate, so it is not safe to test floating point numbers for equality. If a good programmer wants to know whether x is equal or close enough to y, they would probably code it up as:

    if  abs(x-y) < 0.000001:    # If x is approximately equal to y
        ...

12. Extend the above program so that the sides can be given to the function in any order.

13. If you’re intrigued by why floating point arithmetic is sometimes inaccurate, on a piece of paper, divide 10 by 3 and write down the decimal result. You’ll find it does not terminate, so you’ll need an infinitely long sheet of paper. The representation of numbers in computer memory or on your calculator has similar problems: memory is finite, and some digits may have to be discarded. So small inaccuracies creep in. Try this script:

    import math
    a = math.sqrt(2.0)
    print(a, a*a)
    print(a*a == 2.0)

All of the exercises below should be added to a single file. In that file, you should also add the test and test_suite scaffolding functions shown above, and then, as you work through the exercises, add the new tests to your test suite. (If you open the online version of the textbook, you can easily copy and paste the tests and the fragments of code into your Python editor.)

After completing each exercise, confirm that all the tests pass.

1. The four compass points can be abbreviated by single-letter strings as “N”, “E”, “S”, and “W”. Write a function turn_clockwise that takes one of these four compass points as its parameter, and returns the next compass point in the clockwise direction. Here are some tests that should pass:

    test(turn_clockwise("N") == "E")
    test(turn_clockwise("W") == "N")
   
    You might ask “What if the argument to the function is some other value?” For all other cases, the function should return the value `None`:
   
    test(turn_clockwise(42) == None)
    test(turn_clockwise("rubbish") == None)
   

2. Write a function day_name that converts an integer number 0 to 6 into the name of a day. Assume day 0 is “Sunday”. Once again, return None if the arguments to the function are not valid. Here are some tests that should pass:

    test(day_name(3) == "Wednesday")
    test(day_name(6) == "Saturday")
    test(day_name(42) == None)
   

3. Write the inverse function day_num which is given a day name, and returns its number:

    test(day_num("Friday") == 5)
    test(day_num("Sunday") == 0)
    test(day_num(day_name(3)) == 3)
    test(day_name(day_num("Thursday")) == "Thursday")
   

   Once again, if this function is given an invalid argument, it should return None:

    test(day_num("Halloween") == None)
   

4. Write a function that helps answer questions like ‘“Today is Wednesday. I leave on holiday in 19 days time. What day will that be?”’ So the function must take a day name and a delta argument — the number of days to add — and should return the resulting day name:

        test(day_add("Monday", 4) ==  "Friday")
        test(day_add("Tuesday", 0) == "Tuesday")
        test(day_add("Tuesday", 14) == "Tuesday")
        test(day_add("Sunday", 100) == "Tuesday")
   

   Hint: use the first two functions written above to help you write this one.

5. Can your day_add function already work with negative deltas? For example, -1 would be yesterday, or -7 would be a week ago:

    test(day_add("Sunday", -1) == "Saturday")
    test(day_add("Sunday", -7) == "Sunday")
    test(day_add("Tuesday", -100) == "Sunday")
   

   If your function already works, explain why. If it does not work, make it work.

   Hint: Play with some cases of using the modulus function % (introduced at the beginning of the previous chapter). Specifically, explore what happens to x % 7 when x is negative.

6. Write a function days_in_month which takes the name of a month, and returns the number of days in the month. Ignore leap years:

    test(days_in_month("February") == 28)
    test(days_in_month("December") == 31)
   

   If the function is given invalid arguments, it should return None.

7. Write a function to_secs that converts hours, minutes and seconds to a total number of seconds. Here are some tests that should pass:

    test(to_secs(2, 30, 10) == 9010)
    test(to_secs(2, 0, 0) == 7200)
    test(to_secs(0, 2, 0) == 120)
    test(to_secs(0, 0, 42) == 42)
    test(to_secs(0, -10, 10) == -590)
   

8. Extend to_secs so that it can cope with real values as inputs. It should always return an integer number of seconds (truncated towards zero):

    test(to_secs(2.5, 0, 10.71) == 9010)
    test(to_secs(2.433,0,0) == 8758)
   

9. Write three functions that are the “inverses” of to_secs:

    `hours_in` returns the whole integer number of hours represented by a total number of seconds.
   
    `minutes_in` returns the whole integer number of left over minutes in a total number of seconds, once the hours have been taken out.
   
    `seconds_in` returns the left over seconds represented by a total number of seconds.
   

   You may assume that the total number of seconds passed to these functions is an integer. Here are some test cases:

    test(hours_in(9010) == 2)
    test(minutes_in(9010) == 30)
    test(seconds_in(9010) == 10)
   

It won’t always be obvious what is wanted …

In the third case above, the requirement seems quite ambiguous and fuzzy. But the test clarifies what we actually need to do.

Unit tests often have this secondary benefit of clarifying the specifications. If you write your own test suites, consider it part of the problem-solving process as you ask questions about what you really expect to happen, and whether you’ve considered all the possible cases.

Given our emphasis on thinking like a computer scientist, you might enjoy reading at least one reference about thinking, and about fun ideas like fluid intelligence, a key ingredient in problem solving. See, for example, http://psychology.about.com/od/cognitivepsychology/a/fluid-crystal.htm. Learning Computer Science requires a good mix of both fluid and crystallized kinds of intelligence.

10. Which of these tests fail? Explain why.

    test(3 % 4 == 0)
    test(3 % 4 == 3)
    test(3 / 4 == 0)
    test(3 // 4 == 0)
    test(3+4  *  2 == 14)
    test(4-2+2 == 0)
    test(len("hello, world!") == 13)
    

11. Write a compare function that returns 1 if a > b, 0 if a == b, and -1 if a < b

    test(compare(5, 4) == 1)
    test(compare(7, 7) == 0)
    test(compare(2, 3) == -1)
    test(compare(42, 1) == 1)
    

12. Write a function called hypotenuse that returns the length of the hypotenuse of a right triangle given the lengths of the two legs as parameters:

    test(hypotenuse(3, 4) == 5.0)
    test(hypotenuse(12, 5) == 13.0)
    test(hypotenuse(24, 7) == 25.0)
    test(hypotenuse(9, 12) == 15.0)
    

13. Write a function slope(x1, y1, x2, y2) that returns the slope of the line through the points (x1, y1) and (x2, y2). Be sure your implementation of slope can pass the following tests:

    test(slope(5, 3, 4, 2) == 1.0)
    test(slope(1, 2, 3, 2) == 0.0)
    test(slope(1, 2, 3, 3) == 0.5)
    test(slope(2, 4, 1, 2) == 2.0)
    

Then use a call to slope in a new function named intercept(x1, y1, x2, y2) that returns the y-intercept of the line through the points (x1, y1) and (x2, y2)

    test(intercept(1, 6, 3, 12) == 3.0)
    test(intercept(6, 1, 1, 6) == 7.0)
    test(intercept(4, 6, 12, 8) == 5.0)

14. Write a function called is_even(n) that takes an integer as an argument and returns True if the argument is an even number and False if it is odd.

    Add your own tests to the test suite.

15. Now write the function is_odd(n) that returns True when n is odd and False otherwise. Include unit tests for this function too.

    Finally, modify it so that it uses a call to is_even to determine if its argument is an odd integer, and ensure that its test still pass.

16. Write a function is_factor(f, n) that passes these tests:

    test(is_factor(3, 12))
    test(not is_factor(5, 12))
    test(is_factor(7, 14))
    test(not is_factor(7, 15))
    test(is_factor(1, 15))
    test(is_factor(15, 15))
    test(not is_factor(25, 15))
    

    An important role of unit tests is that they can also act as unambiguous “specifications” of what is expected. These test cases answer the question “Do we treat 1 and 15 as factors of 15”?

17 Write is_multiple to satisfy these unit tests:

    test(is_multiple(12, 3))
    test(is_multiple(12, 4))
    test(not is_multiple(12, 5))
    test(is_multiple(12, 6))
    test(not is_multiple(12, 7))

Can you find a way to use `is_factor` in your definition of `is_multiple`?

18. Write the function f2c(t) designed to return the integer value of the nearest degree Celsius for given temperature in Fahrenheit. (hint: you may want to make use of the built-in function, round. Try printing round.__doc__ in a Python shell or looking up help for the round function, and experimenting with it until you are comfortable with how it works.)

    test(f2c(212) == 100)     # Boiling point of water
    test(f2c(32) == 0)        # Freezing point of water
    test(f2c(-40) == -40)     # Wow, what an interesting case!
    test(f2c(36) == 2)
    test(f2c(37) == 3)
    test(f2c(38) == 3)
    test(f2c(39) == 4)
    

19. Now do the opposite: write the function c2f which converts Celsius to Fahrenheit:

    test(c2f(0) == 32)
    test(c2f(100) == 212)
    test(c2f(-40) == -40)
    test(c2f(12) == 54)
    test(c2f(18) == 64)
    test(c2f(-48) == -54)