External - tstorrnetnz/teaching2022 GitHub Wiki
The external (quick reminder 3 credits), is a DCAT (digital test at school and held in 2 months time.). My experience is that students can do this very successfully. The topic we are doing is Formal Languages. The external that you do about your project is very straightforward - I will cover this in just one lesson before the end of term.
Mt Hutt College Weds 26 Oct T4W2
Fiordland College Weds 26 Oct T4W2
Marian College Thursday 27 Oct T4 W2
St Bede's Thursday 27 Oct T4 W2
Christchurch Adventist School Thursday 20 Oct T4W1
Dunstan High School Weds 26 Oct T4W2
There are 3 areas to this and 2 main resources.
The 3 Areas:
Finite State Automata Resource chapters 15.1, 15.2 and 15.3 of the Computer Science Field Guide.
Regular Expressions Resource chapter 15.4 of the Computer Science Field Guide
Context Free Grammars Resource chapter 15.5 of the Computer Science Field Guide
We will work through each of the areas separately.
You will need to read/do all the activities in each of the sections above, as well as the activities in class.

Short video series (watch in your own time about 15 minutes total)
We will/you need to work through the exercises in chapters 15.1, 15.2 and 15.3 of the Computer Science Field Guide.
Exorcisor is available on the internet archive https://web.archive.org/web/20161206072501/http://www.swisseduc.ch/compscience/exorciser/download.html
After doing these exercises, you should be able able to understand how FSA’s work and what they are used to represent including: Accepting state Transitions Valid string Advantages/disadvantages of FSA’s
- Alphabet: The list of all possible inputs (e.g. a, b etc)
- Transitions: The connections between the different states
- Accepting state: The state when a FSA can stop/finish/complete. There must be at least one accepting state.
- Empty String: no input. If the accepting state is also the start of the FSA, then an empty string will result in an accepting state.
- Trap state: A state that you cannot get out of!
 Here is the required reading and exercises
Here is the required reading and exercises
https://www.csfieldguide.org.nz/en/chapters/formal-languages/regular-expressions/
Key points:
- Regular expressions are used for matching Strings (text/numbers) and are very powerful.
- Most programming languages have the ability to use regular expressions
- Regular expressions and Finite state automata are interchangeable - every FSA can be made into a RE (and vice versa)
- You need to be able to make and read simple regular expressions
- The challenges at Designing Regular Expressions in the above link are good challenges to test yourself (see below)
Here are some ideas for regular expressions for you to try to create. You can check them using the Regular Expression Searcher as we did earlier, but you'll need to make up your own text to check your regular expression. When testing your expressions, make sure that they not only accept correct strings, but reject ones that don't match, even if there's just one character missing. You may find it easier to have one test match string per line in the test area. You can force your regular expression to match a whole line by putting "^" (start of line) before the regular expression, and "$" (end of line) after it. For example, "^a+$" only matches lines that have nothing but "a"s on them. Here are some challenges to try to create regular expressions for:
- local forms of non-personalised number plates (e.g. AB1234 or ABC123 in New Zealand)
- any extended form of the word "hello", e.g. "helloooooooooooo"
- variants of "aaaarrrrrgggggghhhh"
- a 24-hour clock time (e.g. 23:00) or a 12-hour time (e.g. 11:55 pm)
- a bank account or credit card number
- a credit card expiry date (must have 4 digits e.g 01/15)
- a password that must contain at least 2 digits (don't test it against your own!)
- a date
- a phone number (choose your format e.g. mobile only, national numbers, or international)
- a dollar amount typed into a banking website, which should accept various formats like "1.43", "1", "21.43", and ",000", but not "21$", "21.5", "5,0000.00", and "300$".
- acceptable identifiers in your programming language (usually something like a letter followed by a combination of letters, digits and some punctuation symbols)
- an integer in your programming language (allow for + and - at the front, and some languages allow suffixes like L, or prefixes like 0x)
- an IP address (e.g. 172.16.5.2 or 172.168.10.10:8080)
- a MAC address for a device (e.g. e1:ce:8f:2a:0a:ba)
- postal codes for several countries e.g. NZ: 8041, Canada: T2N 1N4, US: 90210
- a (limited) http URL, such as "http://abc.xyz", "http://abc.xyz#conclusion", "http://abc.xyz?search=fgh".
 The third and final ‘new’ thing for the external is something called Context Free Grammars. The main resource for CFG’s is this Chapter in the CS Field Guide.
The third and final ‘new’ thing for the external is something called Context Free Grammars. The main resource for CFG’s is this Chapter in the CS Field Guide.
The notes below are just a quick summary of the web pages above - please work through it!
You will need to watch this video that demonstrates the ‘test’ system we will use.
Key terms:
- Each rule is called a production.
- Symbols on the left hand side of a rule (that can be replaced when the production runs) are called non-terminals
- Symbols on the right hand side of a rule that do not occur on the left hand side of other rules (so cannot be replaced when the production runs) are called terminals
Some simple challenges
- Here is the live interactive that you can use to show that you understand CFG’s
- And another slight different grammar for you to try out
- Here is one that is slightly more challenging
- Syntax errors are when you have typed something in a programming language that breaks a rule/production of the Context Free Grammar for that programming language.
CFG’s can also be used to make mathematical expressions Video - explaining this is here
Try this equation builder out here.
Here are a range of grammars and challenges for you to try. None of them do anything that a CFG is likely to be used for in practice, but they will give you a feel for how CFGs work. Remember that you can type your own test strings into the box as examples - it’s worth including some that can’t be parsed, to see how the grammar works when it finds a syntax error.
- This grammar generates a pattern of “a” and “b” mixed together, then a “c”, then the original pattern backwards. It can be strangely satisfying to solve, and it’s something you can’t check with a regular language (i.e. a regular expression or FSA).
- Here’s a similar grammar, but it generates some number of “a”s, followed by twice as many “b”s.
- This grammar generates strings that have a number of “a”s, followed by a number of “b”s, then a number of”‘c”s that is the sum of the number of “a”s and “b”s.
- This grammar generates strings of balanced brackets. Normally there would be other symbols involved, but we’re just worrying if every opening bracket has a matching closed bracket. It can get a bit hard to follow, but it’s all very logical!
- Here is a version of the grammar for an expression that will work if you paste the examples into a spreadsheet. The only difference from the one above is that it puts an “‘=”’ sign at the front of the expression.
- This grammar generates binary numbers that are multiples of three. The examples include some numbers that aren’t multiples of 3, since you can’t be sure it’s working unless it rejects incorrect strings as well as accepting correct ones. (As it happens, this language can also be generated using a regular expression.)
- This grammar has a language that could have been implemented using a regular language - you can probably work out the FSA that would accept correct strings.
- This is a silly grammar based on the English language. English can’t usually be represented as a formal language, but this exercise gives you an idea of how the terminology in formal languages relates to ideas in English grammar.
- Read through the whole paper first - the questions are not long so this will not take too much time.
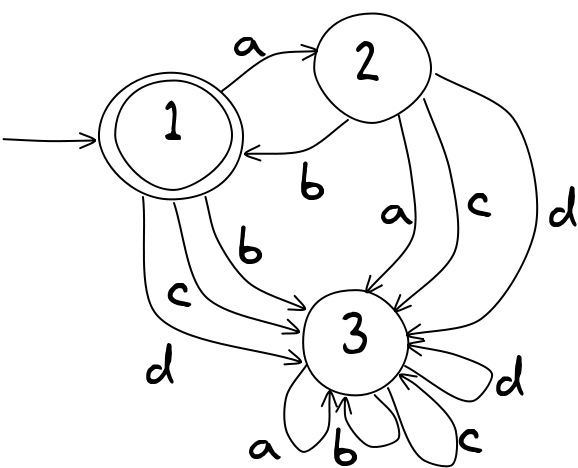
So far we have had a look at simple Finite State Automata (sometimes also called Finite state Machines, FSM's). Here are a few more things that would be useful for higher grades:
FSA's can be divided into two categories Deterministic and non-Deterministic FSA's. The difference is quite simple. The FSA's we have looked at so far are deterministic. Each input can have only one transition. This means that we know (can determine) what the next state is. Non-deterministic FSA's have more than one transition for each input. This means you cannot know what the next state is.
Formal Definition of a Deterministic FSA
A DFA can be represented by a 5-tuple (Q, ∑, δ, q0, F) where −
* Q is a finite set of states.
-
∑ is a finite set of symbols called the alphabet. -
δ is the transition function where δ: Q × ∑ → Q -
q0 is the initial state from where any input is processed (q0 ∈ Q). -
F is a set of final state/states of Q (F ⊆ Q).
Transition function δ as shown by the following table −
| Present State | Next State for Input 0 | Next State for Input 1 |
|---|---|---|
| a | a | b |
| b | c | a |
| c | b | c |
For a non-deterministic FSA
Formal Definition of an NDFA
An NDFA can be represented by a 5-tuple (Q, ∑, δ, q0, F) where −
Q is a finite set of states.
∑ is a finite set of symbols called the alphabets.
δ is the transition function where δ: Q × ∑ → 2Q
(Here the power set of Q (2Q) has been taken because in case of NDFA, from a state, transition can occur to any combination of Q states)
q0 is the initial state from where any input is processed (q0 ∈ Q).
F is a set of final state/states of Q (F ⊆ Q).
Let a non-deterministic finite automaton be →
- Q = {a, b, c}
- ∑ = {0, 1}
- q0 = {a}
- F = {c}
The transition function δ as shown below −
| Present State | Next State for Input 0 | Next State for Input 1 |
|---|---|---|
| a | a, b | b |
| b | c | a, c |
| c | b, c | c |
The following table lists the differences between DFA and NDFA.
| DFA | NDFA |
|---|---|
| The transition from a state is to a single particular next state for each input symbol. Hence it is called deterministic. | The transition from a state can be to multiple next states for each input symbol. Hence it is called non-deterministic. |
| Empty string transitions are not seen in DFA. | NDFA permits empty string transitions. |
| Backtracking is allowed in DFA | In NDFA, backtracking is not always possible. |
| A string is accepted by a DFA, if it transits to a final state. | A string is accepted by a NDFA, if at least one of all possible transitions ends in a final state. |
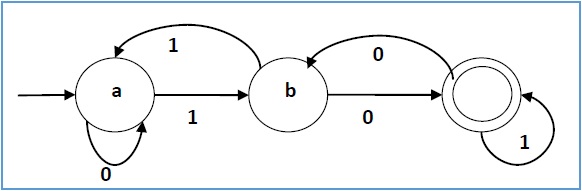
Trap states
Here's another FSA to consider:
It's fairly clear what it will accept: strings like "ab", "abab", "abababababab", and, of course ϵ
. But there are some missing transitions: if you are in state 1 and get a "b" there's nowhere to go. If an input cannot be accepted, it will be rejected, as in this case. We could have put in a trap state to make this clear:
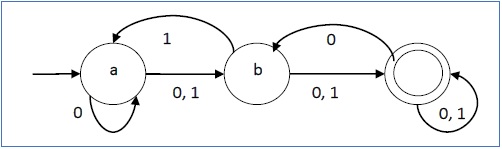
But things can get out of hand. What if there are more letters in the alphabet? We'd need something like this:
So, instead, we just say that any unspecified transition causes the input to be rejected (that is, it behaves as though it goes into a trap state). In other words, it's fine to use the simple version above, with just two transitions.
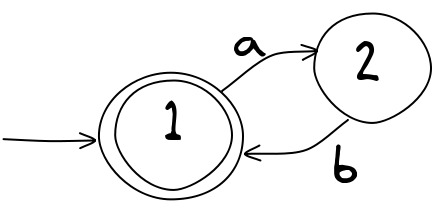
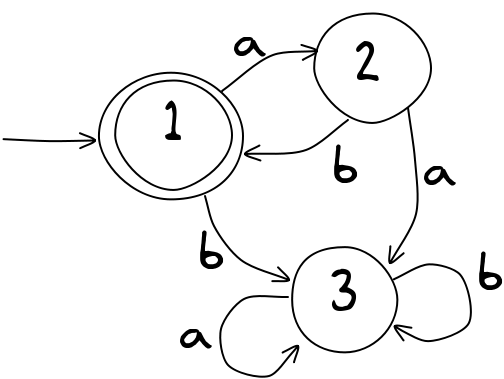
Multiple accepting states
FSA's can have multiple accepting states. There is a nice problem (and solution) here:
What is the correct FSA representation of this string?
that shows this well. Read through to the end to see the working out.
What are the similarities and differences and differences between Finite State Automata, Regular Expressions and Context Free Grammars?
Activity one On a piece of paper, draw a FSA that accepts your first name - spelled correctly with either a lower or uppercase first letter. Do the same but as a regular expression. This should be quite straightforward. In fact FSA’s and Regular expressions are just different ways of expressing the same ideas and are interchangeable (for Strings at least).
Regular expressions are used in a variety (almost all) programming languages - while it would be impossible to use a FSA while programming.
FSA’s are good for representing the flow of possibilities in a menu - for example on a TV remote or dishwasher, and also in designing digital circuits - but regular expressions are not so good at this.
Both FSA’s and Regular Expressions are examples of regular languages. These follow rules that allow only a fixed order of words/symbols.
Some interesting uses of the ideas in FSA’s include gene sequencing - (think covid 19), automated car number plate checking, - can you think of any others?
CFG’s are much more powerful than FSA’s/Regular Expressions. CFG’s have more flexibility than FSA’s/regular expressions and can make expressions that FSA’s cannot.
Activity Two
- Create a FSA that accepts abbb
- Create a FSA that accepts aabbbbbb
- Create a FSA that accepts aaaabbbbbbbbbbbb
- Can an FSA be created that accepts xa 3xb (ie for any number of A's accept the A's with 3 times the number of B's)?
- Can this be done with Context Free Grammars? -Try using this example
CFG’s are used to define programming languages.
CFG’s for example are used to see if a line of code fits the rules of a programming language (think about ending a line in Java with a ;) whereas a regular expression cannot do that.
For this assessment you need three images - to be provided to your school beforehand:
- An image of your development process (Kanban board or github commits summary)
- An image of some sample code
- An image of you programme GUI (or output if non-gui based)
The past papers give a good guide to what is expected in the assessment. Some tips are below:
You will have made decisions during your project that affect both the outcome (your final'thing'),and the development process itself (how you went about managing your project). You also will have made decisions about the tools and techniques used as you made your outcome.
The development process includes:
- Planning with your stakeholder to find their needs
- Programming sprints
- Meeting with your stakeholder to get feedback
- Testing
- Improvements
Tools include:
- Github
- Netbeans any other editor
- Any other programme
Techniques include:
- Using csv file storage or serialization or hashmaps
- Making objects and classes
- Error correction
- Using the GUI editor
The questions have previously asked:
- For a brief description of your outcome and what it's purpose/function is
- How decisions you have made (referring to tools and techniques) have affected/are linked/can be seen in the final outcome.
- How decisions you have made (referring to tools and techniques) have affected/are linked/can be seen in the development process.
- What changes you made to any of these decisions as you developed your outcome, and why
- The contribution of stakeholder feedback to the outcome and the process.
- What you have learned during the process.
- What you would do differently - for both the development process and the outcome, if given the chance.
- How your outcome addressed relevant implications/end user considerations.
These questions may ask you to:
- Describe
- Explain (with reasons - I did this because)
- Evaluate/Analyse (positives and negatives, include some judgements - ie better worse)
- Read through the whole paper first - the questions are not long so this will not take too much time.
- Refer to specific examples of your work.
- Imagine you are explaining this to your Y7/8 homeroom teacher (i.e. smart enough to understand but knows very little about the subject)
- Use: because, this means that, so that - this is an easy step up from A to M
Remember we are only looking at the Formal Languages questions
and for the project external