Skip List - tenji/ks GitHub Wiki

跳表

跳跃表（简称跳表）由美国计算机科学家 William Pugh 发明于 1989 年。他在论文《Skip lists: a probabilistic alternative to balanced trees》中详细介绍了跳表的数据结构和插入删除等操作。

跳表对标的是平衡树（AVL Tree）和二分查找，是一种 插入/删除/搜索 复杂度都是 O(log n) 的数据结构。原理是在原有的有序链表上面增加了多级索引，通过索引来实现快速查找。它最大的优势是原理简单、容易实现、方便扩展、效率更高。因此在一些热门的项目里用来替代平衡树，如 redis, leveldb 等。

一、基本概念

  • Level（级别）：SkipList 由多个级别组成。底层（0 级）是包含所有元素的常规链表。每个较高级别都充当“快速通道”，包含较少的元素并跳过较低级别中的多个元素。
  • Probability and height（概率和高度）：元素出现的级别数由概率决定，每个位于第 i 层的节点有 p 的概率出现在第 i + 1 层，p 为常数。
  • Head Pointers（头指针）：每个级别都有一个头指针，指向该级别的第一个元素，以便于快速访问每个级别的元素。

Probability（概率）一般建议取值是多少？

正常来讲，Probability 取值越小，跳表的级别/层数越低。Probability 一般取值是 1/2，但是这个不是强制的，比如 Redis 中的跳表 p = 1/4

一个元素级别/层数可以使用以下部分代码生成：

// 理论来讲，一级索引中元素个数应该占原始数据的 50%，二级索引中元素个数占 25%，三级索引12.5% ，一直到最顶层。
// 因为这里每一层的晋升概率是 50%。对于每一个新插入的节点，都需要调用 randomLevel 生成一个合理的层数。
// 该 randomLevel 方法会随机生成 1~MAX_LEVEL 之间的数，且 ：
//        50%的概率返回 1
//        25%的概率返回 2
//      12.5%的概率返回 3 ...
private int randomLevel() {
    int level = 1;

    while (Math.random() < SKIPLIST_P && level < MAX_LEVEL)
      level += 1;
    return level;
}

二、基本思想

首先，跳表处理的是有序的链表，如下：

这个链表中，搜索和插入一个数并保持链表有序，时间复杂度都是 O(n)。

那么如何提高搜索的速度呢？很简单，做个索引：

如上图，我们新创建一个链表，它包含的元素为前一个链表的偶数个元素。这样在搜索一个元素时，我们先在上层链表进行搜索，当元素未找到时再到下层链表中搜索。例如搜索数字 19 时的路径如下图：

先在上层中搜索，到达节点 17 时发现下一个节点为 21，已经大于 19，于是转到下一层搜索，找到的目标数字 19。 我们知道上层的节点数目为 n/2 ，因此，有了这层索引，我们搜索的时间复杂度降为了：O(n/2) 。同理，我们可以不断地增加层数，来减少搜索的时间：

在上面的 4 层链表中搜索 25，在最上层搜索时就可以直接跳过 21 之前的所有节点，因此十分高效。

更一般地，如果有 k 层，我们需要的搜索次数会小于 ⌈ $\frac{n}{2k}$ ⌉ + k，这样当层数 k 增加到 ⌈ $\log_2 n$ ⌉ 时，搜索的时间复杂度就变成了 $log n$。其实这背后的原理和二叉搜索树或二分查找很类似，通过索引来跳过大量的节点，从而提高搜索效率。

三、复杂度

  • 期望空间复杂度：O(n)
  • 期望时间复杂度都：O( $\log n$ )

四、复杂度证明

...

五、Java 实现

5.1 跳表类

public class SkipList {

  private Node head = new Node();  // 带头链表
  private static final float SKIPLIST_P = 0.5f;
  private static final int MAX_LEVEL = 16;
  private int levelCount = 1;

  ...
}

5.2 节点结构

class Node {
  private int data = -1;
  private Node forwards[] = new Node[MAX_LEVEL];
  private int maxLevel = 0;

  @Override
  public String toString() {
    StringBuilder builder = new StringBuilder();
    builder.append("{ data: ");
    builder.append(data);
    builder.append("; levels: ");
    builder.append(maxLevel);
    builder.append(" }");

    return builder.toString();
  }
}

一个结点有 maxLevel 个指针？

5.3 搜索

方法流程：

  1. 从最高层索引开始遍历；
  2. 当前元素大小不满足小于搜索 value 值时，下降到下一层索引继续遍历，直到原始链表；
  3. 查询到数据则返回对应结点。
public Node search(int value) {
  Node p = head;
  for (int i = levelCount - 1; i >= 0; --i) {
    while (p.forwards[i] != null && p.forwards[i].data < value) {
      p = p.forwards[i];
    }
  }

  if (p.forwards[0] != null && p.forwards[0].data == value) {
    return p.forwards[0];
  } else {
    return null;
  }
}

5.4 删除

方法流程：

  1. 遍历每一层索引，找到需要删除元素对应的位置；
  2. 遍历每一层索引，将对应的元素删除；
  3. 更新索引层数。
public void delete(int value) {
  Node[] update = new Node[levelCount];
  Node p = head;
  for (int i = levelCount - 1; i >= 0; --i) {
    while (p.forwards[i] != null && p.forwards[i].data < value) {
      p = p.forwards[i];
    }
    update[i] = p;
  }

  if (p.forwards[0] != null && p.forwards[0].data == value) {
    for (int i = levelCount - 1; i >= 0; --i) {
      if (update[i].forwards[i] != null && update[i].forwards[i].data == value) {
        update[i].forwards[i] = update[i].forwards[i].forwards[i];
      }
    }
  }

  while (levelCount>1&&head.forwards[levelCount]==null){
    levelCount--;
  }

}

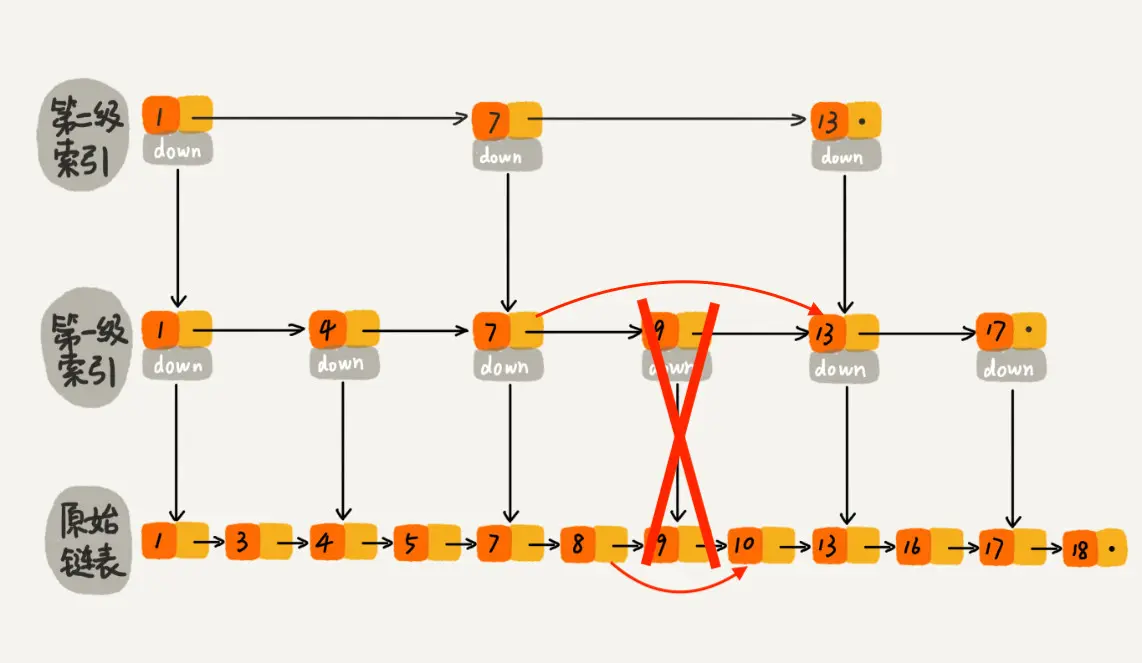
以下是从跳表中删除数据 9 的示意图：

跳表删除数据时，要把索引中对应节点也要删掉。如下图所示，如果要删除元素 9，需要把原始链表中的 9 和第一级索引的 9 都删除掉。

5.5 插入

方法流程：

  1. 通过 randomLevel() 函数确定该元素需要插入的索引级别，假设函数返回的 level 是 3，那么需要插入 0, 1, 2 级索引；
  2. 遍历每一层索引，找到新元素需要插入的位置（因为每一层索引的元素都是升序的，找到比插入值小的最后一个位置即可）；
  3. 遍历每一层索引，将新元素插入指定的位置；
  4. 更新索引层数。
public void insert(int value) {
  int level = randomLevel();
  Node newNode = new Node();
  newNode.data = value;
  newNode.maxLevel = level;
  Node update[] = new Node[level];
  for (int i = 0; i < level; ++i) {
    update[i] = head;
  }

  // record every level largest value which smaller than insert value in update[]
  Node p = head;
  for (int i = level - 1; i >= 0; --i) {
    while (p.forwards[i] != null && p.forwards[i].data < value) {
      p = p.forwards[i];
    }
    update[i] = p;// use update save node in search path
  }

  // in search path node next node become new node forwords(next)
  for (int i = 0; i < level; ++i) {
    newNode.forwards[i] = update[i].forwards[i];
    update[i].forwards[i] = newNode;
  }

  // update node hight
  if (levelCount < level) levelCount = level;
}

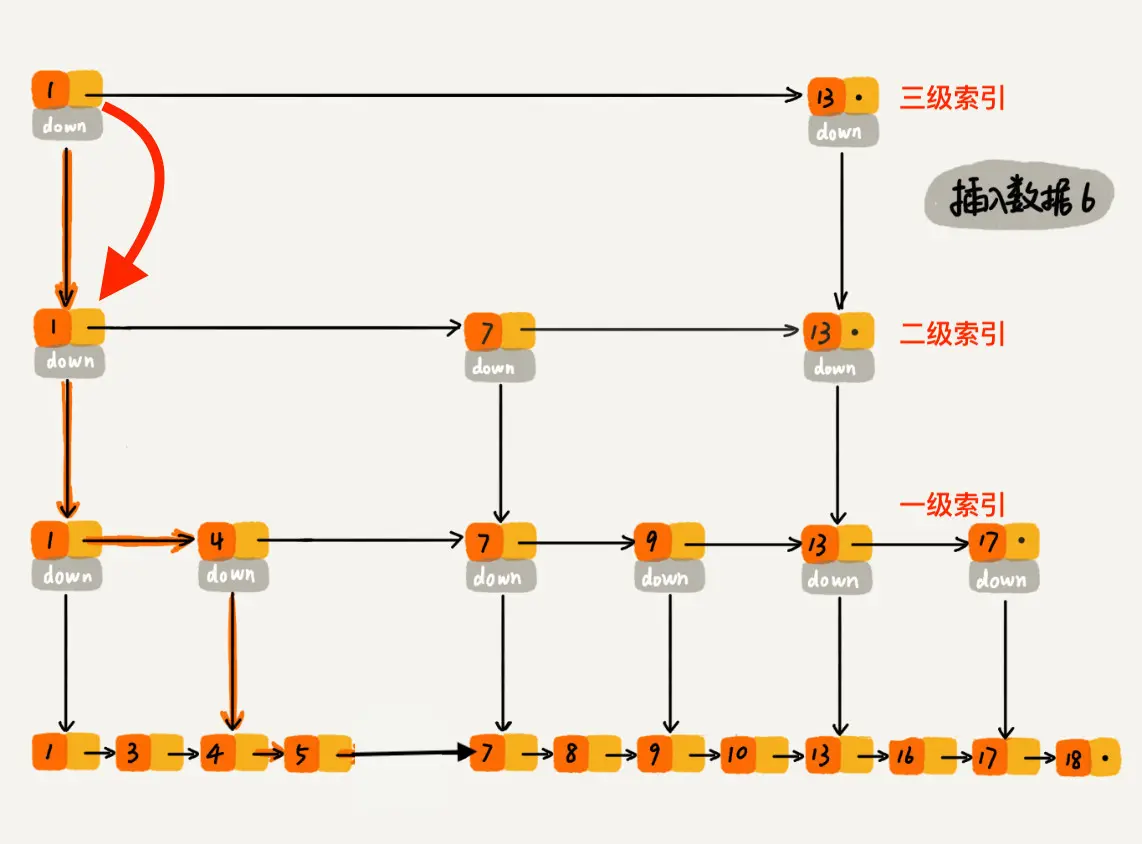
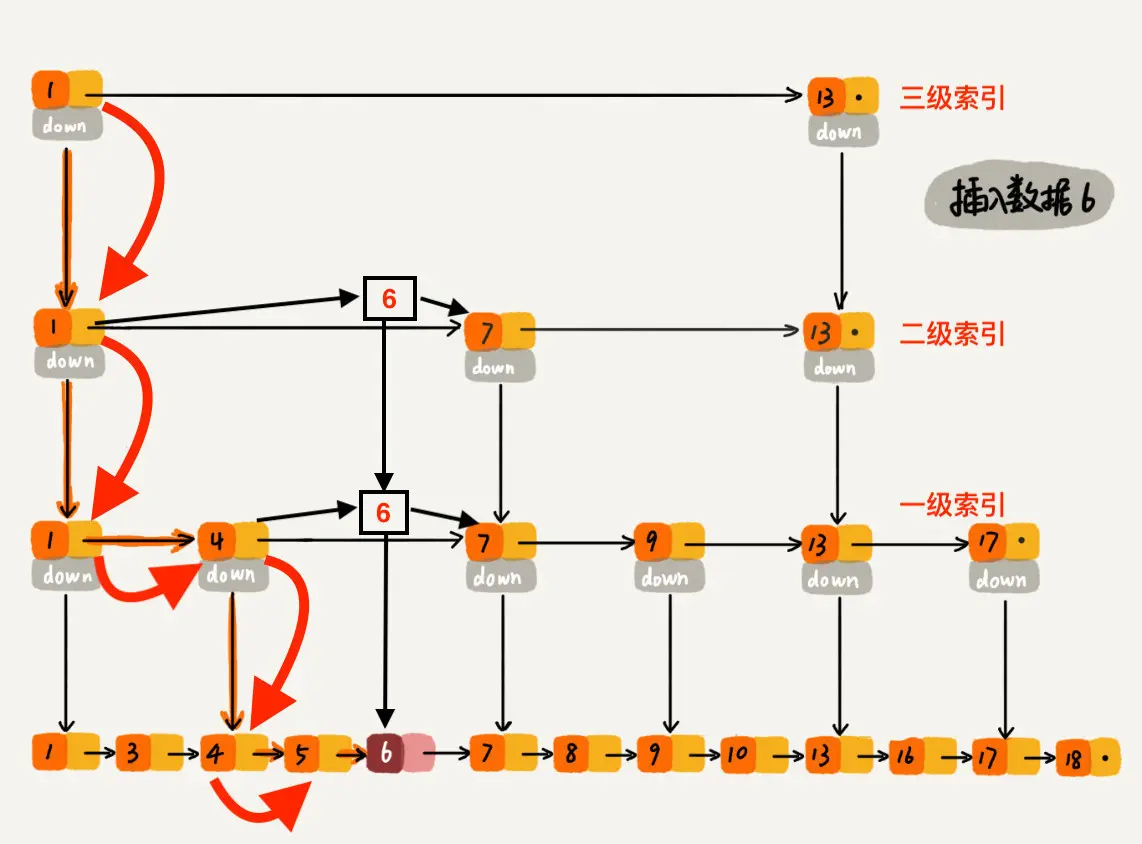
以下是将数据 6 插入到跳表中的示意图：

首先 randomLevel() 返回 3，表示需要建二级索引，即：一级索引和二级索引需要增加元素 6。该跳表目前最高三级索引，首先找到三级索引的 1，发现 6 比 1大比 13小，所以，从 1 下沉到二级索引。

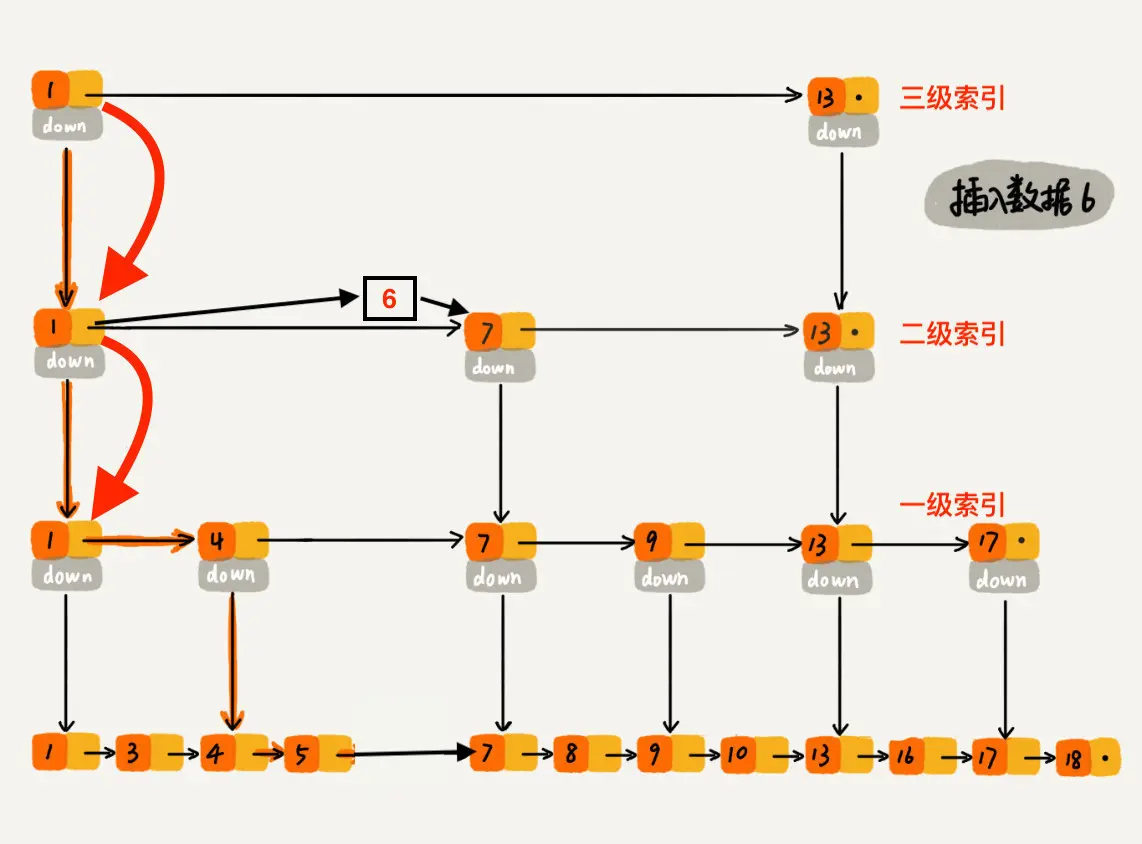
下沉到二级索引后，发现 6 比 1 大比 7 小，此时需要在二级索引中 1 和 7 之间加一个元素6 ，并从元素 1 继续下沉到一级索引。

下沉到一级索引后，发现 6 比 1 大比 4 大，所以往后查找，发现 6 比 4 大比 7 小，此时需要在一级索引中 4 和 7 之间加一个元素 6 ，并把二级索引的 6 指向 一级索引的 6（在当前 Demo 中，二级索引和一级索引是一个结点，所以没有这一步），最后，从元素 4 继续下沉到原始链表。

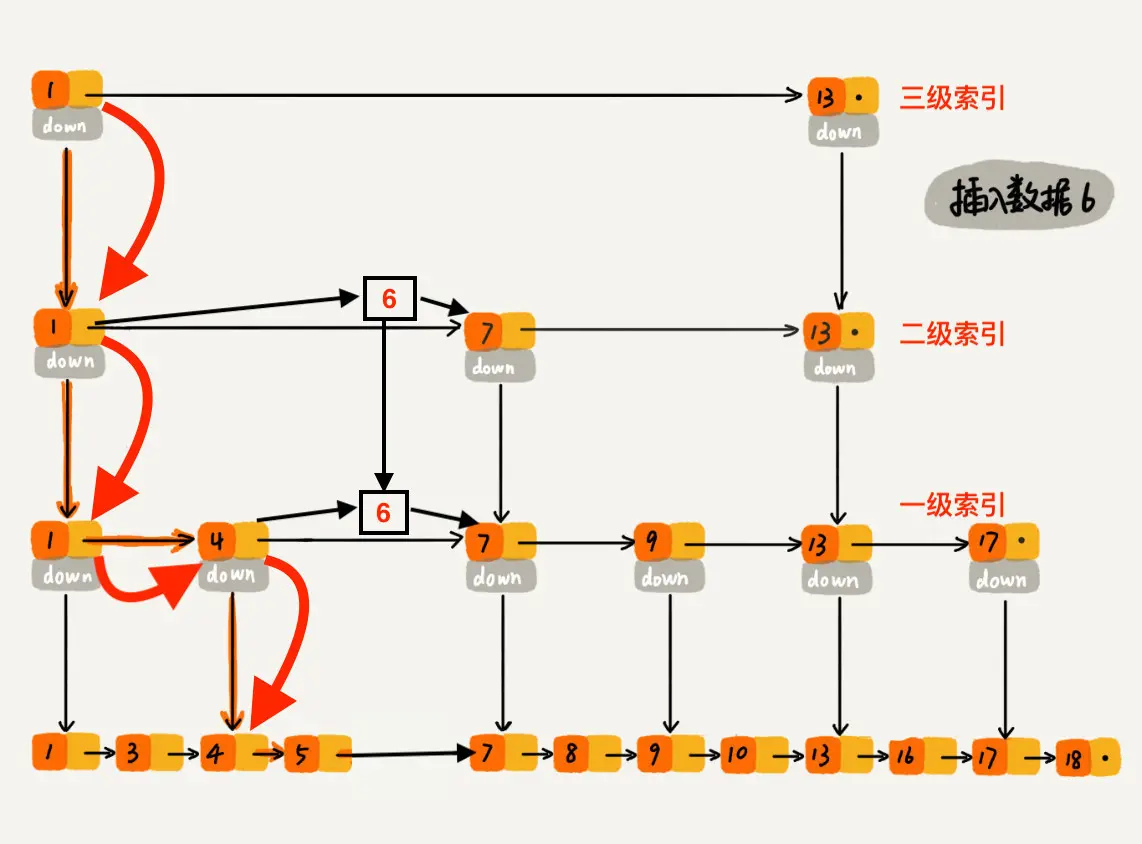
下沉到原始链表后，就比较简单了，发现 4、5 比 6小，7比6大，所以将6插入到 5 和 7 之间即可，整个插入过程结束。

完整的 Demo 实现，传送门

六、LeetCode 题目

∞、参考链接