链表（Linked List）

链表是一种物理存储单元上非连续、非顺序的存储结构，链表中的元素使用指针链接。

链表由 N 个节点组成的，每一个节点就是一个对象，每一个节点分为两部分：

• 数据域（用于存储数据）
• 指针域（用于连接各个链表）

注意：头结点不存储数据，其数据域一般无意义（当然有些情况下也可存放链表的长度、用做监视哨等等）。

为何引入头结点？

1. 对链表的删除、插入操作时，第一个结点的操作更方便；

   如果链表没有头结点，那么头指针指向的是链表的第一个结点，当在第一个结点前插入一个节点时，那么头指针要相应指向新插入的结点，把第一个结点删除时，头指针的指向也要更新。也就是说如果没有头结点，我们需要维护着头指针的指向更新，因为头指针指向的是链表的第一个结点。如果引入头结点的话，那么头结点的 next 始终都是链表的第一个结点。

2. 统一空表和非空表的处理

   有了头结点之后头指针指向头结点，不论链表是否为空，头指针总是非空，而且头结点的设置使得对链表的第一个位置上的操作与在表中其它位置上的操作一致，即统一空表和非空表的处理。

头指针和头结点的区别？

链表中第一个结点的存储位置叫做头指针。头结点是为了操作的统一与方便而设立的，放在第一个元素结点之前。链表中可以没有头结点，但不能没有头指针。如果链表有头结点，那么头指针是指向头结点的指针，如果没有头结点，那么头指针就是指向第一个元素结点的指针。

有头结点的单链表结构：

无头结点的单链表结构：

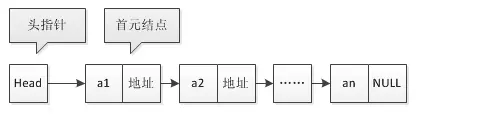
可以分为以下几种类型的链表：

一、单链表（Singly Linked List）

1.1 代码实现

节点结构

public class Node <E> {
    private Node<E> next;

    private E e;
}

单向链表类

public class SingleLinkedList { 
    // 声明头节点
    private Node<E> head;
    // 声明尾节点
    private Node<E> tail;
    // 链表的大小
    private int size;

    /**
     * 获取单链表中存储的元素总数
     * 
     * @return 返回 size 属性
     */
    public int size() {
        return size;
    }
}

增加

public void add(E e) {
    // 以 e 实例化一个节点
    Node<E> node = new Node<E>(e);
    // 往尾节点后加节点
    tail.setNext(node);
    // 该节点设为最后一个节点
    tail = node;
    size++;
}

删除

/**
 * 删除指定的节点 e，并返回 e
 */
public E delete(int index) {

    if (index < 0 || index > size)
        return null;
    if (index == 0) { // 当索引为 1 时，令头节点的下一个节点为头节点
        Node<E> node2 = head.getNext();
        head.setNext(node2.getNext());
        size--;
        return node2.getE();
    }
    // 获取要删除节点的前一个节点
    Node<E> bNode = select(index - 1);
    // 获取要删除的节点
    Node<E> node = bNode.getNext();
    // 获取要删除节点的后一个节点
    Node<E> nNode = Node.getNext();

    // 先建立删除节点的前一个节点和删除节点的后一个节点的关系
    bNode.setNext(nNode);
    // 清除 node 的下一个节点
    node.setNext(null);
    size--;
    // 返回删除节点中的数据域
    return node.getE();
}

修改

/**
 * 修改指点位置的数据域
 */
public E update(E x, int index) {
    if (index < 0 || index > size || size == 0)
        return null;
    Node<E> xnode = new Node<E>(x); // 获取一个新节点
    Node<E> node = select(index);
    node.setE(xnode.getE());
    return node.getE();
}

访问（Access）

/**
 * 获取指定索引位置的节点对象
 */
private Node<E> select(int index) {
    // 将头节点的下一个节点赋给 node
    Node<E> node = head.getNext();
    for (int i = 0; i < index; i++) {
        // 获取 node 的下一个节点
        node = node.getNext();
    }
    return node;
}

/**
 * 获取指定索引位置的节点数据域
 */
public E getE(int index) {
    if (index < 0 || index > size - 1)
        return null;
    // 查找指定索引位置的节点对象
    Node<E> node = select(index);
    return node.getE();
}

搜索（Search）

访问和搜索有什么区别？

• Access: get A[i] element value，也就是根据指定索引位置获取节点对象或节点数据；
• Search: find whether some value exists in array (and get it's index)，也就是根据指定数据判断该数据是否存在于链表中，并返回索引。

1.2 复杂度

• 时间复杂度：
  • 访问（Access）：O(n)
  • 查找（Search）：O(n)
  • 插入（Add）：O(1)（指定节点）或 O(n)（指定索引）
  • 删除（Delete）：O(n)
• 空间复杂度：O(n)

1.3 使用场景

单链表适用于需要按顺序存储和处理数据的场景，如文件系统、堆栈等。由于单链表的插入和删除操作相对简单，因此在实现动态数组时也经常使用单链表。

二、双链表（Doubly Linked List）

• 与单链表对比，双链表需要多一个指针用于指向前驱节点，因此如果存储同样多的数据，双向链表要比单链表占用更多的内存空间；
• 双链表的插入和删除需要同时维护 next 和 prev 两个指针；
• 双链表中的元素访问需要通过顺序访问，支持双向遍历，这就是双向链表操作的灵活性根本。

2.1 代码实现

注：以下是只有头尾指针，没有头尾结点的写法。

节点结构

public class Node {
    int data;
    Node prev;
    Node next;

    public Node(int data)
    {
	this.data = data; 
	this.prev = null; 
	this.next = null; 
    }
}

双向链表类

public class DoublyLinkedList { 
    Node head; 
    Node tail; 

    public DoublyLinkedList() 
    { 
	this.head = null; 
	this.tail = null; 
    } 
}

添加

• 在链表开头插入（O(1)）

public void insertAtBeginning(int data) {
    Node temp = new Node(data);
    if (head == null) {
	// 当前链表为空，头尾指针都指向新插入的结点
	head = temp;
	tail = temp;
    } else {
	temp.next = head;
	head.prev = temp;
	head = temp;
    }
}

• 在链表指定位置插入（O(n)）

public void insertAtPosition(int data, int position) { 
    Node temp = new Node(data); 
    if (position == 1) { 
	insertAtBeginning(data);
    } else {
	Node current = head; 
	int currPosition = 1;
	// 找到待插入位置对应的结点
	while (current != null && currPosition < position) { 
	    current = current.next; 
	    currPosition++; 
	}

	if (current == null) {
	    insertAtEnd(data); 
	} else {
	    temp.next = current;
	    temp.prev = current.prev;
	    current.prev.next = temp;
	    current.prev = temp;
	}
    }
}

• 在链表末尾插入（O(1)）

public void insertAtEnd(int data) {
    Node temp = new Node(data);
    if (tail == null) {
        // 当前链表为空，头尾指针都指向新插入的结点
	head = temp;
	tail = temp;
    } else {
	tail.next = temp;
	temp.prev = tail;
	tail = temp;
    }
}

删除

• 删除链表中的第一个节点（O(1)）

public void deleteAtBeginning() {
    if (head == null) {
	return;
    }

    // 当前链表只有一个结点
    if (head == tail) {
	head = null;
	tail = null;
	return;
    }

    // 需要注意第一个节点被删除后，next 要置空
    Node temp = head;
    head = head.next;
    head.prev = null;
    temp.next = null;
}

• 删除链表中指定位置的节点（O(n)）

public void delete(int pos) { 
    if (head == null) {
	return;
    }

    if (pos == 1) {
	deleteAtBeginning();
	return;
    }

    Node current = head;
    int count = 1;

    // 找到待删除位置对应的结点
    while (current != null && count != pos) {
	current = current.next;
	count++;
    }

    // 指定位置的结点不存在
    if (current == null) {
	System.out.println("Position wrong");
	return;
    }

    if (current == tail) {
	deleteAtEnd();
	return;
    }

    current.prev.next = current.next;
    current.next.prev = current.prev;
    current.prev = null;
    current.next = null;
}

• 删除链表中的最后一个节点（O(1)）

public void deleteAtEnd() { 
    if (tail == null) {
	return;
    }

    // 当前链表只有一个结点
    if (head == tail) {
	head = null;
	tail = null;
	return;
    }

    // 需要注意最后一个节点被删除后，prev 要置空
    Node temp = tail;
    tail = tail.prev;
    tail.next = null;
    temp.prev = null;
}

• 删除链表指定节点（O(1)）

public void delete(Node node) { 
    if (node == null) {
	    return;
    }

    // 这是第一个结点
    if (node.prev == null) {
	    deleteAtBeginning();
	    return;
    }

    // 这是最后一个结点
    if (node.next == null) {
        deleteAtEnd();
        return;
    }

    node.prev.next = node.next;
    node.next.prev = node.prev;
    node.prev = null;
    node.next = null;
}

修改

访问（Access）

搜索（Search）

2.2 复杂度

• 时间复杂度：
  • 访问（Access）：O(n)
  • 查找（Search）：O(n)
  • 插入（Add）：O(1)（指定节点）或 O(n)（指定索引）
  • 删除（Delete）：O(1)（指定节点）或 O(n)（指定索引）
• 空间复杂度：O(n)

2.3 使用场景

双向链表非常适合程序中的撤消（Undo）和重做（Redo）等功能，因为你可以在操作中前进和后退。

1. Web Browsing
2. Social Media Apps
3. Video Streaming Platforms
4. Board Games
5. Audio Books

双链表效率比单链表高，为什么还要保留单链表呢，甚至单链表的应用比双链表还要广泛？

1. 单链表更简单，单链表的学习成本要双链表低，而且学习了单链表就能更好的理解双链表；
2. 存储效率，每个双链表的节点要比单链表的节点多一个指针，也就意味着更高的内存开销，如果你对于效率和内存开销，更在意的是内存开销，又或者你的程序就没有指定节点插入或删除的操作，那这时候就可以用单链表。

三、循环链表（Circular Linked List）

3.1 代码实现

...

3.2 复杂度

3.3 使用场景

循环链表适用于需要循环遍历的场景，如环形缓冲区、轮询调度等。由于循环链表的最后一个节点指向头节点，因此在实现循环队列时也经常使用循环链表。

四、双循环链表（Doubly Circular linked list）

4.1 代码实现

节点结构

public class Node <E> {
    private Node<E> pre; // 指向上一个节点

    private Node<E> next; // 指向下一个节点

    private E e; // 数据域
}

附加信息：头节点、链表长度等

    // 声明头节点
    private Node<E> head;
    // 链表的大小
    private int size;

    /**
     * 获取单链表中存储的元素总数
     * 
     * @return 返回 size 属性
     */
    public int size() {
        return size;
    }

链表初始化：

public DoublyLinkedList() {
    /**
     * 头结点不存储值，并且头结点初始化时，就一个头结点。（伪头结点）
     */
    head = new Node<>(null, null, null);
    head.pre = head.next;
    head = head.next;
    size = 0;
}

增加

/**
 * 添加元素（尾部插入）
 *
 * @param e 节点值
 */
public void add(E e) {
    Node<E> cur = new Node<>(head.pre, head, e);
    /*
    1、新节点的前一个节点的后一个节点为新节点；
    2、新节点的后一个节点的前一个节点是新节点；
     */
    head.pre.next = cur;
    head.next = cur;
    size++;
    return;
}

/**
 * 添加元素（头部插入）
 *
 * @param e 节点值
 */
public void addToHead(E e) {
    Node<E> cur = new Node<>(head, head.next, e);
    head.next.pre = cur;
    head.next = cur;
    size++;
    return;
}

删除

/**
 * 根据索引删除元素
 *
 * @param index 待删除节点对应的索引
 */
public void delete(int index) {
    Node<E> cur = get(index);
    cur.pre.next = cur.next;
    cur.next.pre = cur.pre;
    size--;
    // 释放当前节点
    cur = null;
    return;
}

public void deleteHead() {
    delete(0);
}

public void deleteTail() {
    delete(size - 1);
}

修改

访问

搜索

4.2 复杂度

4.3 使用场景

五、Leetcode 题目

• 2. 两数相加

∞、参考链接

• Types of Linked List
• Introduction to Doubly Linked Lists in Java
• What are real life examples of Double Linked List?
• 看动画轻松理解「链表」实现「LRU缓存淘汰算法」