B Plus Tree - tenji/ks GitHub Wiki
B+ 树是 B 树数据结构的一种变体。在 B+ 树中,数据指针仅存储在树的叶节点处。在 B+ 树中,叶节点的结构与内部节点的结构不同。叶节点对于搜索字段(Key)的每个值都有一个条目,以及指向记录(或包含该记录的块)的数据指针。B+ 树的叶节点链接在一起,以提供对记录的搜索字段的有序访问。B+ 树的内部节点用于指导搜索。叶节点中的一些搜索字段值在 B+ 树的内部节点中重复。
没有一篇论文单独介绍 B+ 树的概念。相反,在叶节点中维护所有数据的概念被反复提出,作为 B 树的一个有趣变体,由 R. Bayer 和 E. McCreight 引入。Douglas Comer 在对 B 树(也包括 B+ 树)的早期调查中指出,B+ 树用于 IBM 的 VSAM 数据访问软件,并引用了 1973 年 IBM 发表的一篇文章。
可以参考 B 树的特性:传送门

B+ 树包含两种类型的节点:
- 内部节点(Internal Nodes):
- 叶子节点(Leaf Nodes):叶节点是具有 n 个指针的节点。
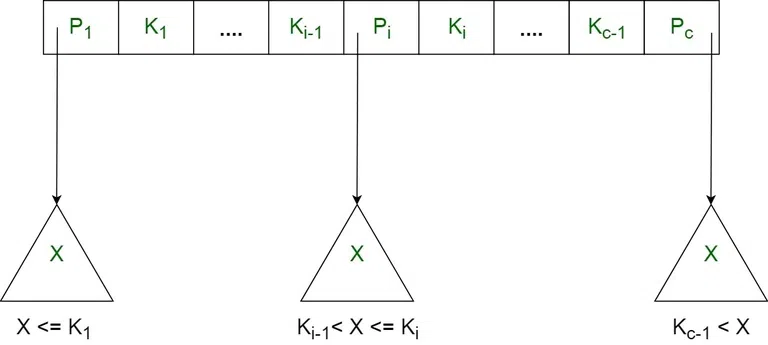
- 每个内部节点的形式如下: <P1, K1, P2, K2, ….., Pc-1, Kc-1, Pc> 其中 c <= a 并且每个 Pi 是一个树指针(即指向树),每个 Ki 都是一个键值;
- 对于 Pi 指向的子树中的每个搜索字段值
X,以下条件成立:Ki-1 < X <= Ki,对于 1 < I < c 且 Ki-1 < X,对于 i = c; - 每个内部节点最多有
a个树指针; - 根节点至少有两个树指针,而其他内部节点每个至少有
$ceil(a/2)$ 个树指针; - 如果内部节点有
c个指针,c <= a,则它有c – 1个键值。
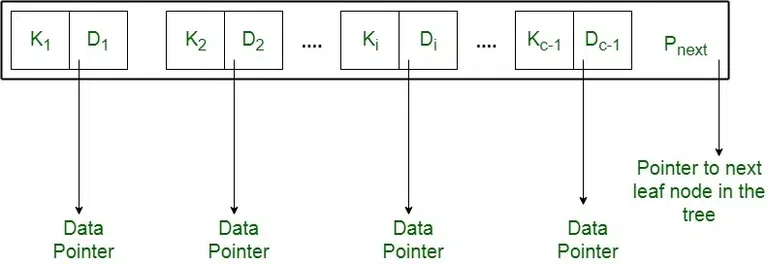
- 每个叶节点的形式为: <<K1, D1>, <K2, D2>, ….., <Kc-1, Dc-1>, Pnext> 其中 c <= b 并且每个 Di 是一个数据指针 (即指向磁盘中键值为 Ki 的实际记录或包含该记录的磁盘文件块),并且每个 Ki 是一个键值,Pnext 指向 B+ 树中的下一个叶子节点;
- 每个叶节点至少有
$ceil(b/2)$ 个值; - 所有叶节点都处于同一级别。
数据库存储引擎中使用 B+ 树实现的索引结构简单示意图:
// B+ Tree class with basic operations: insert and search
class BPlusTree {
// Root node of the tree
private BPlusTreeNode root;
// Maximum number of keys per node
private final int order;
// Constructor to initialize the B+ Tree
public BPlusTree(int order) {
if (order < 3) {
throw new IllegalArgumentException("Order must be at least 3");
}
this.root = new BPlusTreeNode(true);
this.order = order;
}
...
}// B+ Tree Node class to represent
// internal and leaf nodes
class BPlusTreeNode {
// True for leaf nodes, False for internal nodes
boolean isLeaf;
// The keys stored in this node
List<Integer> keys;
// Children nodes (for internal nodes)
List<BPlusTreeNode> children;
// Link to the next leaf node
BPlusTreeNode next;
// Constructor to initialize a node
public BPlusTreeNode(boolean isLeaf) {
this.isLeaf = isLeaf;
this.keys = new ArrayList<>();
this.children = new ArrayList<>();
this.next = null;
}
}方法流程:
- 找到需要插入的 Key 所在的叶子节点;
- 将 Key 插入所在叶子节点的 Key 数组;
- 判断所在叶子节点的 Key 数量是否已经大于 m - 1(m 是 B+ 树的阶数),大于的话需要分割叶子节点,否则流程结束;
- 如果该叶子节点是根节点,则生成一个新的根节点,流程结束;如果不是,需要将 Key 插入父节点(也就是内部节点);
- 如果父节点(也就是内部节点)Key 数量不大于 m - 1(m 是 B+ 树的阶数),则流程结束;
- 如果父节点 Key 数量大于 m - 1,需要分割父节点,分割父节点和分割叶子结点流程一致。
// Insert a key into the B+ Tree
public void insert(int key) {
BPlusTreeNode leaf = findLeaf(key);
insertIntoLeaf(leaf, key);
// Split the leaf node if it exceeds the order
if (leaf.keys.size() > order - 1) {
splitLeaf(leaf);
}
}
// Find the appropriate leaf node for insertion
private BPlusTreeNode findLeaf(int key) {
BPlusTreeNode node = root;
while (!node.isLeaf) {
int i = 0;
while (i < node.keys.size() && key >= node.keys.get(i)) {
i++;
}
node = node.children.get(i);
}
return node;
}
// Insert into the leaf node
private void insertIntoLeaf(BPlusTreeNode leaf, int key) {
int pos = Collections.binarySearch(leaf.keys, key);
if (pos < 0) {
pos = -(pos + 1);
}
leaf.keys.add(pos, key);
}
// Split a leaf node and update parent nodes
private void splitLeaf(BPlusTreeNode leaf) {
int mid = (order + 1) / 2;
BPlusTreeNode newLeaf = new BPlusTreeNode(true);
// Move half the keys to the new leaf node
newLeaf.keys.addAll(leaf.keys.subList(mid, leaf.keys.size()));
leaf.keys.subList(mid, leaf.keys.size()).clear();
newLeaf.next = leaf.next;
leaf.next = newLeaf;
// If the root splits, create a new root
if (leaf == root) {
BPlusTreeNode newRoot = new BPlusTreeNode(false);
newRoot.keys.add(newLeaf.keys.get(0));
newRoot.children.add(leaf);
newRoot.children.add(newLeaf);
root = newRoot;
} else {
insertIntoParent(leaf, newLeaf, newLeaf.keys.get(0));
}
}
// Insert into the parent node after a leaf split
private void insertIntoParent(BPlusTreeNode left, BPlusTreeNode right, int key) {
BPlusTreeNode parent = findParent(root, left);
if (parent == null) {
throw new RuntimeException("Parent node not found for insertion");
}
int pos = Collections.binarySearch(parent.keys, key);
if (pos < 0) {
pos = -(pos + 1);
}
parent.keys.add(pos, key);
parent.children.add(pos + 1, right);
// Split the internal node if it exceeds the order
if (parent.keys.size() > order - 1) {
splitInternal(parent);
}
}
// Split an internal node
private void splitInternal(BPlusTreeNode internal) {
int mid = (order + 1) / 2;
BPlusTreeNode newInternal = new BPlusTreeNode(false);
// Move half the keys to the new internal node
newInternal.keys.addAll(internal.keys.subList(mid + 1, internal.keys.size()));
internal.keys.subList(mid, internal.keys.size()).clear();
// Move half the children to the new internal node
newInternal.children.addAll(internal.children.subList(mid + 1, internal.children.size()));
internal.children.subList(mid + 1, internal.children.size()).clear();
// If the root splits, create a new root
if (internal == root) {
BPlusTreeNode newRoot = new BPlusTreeNode(false);
newRoot.keys.add(internal.keys.get(mid));
newRoot.children.add(internal);
newRoot.children.add(newInternal);
root = newRoot;
} else {
insertIntoParent(internal, newInternal, internal.keys.remove(mid));
}
}
// Find the parent node of a given node
private BPlusTreeNode findParent(BPlusTreeNode current, BPlusTreeNode target) {
if (current.isLeaf || current.children.isEmpty()) {
return null;
}
for (int i = 0; i < current.children.size(); i++) {
BPlusTreeNode child = current.children.get(i);
if (child == target) {
// Parent found
return current;
}
BPlusTreeNode possibleParent = findParent(child, target);
if (possibleParent != null) {
return possibleParent;
}
}
// Parent not found
return null;
}方法流程:
- 找到该 Key 所在的叶子节点;
- 对于该叶子节点中的 Key 数组,执行二分查找,返回查找结果。
// Search for a key in the B+ Tree
public boolean search(int key) {
BPlusTreeNode node = findLeaf(key);
int pos = Collections.binarySearch(node.keys, key);
return pos >= 0;
}
// Find the appropriate leaf node for insertion
private BPlusTreeNode findLeaf(int key) {
BPlusTreeNode node = root;
while (!node.isLeaf) {
int i = 0;
while (i < node.keys.size() && key >= node.keys.get(i)) {
i++;
}
node = node.children.get(i);
}
return node;
}// Display the Tree (for debugging purposes)
public void printTree() {
printNode(root, 0);
}
private void printNode(BPlusTreeNode node, int level) {
System.out.println("Level " + level + ": " + node.keys);
if (!node.isLeaf) {
for (BPlusTreeNode child : node.children) {
printNode(child, level + 1);
}
}
}完整的 Demo 实现,传送门
B+ 树广泛应用于需要高效索引和快速检索的应用中,包括:
- 关系数据库的数据库索引;
- 高效搜索、插入和删除至关重要的文件系统结构;
- 需要通过范围查询排序数据的应用程序,例如内存数据库或缓存。
- B+ 树的层级更少:相较于 B 树,B+ 每个非叶子节点存储的关键字数更多,树的层级更少所以查询数据更快;
- B+ 树的查询速度更稳定:B+ 所有关键字数据地址都存在叶子节点上,所以每次查找的次数都相同所以查询速度要比 B 树更稳定;
- B+ 树天然具备排序功能::B+ 树所有的叶子节点数据构成了一个有序链表,在查询大小区间的数据时候更方便,数据紧密性很高,缓存的命中率也会比 B 树高;
- B+ 树全节点遍历更快:B+ 树遍历整棵树只需要遍历所有的叶子节点即可,而不需要像 B 树一样需要对每一层进行遍历,这有利于数据库做全表扫描。
| Aspect | B-Tree | B+ Tree |
|---|---|---|
| Structure | Separate leaf nodes for data storage and internal nodes for indexing | Nodes store both keys and data values |
| Leaf Nodes | Leaf nodes form a linked list for efficient range-based queries | Leaf nodes do not form a linked list |
| Order | Higher order (more keys) | Lower order (fewer keys) |
| Key Duplication | Typically allows key duplication in leaf nodes | Usually does not allow key duplication |
| Disk Access | Better disk access due to sequential reads in a linked list structure | More disk I/O due to non-sequential reads in internal nodes |
| Applications | Database systems, file systems, where range queries are common | In-memory data structures, databases, general-purpose use |
| Performance | Better performance for range queries and bulk data retrieval | Balanced performance for search, insert, and delete operations |
| Memory Usage | Requires more memory for internal nodes | Requires less memory as keys and values are stored in the same node |
索引数据一般是存储在磁盘中的,但是计算数据都是要在内存中进行的,如果索引文件很大的话,并不能一次都加载进内存,所以在使用索引进行数据查找的时候是会进行多次磁盘 IO,将索引数据分批的加载到内存中,因此一个好的索引的数据结构,在得到正确的结果前提下,一定是磁盘 IO 次数最少的。另外,根节点是常驻内存的。
另外,MySQL 是支持范围查找的,所以索引的数据结构不仅要能高效地查询某一个记录,而且也要能高效地执行范围查找。也就是说,MySQL 的索引需要满足下面的条件:
- 能在尽可能少的磁盘的 I/O 操作中完成查询工作;(B+ 树的层级更少,因此更适合)
- 要能高效地查询某一个记录,也要能高效地执行范围查找;(B+ 树的叶子节点数据构成了一个有序链表,范围查找、排序查找效率更高)
数据库存储引擎中使用 B+ 树实现的索引结构(带模拟数据)示意图待补充...
为什么不选择 Hash 作为索引?
目前 MySQL 其实是有两种索引数据类型可以选择的,一个是 B-Tree(实际是B+ Tree)、一个是 Hash。但是为什么在实际的使用过程中,基本上大部分都是选择 B+ Tree 呢?主要原因是:
- 但是像
select * from Table where id > 15这种范围查询,Hash 类型的索引就搞不定了,对这种范围查询,会直接全表扫描,另外 Hash 类型的索引也搞不定排序; - 还有就是虽然 MySQL 底层做了一系列的处理,但还是不能完全的保证,不产生 Hash 碰撞。
MySQL 数据库单表超过两千万行记录就需要分表?原理是什么?