树、二叉树 - suzhouzc/Data-Structure GitHub Wiki
-
二叉树的性质
1、设非空的二叉树中度为0、1、2的结点个数分别为n0、n1和n2,则n0=n2+1(叶子结点比二分支结点多一个)
2、二叉树第i层至多有2^(i-1)个结点(i>=1);m叉树第i层至多有m^(i-1)个结点(i>=1);
3、高度为h的m叉树至多有(m^h-1)/m-1个结点; 高度为h的二叉树至多有2^h-1个结点
4、具有n个(n>0)个结点的完全二叉树的深度为 (1、向下取整 2、向上取整)
5、
-
先序遍历(递归)
Void PreOrder(BiTree T){
if (T!=NULL){
visit(T);
PreOrder(T->lchild);
PreOrder(T->rchild);
}
}
非递归
void PreOrder2 (BiTree T){
InitStack(S);BiTree p=T;
while (p||!IsEmpty(S)){
if (p){
visit(p);
Push(S,p);
p=p->lchild;
}
else{
Pop(S,p);
p=p->rchild
}
}
}
-
中序遍历(递归)
void InOrder (BiTree T){
if (T!=NULL){
InOrder(T->lchild);
visit(T);
InOrder(T->rchild);
}
}
(非递归)
void InOrder2(BiTree T){
InitStack(S); BiTree p=T;
while(p||!IsEmpty(S)){
if(p){
Push(S,p);
p=p->lchild;
}
else{
Pop(S,p);
visit(p);
p=p->rchild;
}
}
}
-
后序遍历(递归)
void PostOrder(BiTree T){
if(!T=NULL){
PostOrder(T->lchild);
PostOrder(T->rchild);
visit(T);
}
}
(非递归)
void PostOrder2(BiTree T){
InitStack(S);
BiTree p=T;
while(p||!IsEmpty(S)){
if(p){
Push(S,p);
p=p->lchild;
}
else{
GetTop(S,p); //读取栈顶的结点(非出栈)
if(p->rchild&&p->rchild!=r){ //若右子树存在,且未被访问过
p=p->rchild;
}
else{
Pop(S,p);
visit(p);
r=p;//记录最近访问过的结点
p=NULL;
}
}
}
}
-
层次遍历
void LevelOrder(BiTree T){
LinkQueue Q;
InitQueue(Q); BiTree p;
EnQueue(Q,T);
while(!IsEmpty (Q)){ //队列不空则循环
DeQueue(Q,p);
visit(p);
if(p->lchild!=NULL)
EnQueue(Q,p->lchild);
if(p->rchild!=NULL)
EnQueue(Q,p->rchild);
}
}

typedef struct ThreadNode{
ElemType data;
struct ThreadNode *lchild,*rchild;
int Ltag,rtag;
}ThreadNode,*ThreadTree;
-
用双亲表示法(好处:方便找到根结点从而方便并与查)
双亲表示法:每个结点中保存指向双亲的“指针”。
#define MAX_TREE_SIZE 100
typedef struct{
ElemType data;
int parent;
}PTNode;
typedef struct{
PTNode nodes[MAX_TREE_SIZE]; //双亲的表示
int n; //结点数
}PTree;
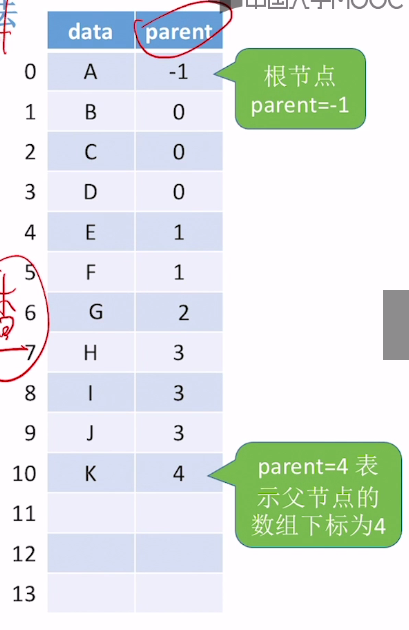
-
并查集结构
#define SIZE 13
int UFSets[SIZE]; //集合元素的数组
//初始化并查集
void Initial(int S[]){
for(int i=0;i<SIZE;i++)
S[i]=-1;
}
-
查操作
int Find(int S[],int x){
while(S[x]>=0)
x=S[x];
return x; //时间复杂度:最坏的情况下:O(n) 优化Union后的最坏的情况下:O(log2^n) Union的最坏合并n个是O(n*log2^n)
}
-
并操作
void Union(int S[],int Root1,int Root2){
if(Root1==Root2) return; //要求Root1与Root2是不同的集合
S[Root2]=Root1; //将根Root2连接到另一根Root1下面 时间复杂度: O(1)
}
*并操作优化 :Union“并”操作,小树合并到大树 //将n个合并时O(n^2) 单个是0(1) 用根节点的绝对值表示一棵树(集合)的结点总数、Union操作合并两棵树时,小树并入大树
void Union(int S[],int Root1,int Root2){
if(Root1==Root2) return;
if(S[Root2]>S[Root1]){ //S[]里的数值为负数
S[Root1]+=S[Root2];
S[Root2]=Root1; //小树Rooot2合并到大树Root1;
}
else{
S[Root2]+=S[Root1];
S[Root1]=Root2;
}
}
-
并操作优化 :Find“查”操作:压缩路径:先找到根节点,再将查找路径上所有结点都挂到根节点下 几乎等于O(1);是小于等于O(4); Union的最坏合并n个是O(n*4);
int Find(int S[],int x){
int root=x;
while(S[root]>=0) root=S[root];
while(x!=root){ //压缩路径 将该路径上的所有结点都遍历一遍并且都挂在根节点下
int t=S[x]; //t指向x的父节点
S[x]=root; //x直接挂到根节点下
x=t;
}
return root; //返回根节点编号
}