Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apple.

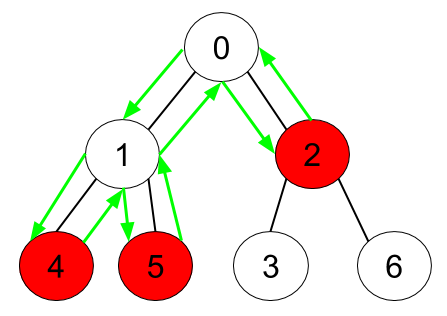
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8 
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

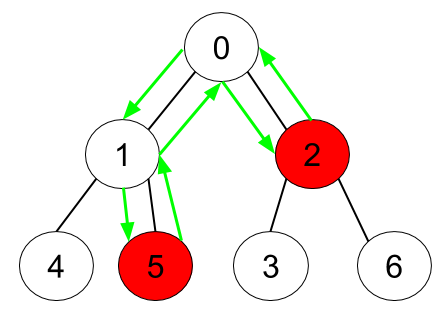
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0

1 <= n <= 105
edges.length == n - 1
edges[i].length == 2
0 <= ai < bi <= n - 1
hasApple.length == n

• Create an adjacency list where adj[X] contains all the neighbors of node X.
• Start a DFS traversal.
• We use a function dfs to perform the traversal. For each call, pass node, parent, adj, hasApple as the parameters. The dfs would return the time to collect all the apples in node's subtree. We start with node 0 and parent as -1.
• Mark the node as visited.
• Create a variable totalTime to store the time required to collect all the apples in the node's subtree. Initalize it with 0.
• Create another variable childTime to store time required to collect all the apples for each immediate child of node. Intialize it with 0.
• Iterate over all the children of the node (nodes that share an edge) and check if any child is equal to the parent. If the child is equal to the parent, we will not visit it again.
• If the child is not equal to the parent, recursively call the dfs with node as child and parent as node. At the end of dfs traversal, we have the time required to collect all the apples in its subtree. Store it in childTime.
• If the child has an apple (hasApple[child] = true) or there are any apples in its subtree, which can be checked if we need any time to collect apples (childTime > 0), we must visit child, which takes one unit of time, collect all apples in the child's subtree which takes childTime, and return, which again takes one unit of time. So, we add childTime + 2 to the totalTime.
• If neither the child nor its subtree has apples, we don't need to include the time to visit this child, as we will consider we never visited this child's subtree.
• At the end of dfs traversal for node 0, we have the time required to collect the apples in the subtree of node 0.

class Solution {
    public int dfs(int node, int parent, Map<Integer, List<Integer>> adj,
            List<Boolean> hasApple) {
        if (!adj.containsKey(node))
            return 0;

        int totalTime = 0, childTime = 0;
        for (int child : adj.get(node)) {
            if (child == parent)
                continue;
            childTime = dfs(child, node, adj, hasApple);
            // childTime > 0 indicates subtree of child has apples. Since the root node of the
            // subtree does not contribute to the time, even if it has an apple, we have to check it
            // independently.
            if (childTime > 0 || hasApple.get(child))
                totalTime += childTime + 2;
        }
        return totalTime;
    }

    public int minTime(int n, int[][] edges, List<Boolean> hasApple) {
        Map<Integer, List<Integer>> adj = new HashMap<>();
        for (int[] edge : edges) {
            int a = edge[0], b = edge[1];
            adj.computeIfAbsent(a, value -> new ArrayList<Integer>()).add(b);
            adj.computeIfAbsent(b, value -> new ArrayList<Integer>()).add(a);
        }
        return dfs(0, -1, adj, hasApple);
    }
}

Here, n be the number of nodes.

Time complexity: O(n)

Each node is visited by the dfs function once, which takes O(n) time in total. We also iterate over the edges of every node once (since we don't visit a node more than once, we don't iterate its edges more than once), which adds O(n) time since we have n−1 edges. We also require O(n) time to initialize the adjacency list and the visit array. Space complexity: O(n)

The recursion call stack used by dfs can have no more than n elements in the worst-case scenario. It would take up O(n) space in that case. We also require O(n) space for the adjacency list and the visit array.