Given a 2D integer array nums, return all elements of nums in diagonal order as shown in the below images.

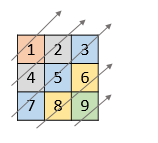
Input: nums = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,4,2,7,5,3,8,6,9]

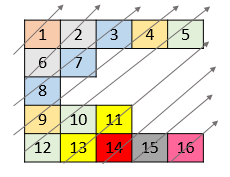
Input: nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]]
Output: [1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]

1 <= nums.length <= 105
1 <= nums[i].length <= 105
1 <= sum(nums[i].length) <= 105
1 <= nums[i][j] <= 105

The crux of the problem is figuring out how to identify the diagonals and how to iterate over them. We will make use of an important property of diagonals in this approach.

Let's say you are currently at the start of a diagonal (bottom-left) and your coordinates are row, col. How do you get to the next value in the diagonal? You go up and right. By going up, you move to row - 1. By going right, you move to col + 1. That is, our row decreases by 1, and our col increases by 1.

This is true for any given point in any given diagonal. If we were to consider the sum row, col, it would be constant along the diagonal since the -1 from moving up cancels out the +1 from moving right!

As you can see in the above image, every square is annotated with row + col. Each diagonal shares the same values.

For each square, we will use the sum row + col as an identifier to the diagonal that it belongs to. We will use a hash map groups where groups[x] is a list of all values that appear in the diagonal with identifier x.

To collect the cells on each diagonal in the correct order, we will iterate through each row from left to right starting with the bottom row. The reason we choose the bottom-up, left-to-right order is that the diagonals move upward and to the right, so by iterating to the upper right, we will visit the squares in the correct order.

Once we have populated groups, we simply need to iterate over the identifiers and add each list to our answer. Notice that conveniently, the order in which we visit the diagonals is the same as the identifier order! What we mean by this is that the first diagonal we traverse is 0, then 1, then 2, and so on.

Thus, we can use an integer curr initialized to 0 that represents the current diagonal we are adding to our answer. We add groups[curr] to the answer, then increment curr, and repeat until curr is no longer in groups.

class Solution {
    public int[] findDiagonalOrder(List<List<Integer>> nums) {
        HashMap<Integer, List<Integer>> groups = new HashMap<>();
        int n=0;
        for(int i=nums.size()-1;i>=0;i--){
            for(int j=0;j<nums.get(i).size();j++){
                int diagonal = i+j;
                if(!groups.containsKey(diagonal)){
                    groups.put(diagonal,new ArrayList<Integer>());
                }
                groups.get(diagonal).add(nums.get(i).get(j));
                n++;
            }
        }
        int[] ans = new int[n];
        int i = 0;
        int curr = 0;
        
        while (groups.containsKey(curr)) {
            for (int num : groups.get(curr)) {
                ans[i] = num;
                i++;
            }
            
            curr++;
        }
        
        return ans;
    }
}

Given n as the number of integers in grid,

Time complexity: O(n)

We iterate over each of the n integers to populate groups, then we iterate over them again to populate ans.

Space complexity: O(n)

The values of groups are lists that together will store exactly n integers, thus using O(n) space.

The same can also be achieved using BFS algorithm

In the previous approach, we require two passes. The first pass populates groups, and the second pass populates ans. Can we do better, perhaps solving the problem in one pass?

Yes! Let's think about the grid as a graph. Each square is a node, and we can imagine each node having an edge to the squares below and to the right (if they exist). Let's take a look at the diagonal image again:

As you can see, a node with identifier x has edges to nodes with identifier x + 1. If we consider the top-left square 0, 0 as a "source" node, then each square's identifier is exactly equal to its distance from the source. This allows us to visit the diagonals in order using BFS!

We start a BFS from 0, 0. At each node row, col, we first push row + 1, col to the queue and then row, col + 1. Note that we only add a square to the queue if it both exists and has not been visited yet.

How do we know if a square has been visited yet? We could use a hash set to keep track of visited squares, but there is a simpler way. We only need to consider the square row + 1, col (down) if we are at the start of a diagonal. Otherwise, for every other square on the diagonal, the square below it has already been visited by the right edge of the previous square.

class Solution {
    public int[] findDiagonalOrder(List<List<Integer>> nums) {
        Queue<Pair<Integer, Integer>> queue = new LinkedList();
        queue.offer(new Pair(0, 0));
        List<Integer> ans = new ArrayList();
        
        while (!queue.isEmpty()) {
            Pair<Integer, Integer> p = queue.poll();
            int row = p.getKey();
            int col = p.getValue();
            ans.add(nums.get(row).get(col));
            
            if (col == 0 && row + 1 < nums.size()) {
                queue.offer(new Pair(row + 1, col));
            }
            
            if (col + 1 < nums.get(row).size()) {
                queue.offer(new Pair(row, col + 1));
            }
        }
        
        // Java needs conversion
        int[] result = new int[ans.size()];
        int i = 0;
        for (int num : ans) {
            result[i] = num;
            i++;
        }
        
        return result;
    }
}

Given n as the number of integers in grid,

Time complexity: O(n)

During the BFS, we visit each square once, performing O(1) work at each iteration.

Space complexity: O( n ​ )

The extra space we use is for queue. The largest size queue will be is proportional to the size of the largest diagonal.