Convert Sorted List to Binary Search Tree - shilpathota/99-leetcode-solutions GitHub Wiki
Given the head of a singly linked list where elements are sorted in ascending order, convert it to a height-balanced binary search tree.
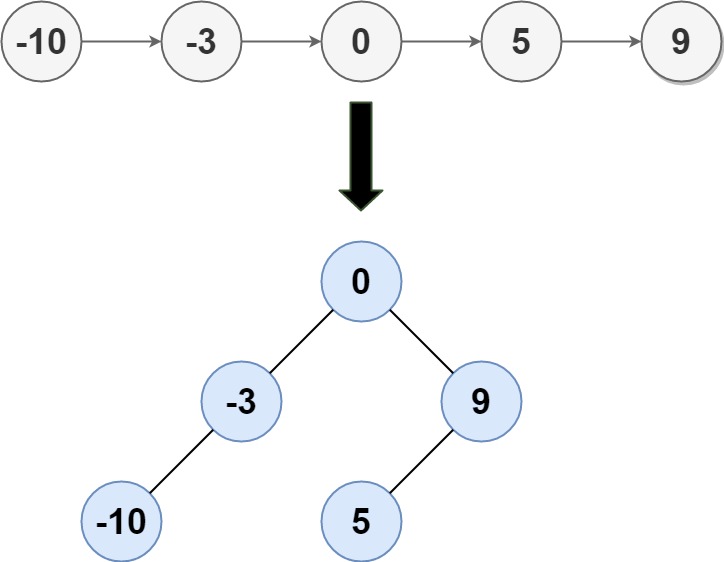
Input: head = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: One possible answer is [0,-3,9,-10,null,5], which represents the shown height balanced BST.
Input: head = []
Output: []
The number of nodes in head is in the range [0, 2 * 104].
-105 <= Node.val <= 105
- Since we are given a linked list and not an array, we don't really have access to the elements of the list using indexes. We want to know the middle element of the linked list.
- We can use the two pointer approach for finding out the middle element of a linked list. Essentially, we have two pointers called slow_ptr and fast_ptr. The slow_ptr moves one node at a time whereas the fast_ptr moves two nodes at a time. By the time the fast_ptr reaches the end of the linked list, the slow_ptr would have reached the middle element of the linked list. For an even sized list, any of the two middle elements can act as the root of the BST.
- Once we have the middle element of the linked list, we disconnect the portion of the list to the left of the middle element. The way we do this is by keeping a prev_ptr as well which points to one node before the slow_ptr i.e. prev_ptr.next = slow_ptr. For disconnecting the left portion we simply do prev_ptr.next = None
- We only need to pass the head of the linked list to the function that converts it to a height balances BST. So, we recurse on the left half of the linked list by passing the original head of the list and on the right half by passing slow_ptr.next as the head.
/**
* Definition for singly-linked list. public class ListNode { int val; ListNode next; ListNode(int
* x) { val = x; } }
*/
/**
* Definition for a binary tree node. public class TreeNode { int val; TreeNode left; TreeNode
* right; TreeNode(int x) { val = x; } }
*/
class Solution {
private ListNode findMiddleElement(ListNode head) {
// The pointer used to disconnect the left half from the mid node.
ListNode prevPtr = null;
ListNode slowPtr = head;
ListNode fastPtr = head;
// Iterate until fastPr doesn't reach the end of the linked list.
while (fastPtr != null && fastPtr.next != null) {
prevPtr = slowPtr;
slowPtr = slowPtr.next;
fastPtr = fastPtr.next.next;
}
// Handling the case when slowPtr was equal to head.
if (prevPtr != null) {
prevPtr.next = null;
}
return slowPtr;
}
public TreeNode sortedListToBST(ListNode head) {
// If the head doesn't exist, then the linked list is empty
if (head == null) {
return null;
}
// Find the middle element for the list.
ListNode mid = this.findMiddleElement(head);
// The mid becomes the root of the BST.
TreeNode node = new TreeNode(mid.val);
// Base case when there is just one element in the linked list
if (head == mid) {
return node;
}
// Recursively form balanced BSTs using the left and right halves of the original list.
node.left = this.sortedListToBST(head);
node.right = this.sortedListToBST(mid.next);
return node;
}
}Time Complexity: O(NlogN)
Space Complexity: O(logN). Since we are resorting to recursion, there is always the added space complexity of the recursion stack that comes into picture. This could have been O(N) for a skewed tree, but the question clearly states that we need to maintain the height balanced property. This ensures the height of the tree to be bounded by O(logN). Hence, the space complexity is O(logN).
You can get the time complexity down by using more space.
- Convert the given linked list into an array. Let's call the beginning and the end
- Convert the given linked list into an array. Let's call the beginning and the end of the array as left and right
- Find the middle element as (left + right) / 2. Let's call this element as mid. This is a O(1) time operation and is the only major improvement over the previous algorithm.
- The middle element forms the root of the BST.
- Recursively form binary search trees on the two halves of the array represented by (left, mid - 1) and (mid + 1, right) respectively.
- Let's look at the implementation for this algorithm and then we will get to the complexity analysis.of the array as left and right
- Find the middle element as (left + right) / 2. Let's call this element as mid. This is a O(1) time operation and is the only major improvement over the previous algorithm.
- The middle element forms the root of the BST.
- Recursively form binary search trees on the two halves of the array represented by (left, mid - 1) and (mid + 1, right) respectively.
- Let's look at the implementation for this algorithm and then we will get to the complexity analysis.
/**
* Definition for singly-linked list. public class ListNode { int val; ListNode next; ListNode(int
* x) { val = x; } }
*/
/**
* Definition for a binary tree node. public class TreeNode { int val; TreeNode left; TreeNode
* right; TreeNode(int x) { val = x; } }
*/
class Solution {
private List<Integer> values;
public Solution() {
this.values = new ArrayList<Integer>();
}
private void mapListToValues(ListNode head) {
while (head != null) {
this.values.add(head.val);
head = head.next;
}
}
private TreeNode convertListToBST(int left, int right) {
// Invalid case
if (left > right) {
return null;
}
// Middle element forms the root.
int mid = (left + right) / 2;
TreeNode node = new TreeNode(this.values.get(mid));
// Base case for when there is only one element left in the array
if (left == right) {
return node;
}
// Recursively form BST on the two halves
node.left = convertListToBST(left, mid - 1);
node.right = convertListToBST(mid + 1, right);
return node;
}
public TreeNode sortedListToBST(ListNode head) {
// Form an array out of the given linked list and then
// use the array to form the BST.
this.mapListToValues(head);
// Convert the array to
return convertListToBST(0, this.values.size() - 1);
}
}Time Complexity: The time complexity comes down to just O(N) now since we convert the linked list to an array initially and then we convert the array into a BST. Accessing the middle element now takes O(1) time and hence the time complexity comes down.
Space Complexity: Since we used extra space to bring down the time complexity, the space complexity now goes up to O(N) as opposed to just O(logN) in the previous solution. This is due to the array we construct initially.
We know that the leftmost element in the inorder traversal has to be the head of our given linked list. Similarly, the next element in the inorder traversal will be the second element in the linked list and so on. This is made possible because the initial list given to us is sorted in ascending order.
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private ListNode head;
private int findSize(ListNode head){
if(head == null) return 0;
int c =0;
while(head!=null){
head=head.next;
c++;
}
return c;
}
private TreeNode convertList(int l, int r){
if(l>r) return null;
int mid = (l+r)/2;
TreeNode left = this.convertList(l,mid-1);
TreeNode node = new TreeNode(this.head.val);
node.left = left;
this.head=this.head.next;
node.right = this.convertList(mid+1,r);
return node;
}
public TreeNode sortedListToBST(ListNode head) {
int size = this.findSize(head);
this.head = head;
return convertList(0,size-1);
}
}Time Complexity: The time complexity is still O(N) since we still have to process each of the nodes in the linked list once and form corresponding BST nodes.
Space Complexity: O(logN) since now the only extra space is used by the recursion stack and since we are building a height balanced BST, the height is bounded by logN.