Given a reference of a node in a connected undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.

class Node { public int val; public List neighbors; }

Test case format:

For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.

An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

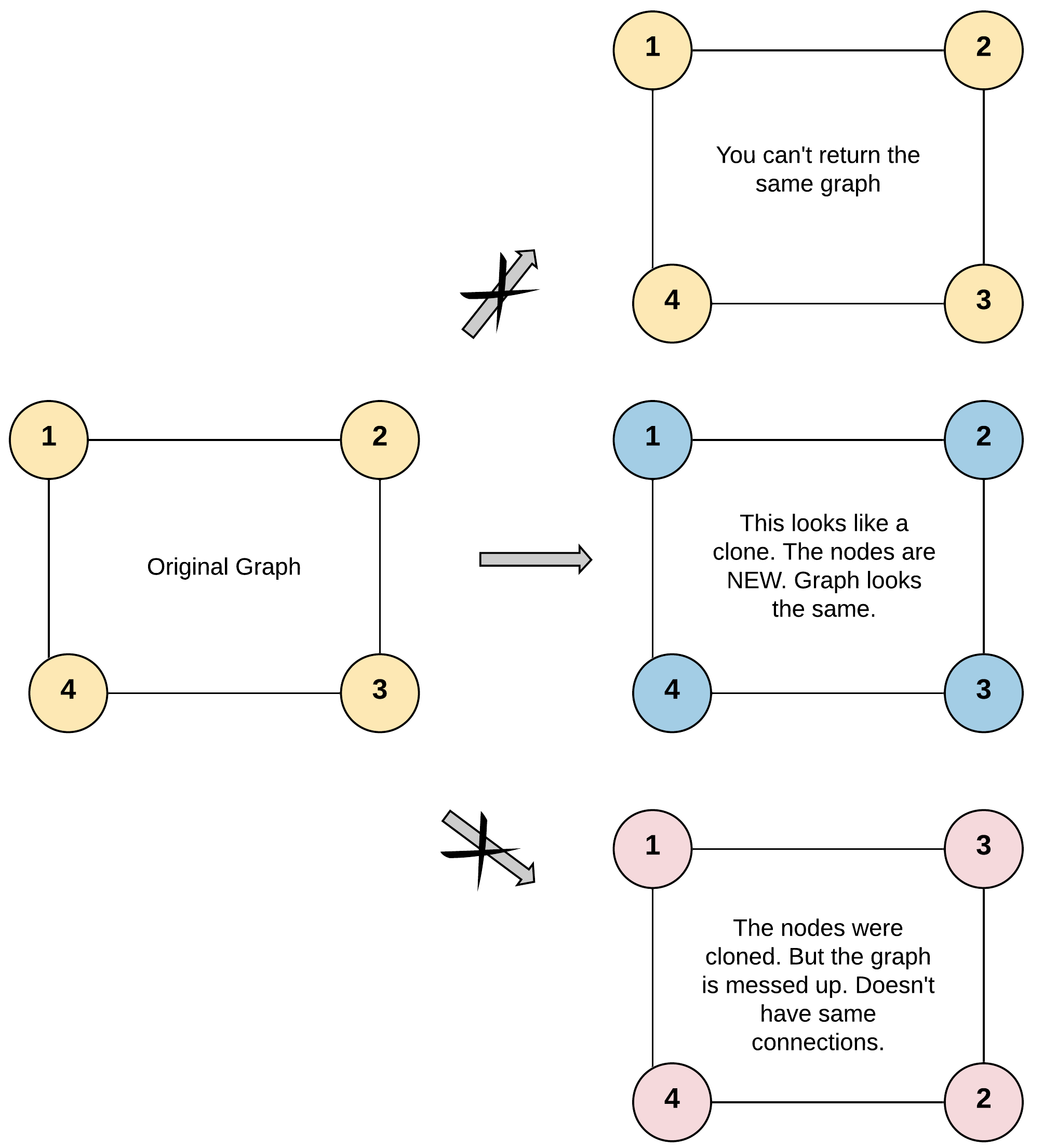
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).

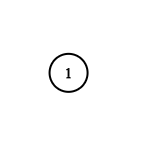
Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.

The number of nodes in the graph is in the range [0, 100].
1 <= Node.val <= 100
Node.val is unique for each node.
There are no repeated edges and no self-loops in the graph.
The Graph is connected and all nodes can be visited starting from the given node.

WE can use BFS algorithm for this approach

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> neighbors;
    public Node() {
        val = 0;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val) {
        val = _val;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val, ArrayList<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}
*/

class Solution {
    public Node cloneGraph(Node node) {
        if(node == null) return null;
        HashMap<Node,Node> visited = new HashMap();
        LinkedList<Node> queue = new LinkedList<Node>();
        queue.add(node);
        visited.put(node,new Node(node.val,new ArrayList<>()));
        while(!queue.isEmpty()){
            Node n = queue.remove();
            for(Node nei:n.neighbors){
                if(!visited.containsKey(nei)){
                    visited.put(nei,new Node(nei.val,new ArrayList<>()));
                    queue.add(nei);
                }
                visited.get(n).neighbors.add(visited.get(nei));
            }
        }
        return visited.get(node);
    }
}

Time Complexity : O(N+M), where N is a number of nodes (vertices) and M is a number of edges.

Space Complexity : O(N). This space is occupied by the visited dictionary and in addition to that, space would also be occupied by the queue since we are adopting the BFS approach here. The space occupied by the queue would be equal to O(W) where W is the width of the graph. Overall, the space complexity would be O(N).