The boundary of a binary tree is the concatenation of the root, the left boundary, the leaves ordered from left-to-right, and the reverse order of the right boundary.

The left boundary is the set of nodes defined by the following:

The root node's left child is in the left boundary. If the root does not have a left child, then the left boundary is empty. If a node in the left boundary and has a left child, then the left child is in the left boundary. If a node is in the left boundary, has no left child, but has a right child, then the right child is in the left boundary. The leftmost leaf is not in the left boundary. The right boundary is similar to the left boundary, except it is the right side of the root's right subtree. Again, the leaf is not part of the right boundary, and the right boundary is empty if the root does not have a right child.

The leaves are nodes that do not have any children. For this problem, the root is not a leaf.

Given the root of a binary tree, return the values of its boundary.

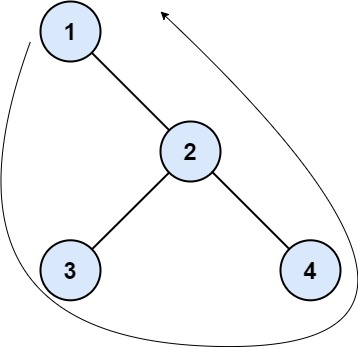
Input: root = [1,null,2,3,4]
Output: [1,3,4,2]
Explanation:
- The left boundary is empty because the root does not have a left child.
- The right boundary follows the path starting from the root's right child 2 -> 4.
  4 is a leaf, so the right boundary is [2].
- The leaves from left to right are [3,4].
Concatenating everything results in [1] + [] + [3,4] + [2] = [1,3,4,2].

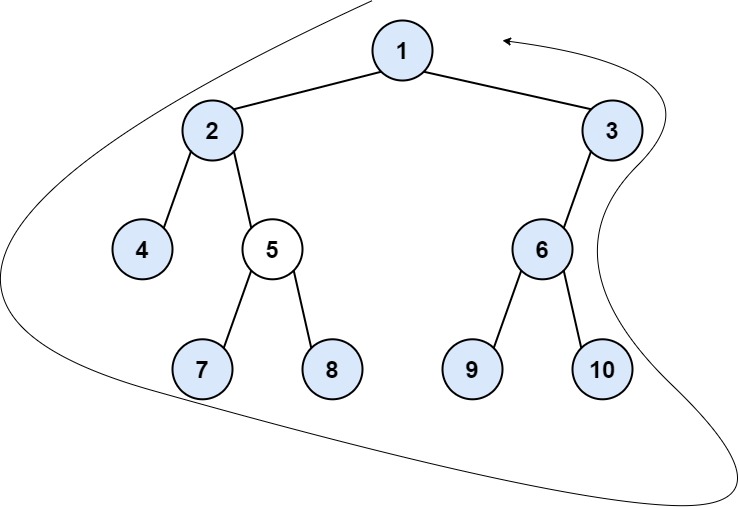
Input: root = [1,2,3,4,5,6,null,null,null,7,8,9,10]
Output: [1,2,4,7,8,9,10,6,3]
Explanation:
- The left boundary follows the path starting from the root's left child 2 -> 4.
  4 is a leaf, so the left boundary is [2].
- The right boundary follows the path starting from the root's right child 3 -> 6 -> 10.
  10 is a leaf, so the right boundary is [3,6], and in reverse order is [6,3].
- The leaves from left to right are [4,7,8,9,10].
Concatenating everything results in [1] + [2] + [4,7,8,9,10] + [6,3] = [1,2,4,7,8,9,10,6,3].

The number of nodes in the tree is in the range [1, 104].
-1000 <= Node.val <= 1000

• The main function boundaryOfBinaryTree initiates the boundary extraction process by checking if the root is not a leaf and adding it to the result list self.res.

• Next, it extracts the left boundary by iterating from the root's left child downwards, always preferring the left child for following. If no left child is present, it chooses the right child. Nodes verified as non-leaves are appended to the result list.

• A recursive helper function add_leaves is used to traverse the entire tree, and it adds leaf nodes' values to the result list.

• The right boundary is extracted in a similar way to the left boundary, but this time a temporary stack s is used to store the nodes' values for later reversal.

• After collecting all right boundary nodes in the stack, we pop the elements one by one and append them to our result list to maintain the reverse order required for the right boundary.

A simple utility function is_leaf determines whether a given node is a leaf by checking that it does not have any left or right children.

• The recursion strategy employed by add_leaves adds the benefit of an in-depth tree traversal to find all leaves. Starting from a node, if it is a leaf node (verified via the is_leaf function), its value is appended to self.res.
• Otherwise, the function recursively calls itself on the left child (if exists), then on the right child (if exists), effectively performing a pre-order traversal (since leaves must be collected from left to right as specified in the problem).

To address the requirement of adding the right boundary in reverse order, a stack data structure is introduced, which inherently reverses the order of elements as they are popped out. This approach neatly handles the reverse order without any additional logic or reverse traversal.

• Finally, after traversing the left boundary, adding leaves, and using the stack for the right boundary, the complete boundary list self.res is returned containing all boundary elements in the required order.
• The effective combination of iterative traversals for left and right boundaries, recursion for leaves, and stack for the reversal of the right boundary creates a comprehensive and clean solution for the boundary traversal problem.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
            List<Integer> output = new ArrayList<>();
    private void addLeaves(TreeNode node) {

      // A node is considered a leaf if it doesn't have any children.
        if (isLeaf(node)) {
            output.add(node.val);
            return;
        }
        // Process all left descendants.
        if (node.left != null) {
            addLeaves(node.left);
        }
        // Process all right descendants.
        if (node.right != null) {
            addLeaves(node.right);
        }
    }

    /**
     * Checks if a node is a leaf node.
     * @param node Node to check.
     * @return True if the node is a leaf, false otherwise.
     */
    private boolean isLeaf(TreeNode node) {
        return node.left == null && node.right == null;
    }
    public List<Integer> boundaryOfBinaryTree(TreeNode root) {
        if(root == null) return Collections.emptyList();
        if(!isLeaf(root)){
            output.add(root.val);
        }
       TreeNode current = root.left;
        while (current != null) {
            if (!isLeaf(current)) {
                output.add(current.val);
            }
            // Move to the left if possible; otherwise, move to the right.
            current = current.left != null ? current.left : current.right;
        }

        // Add all leaf nodes.
        addLeaves(root);

        // Right boundary in reverse order (excluding the last leaf node if any).
        Deque<Integer> stack = new ArrayDeque<>();
        current = root.right;
        while (current != null) {
            if (!isLeaf(current)) {
                stack.push(current.val);
            }
            // Move to the right if possible; otherwise, move to the left.
            current = current.right != null ? current.right : current.left;
        }
        // Add the right boundary nodes to the result while preserving their order.
        while (!stack.isEmpty()) {
            output.add(stack.pop());
        }


        return output;
    }
}

The time complexity of the provided function boundaryOfBinaryTree is O(n), where n is the number of nodes in the binary tree. This can be inferred due to the function add_leaves being a recursive call that will visit each node exactly once to check if it is a leaf. Additionally, the while loops to traverse the left and right boundaries of the tree will at most also touch each node once since they do not visit the same nodes as add_leaves.

The space complexity of this function can be primarily attributed to the space needed to store the result (self.res) and the recursion call stack when adding leaves. The list self.res and the stack s collectively can hold up to O(n) node values (where n is the number of leaves for self.res and the number of nodes in the right boundary for s). Furthermore, in the worst case of an extremely unbalanced tree, the space complexity for the recursion call stack could also reach O(n), so the total space complexity is O(n).