Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST):

BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST. boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false. int next() Moves the pointer to the right, then returns the number at the pointer. Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST.

You may assume that next() calls will always be valid. That is, there will be at least a next number in the in-order traversal when next() is called.

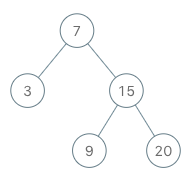
Input
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
Output
[null, 3, 7, true, 9, true, 15, true, 20, false]

Explanation
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next();    // return 3
bSTIterator.next();    // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 20
bSTIterator.hasNext(); // return False

The number of nodes in the tree is in the range [1, 105].
0 <= Node.val <= 106
At most 105 calls will be made to hasNext, and next.

Could you implement next() and hasNext() to run in average O(1) time and use O(h) memory, where h is the height of the tree?

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class BSTIterator {
    ArrayList<Integer> nodeSorted;
    int index;
    public BSTIterator(TreeNode root) {
        this.nodeSorted = new ArrayList<>();
        this.index = -1;
        this._inorder(root);
        
    }
    private void _inorder(TreeNode root){
        if(root==null) return;

        this._inorder(root.left);
        this.nodeSorted.add(root.val);
        this._inorder(root.right);
    }
    public int next() {
        return this.nodeSorted.get(++this.index);
    }
    
    public boolean hasNext() {
        return this.index+1 < this.nodeSorted.size();
    }
}

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator obj = new BSTIterator(root);
 * int param_1 = obj.next();
 * boolean param_2 = obj.hasNext();
 */

Time complexity : O(N) is the time taken by the constructor for the iterator. The problem statement only asks us to analyze the complexity of the two functions, however, when implementing a class, it's important to also note the time it takes to initialize a new object of the class and in this case it would be linear in terms of the number of nodes in the BST. In addition to the space occupied by the new array we initialized, the recursion stack for the inorder traversal also occupies space but that is limited to O(h) where h is the height of the tree.

next() would take O(1)

hasNext() would take O(1)

Space complexity : O(N) since we create a new array to contain all the nodes of the BST. This doesn't comply with the requirement specified in the problem statement that the maximum space complexity of either of the functions should be O(h) where h is the height of the tree and for a well balanced BST, the height is usually logN. So, we get great time complexities but we had to compromise on the space. Note that the new array is used for both the function calls and hence the space complexity for both the calls is O(N).