脱関数化を実用する 5 - shiatsumat/fp-papers GitHub Wiki

正規表現に対する伝統的な継続ベースのマッチャー [[26](脱関数化を実用する 8#reference26)] を考え、それを脱関数化して、脱関数化の前後で正当性証明 (correctness proof) を比較対照する。このために、[§5.1](脱関数化を実用する 5#section5-1) では正規表現とそれが表す言語をざっと振り返る。[§5.2](脱関数化を実用する 5#section5-2) では高階である継続ベースのマッチャーと、それを脱関数化したものを提示する。[§5.3](脱関数化を実用する 5#section5-3) では両者の正当性証明を比較対照する。

アルファベット Σ に対する正規表現 r の文法と、対応する言語 L(r) は以下の通りである。

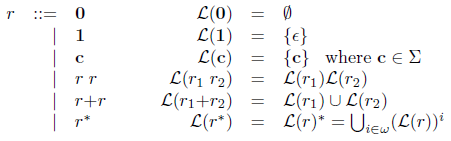
私たちは文字列を Haskell の文字のリストとして、正規表現を以下の Haskell のデータ型の要素として表す。

data RegExp = Zero
            | One
            | Char Char
            | Cat RegExp RegExp
            | Sum RegExp RegExp
            | Star RegExp

「正規表現の言語」に対応する概念を以下のように定義する。

• L(Zero) = {}
• L(One) = {[]}
• L(Char c) = {[c]}
• L(Cat r1 r2) = L(r1) L(r2)
• L(Sum r1 r2) = L(r1) ∪ L(r2)
• L(Star r) = ⋃_{i ∈ ω}(L(r))ⁱ

言語の結合は L₁ L₂ = {x++y | x ∈ L₁ ∧y ∈ L₂} として定義される（文字列結合のためにHaskellで++と書かれる付加 (append) 関数を使っている）。［(L(r))ⁱ は L(r)L(r)…L(r) と i 回続くものを表す。ω は非負整数全体の集合である。更に以下において ⋃_{i ∈ ω}(L(r))ⁱ を L(r)^＊ と略記する。］

正規表現に対する参照マッチャーの1つは高階である（[図1](脱関数化を実用する 5#fig1)）。そしてそれを脱関数化したものを提示する（[図2](脱関数化を実用する 5#fig2)）。

図1：高階の継続ベースの正規表現マッチャー

accept, accept_star :: (RegExp, [Char], [Char] -> Bool) -> Bool
accept (r, s, k) = case r of
    Zero      -> False
    One       -> k s
    Char c    -> case s of
        (c':s') -> c == c' && k s'
        []      -> False
    Cat r1 r2 -> accept (r1, s, \s' -> accept (r2, s', k))
    Sum r1 r2 -> accept (r1, s, k) || accept (r2, s, k)
    Star r'   -> accept_star (r', s, k)
accept_star (r, s, k)
    = k s || accept (r, s, \s' -> s /= s' && accept_star (r, s', k))

match :: (RegExp, [Char]) -> Bool
match (r, s) = accept (r, s, \s' -> s' == [])

図1は、合成的で継続ベースの私たちの参照マッチャーを示している。合成的というのは、acceptの再帰呼び出しすべてが正規表現の考えられている正規な部分 (proper subpart) に対して行われているということである。継続ベースというのは、マッチャーの制御の流れが継続でなされているということである。

メインの関数はmatchである。この関数は正規表現と文字列のリストを与えられると、その正規表現とリストと、文字列のリストを受け取り空かどうか確かめる最初の継続とともに、acceptを呼び出すのである。

accept関数は、文字列のリストを縫うように進みながら入力の正規表現を再帰的に下降する。

accept_star関数は、Starの枝でローカルに定義された、再帰的継続のラムダ持ち上げされた (lambda-lifted) バージョンである。（この状況は命令型言語でのwhileループのある合成的な解釈器と全く同じである。whileループではループを解釈するための補助的な再帰関数を書けるのである。）この再帰的継続は、マッチングが文字列中で進行していることを確かめる。

最近、ハーパーは「証明指向のデバッグ」の良い例となる同様のマッチャーを発表した。彼はふざけてクリーネスターをマッチしているときに進行をチェックしない非合成的マッチャーを考えた。彼の記事は (1) 構造的帰納法による証明を試みるときに非合成的な部分でどうつまずくか、そして (2) Star Oneのような病的な正規表現に対してマッチャーが発散するとどのように気付くか、を示している。そしてハーパーは (1) マッチャーを合成的にして (2) 病的な正規表現が除かれるように正規表現を正規化 (normalize) した。代わりに、合成的なマッチャーから始めて、accept_starに進行テストを含めて、病的な正規表現を扱えるようにしよう。

図2：一階のスタックベースの正規表現マッチャー

data RegExpStack = Empty
                 | Accept RegExp RegExpStack
                 | AcceptStar [Char] RegExp RegExpStack

accept_def, accept_star_def :: (RegExp, [Char], RegExpStack) -> Bool
accept_def (r, s, k) = case r of
    Zero      -> False
    One       -> pop_and_accept (k, s)
    Char c    -> case s of
        (c':s') -> c == c' && pop_and_accept (k, s')
        []      -> False
    Cat r1 r2 -> accept_def (r1, s, Accept r2 k)
    Sum r1 r2 -> accept_def (r1, s, k) || accept_def (r2, s, k)
    Star r'   -> accept_star_def (r', s, k)
accept_star_def (r, s, k)
    = pop_and_accept (k, s) || accept_def (r, s, AcceptStar s r k)

pop_and_accept :: (RegExpStack, [Char]) -> Bool
pop_and_accept (Empty, s')            = s' == []
pop_and_accept (Accept r2 k, s')      = accept_def (r2, s', k)
pop_and_accept (AcceptStar s r k, s') = s /= s' && accept_star_def (r, s', k)

[図1](脱関数化を実用する 5#fig1)のマッチャーを脱関数化すると、継続を表すデータ型と関連する適用関数が生まれる。

このデータ型は正規表現のスタックを表している。このスタックにはクリーネスターでのテストのための副状況 (side condition) があるかもしれない。適用関数は単純にこのスタックの一番上の要素をポップしてそれを文字列の残りの部分とマッチさせようとする。ゆえにデータ型をRegExpStackと名付け、適用関数をpop_and_acceptと名付ける。また、データ構成子に意味のある名前を与えている。[図2](脱関数化を実用する 5#fig2)はその結果を示している。

高階のバージョンと一階のバージョンの両方に正当性証明を与えて、それぞれの証明が他方のバージョンの証明へと変換できるかどうかを調べる。

ここで選ぶ正当性の基準は単純に任意の正規表現rと文字列s（文字のリストで表される）について

• match (r, s)の評価が停止し、かつ match (r, s) ~> True ⇔ s ∈ L(r) である

ということである。match (r, s) ~> True と書いたのは、match (r, s)を評価すると停止しTrueという結果が得られるということを意味している。さらに私たちは Haskell のプログラムについて等式的に推論し、e と e' が等しいと（関数定義によって）定義されているとき e ≡ e' と書くことにする。もし e ≡ e' ならば e と e' は何らかの同じ値へと評価され、e ~> v ⇔ e' ~> v となる。Haskell の式について、同じ値を表しているときに限り e = e' と書くことにする。

定義により match (r, s) ≡ accept (r, s, \s' -> s' == []) であるので、上の任意のsとrと、sの任意の接尾辞 (suffix) について停止する文字のリストからブール値への任意の関数kについて、

• accept (r, s, k)の評価が停止し、かつ accept (r, s, k) ~> True ⇔ s ∈ L(r)L(k) である

ということを証明すれば十分である。ただし、「文字列受容関数」kの言語 L(k) を集合 {s | k s ~> True} として定義している。

その証明は正規表現上の構造的帰納法 (structural induction) である。r = Star r' である場合、部分証明は任意の文字列について以下のことが満たされるということを示す。

• accept_star (r', s, k)の評価が停止し、かつ accept_star (r', s, k) ~> True ⇔ s ∈ L(r')^＊L(k) である

この部分証明は、⇐ の方向には文字列の構造上（接尾辞を取ると小さくなる）における整礎帰納法 (well-founded induction) によって証明され、⇒ の方向には s ∈ L(r')ⁿL(k) であるような自然数nにおける数学的帰納法によって証明される。両方の部分証明はaccept (r', s, k)に対する外側の帰納法の仮定を用いる。（付録Aを参照せよ。）

この証明を脱関数化されたバージョンに持ち込むことができる。k sはpop_and_accept (k, s)へと翻訳されるので、L(k) を {s | pop_and_accept (k, s) ~> True} として定義する。そのあとの証明は全く同じ形式で進む。

代わりに、一階のマッチャーに対して直接の正当性証明を与えたければ、スタックkを関数を表すものと見なすという意気込みは小さくなるだろう。代わりに、以下の3つの命題を相互帰納法によって証明するだけで簡単に済ませることができる。

• P₁(r,s,k) ≜ accept (r, s, k) ~> True ⇔ s ∈ L(r)L(k)
• P₂(k,s) ≜ pop_and_accept (k, s) ~> True ⇔ s ∈ L(r)L(k)
• P₃(r,s,k) ≜ accept_star (r, s, k) ~> True ⇔ s ∈ L(r)^＊L(k)

ただし正規表現のスタックの言語は以下のように定義する。［∖ は差集合を表す。］

• L(Empty) = {[]}
• L(Accept (r, k)) = L(r)L(k)
• L(AcceptStar (s, r, k)) = (L(r)^＊L(k)) ∖ {s}

簡潔さのために証明の停止性の部分は無視し、全ての関数が全域的であると仮定する。命題自体に対する整礎帰納法により P₁,P₃,P₃ がs,r,kの任意の選択について成り立つことを証明する。ここで用いる順序は、辞書順で並んだ ω×ω への入り組んだ写像であり、証明はより「小さい」命題のみに依存するようにしている。（付録Bを参照せよ。）

この証明は高階のものよりも以下の2つの理由で複雑である。

1. 継続の言語をそれとマッチさせる関数と分離するので、関数が本当に正しい言語にマッチするかを確かめねばならない。

2. 高階の証明の2つのネストした帰納法を一つの整礎帰納法へと組み合わせねばならない。

それでもこの証明は高階のバージョンの継続の性質を明らかにする。その性質というのは、高々3種類の継続しか使われていないということで、これは継続の型――関数空間全体――からは見えてこない。

ゆえにこの関数空間の部分集合を、3つの抽象から生成される関数のみを含むように、帰納的に定義できる。一階の証明は、継続kがどこでもこの部分構造の中にあると仮定し、新しく生成される継続もそうだと示すことにより、高階のプログラムへと拡張される。事実上、継続の集合は、一階のデータ型が和を表すのと同様、疎な部分集合へと区分けされ、それぞれの部分の要素についての事柄を証明できるのだ。

一階のマッチャーの正当性証明は、継続を表す帰納的に定義されたデータ型が和であるという事実を直接用いている。この型の任意の値について、対偶を取ってそれぞれの場合について証明することができる。命題が3つの可能な部分のそれぞれについて成立するということを示し、この命題がその型のいかなる値についても成り立つに違いないと結論付けるのだ。これは脱関数化を彷彿させる。脱関数化では、プログラム全体で関数空間を占めている関数が全て、有限和で表されるプログラム中の関数抽象から生成されるからである。

私たちは一階のマッチャーの証明を翻訳して高階のマッチャーの証明へと直接翻訳することができる。結果として得られる証明は大域的な推論を行っている。つまり、使われる関数は全て有限個の関数抽象のみから生まれていて、さらにこれらの関数抽象は関数空間のある部分集合を帰納的に定義しているのである。［註：このような大域的な推論は、制御フロー解析によって可能になるものである [[46](脱関数化を実用する 8#reference46)]。］帰納法の仮定を変えて、関数が全てその部分構造から取られていると仮定する。関数抽象を実体化するとき、その結果が部分集合に属していること――そのことは自由変数における推論から従う――を示さねばならず、そうすることで初めてこの新しい関数において帰納法の仮定を用いることができるのである。関数を使うとき、対偶を取って場合分けによってこの関数の性質を示す。それぞれの場合はこの関数を作りうる抽象と対応している。命題が3つの可能な関数抽象のそれぞれについて成り立つということを示し、命題がその関数について成り立つに違いないと結論付ける。

高階のマッチャーの正当性証明は代わりに局所的な推論を使う。私たちは、それらの関数抽象によって生成される関数空間の部分集合に、関数がちょうど属しているということを仮定しない。その代わりに、任意の文字列について関数がその文字の全ての接尾辞について停止するという、より弱い性質を仮定する。この仮定は証明を完成するのには十分なのだ。

関数抽象をデータ構成子に、関数適用を適用関数の呼び出しに変えることによって、高階のマッチャーの証明を一階のマッチャーの証明へ直接翻訳することができる。結果として得られる証明は局所的な推論を使う。つまり定義される関数すべてが性質を満たしているのである。関数kが現在の文字列の全ての接尾辞について停止するという性質は、もしs'が現在の文字列の接尾辞ならばpop_and_accept (k, s')が停止するという性質へと翻訳できる。この仮定はpop_and_acceptの呼び出しまで伝わる。

したがって、2つの証明は再帰的推論の起こる場所が違うのである。

• 一階の場合、データ型の値についての再帰的推論は値が使用される時点において行われる。対照的に、データ型の値が定義される場所では推論がなされない。

• 高階の場合、関数の値についての再帰的推論は値が定義される時点において行われる。対照的に、関数の値が使われる場所では推論がなされない。

この違いは証明の間の翻訳によって強調される。2つのマッチャーで再帰を異なる扱い方をすることからこの違いは生じている。一階の場合、再帰は値が使われるケースディスパッチにおいて扱われる。高階の場合、再帰は関数抽象において扱われる。そして関数が定義される場所においてのみ関数抽象を手に入れて推論することができるのだ。

正規表現に対するマッチャーを、高階の形と一階の形の両方で考え、両者を比較し、両者の正当性証明を比較した。関数ベースとデータ型ベースの継続の表し方の違いは、代数的意味論における「ガラクタ (junk)」の概念を彷彿させる [[22](脱関数化を実用する 8#reference22)]。一方の表現は完全な関数空間であり多くの要素が実際の継続と対応しておらず、他方の表現は実際の継続に対応する要素のみを含む。この違いは、[§5.4](脱関数化を実用する 5#section5-4) で分析したように、2つのマッチャーの正当性証明に影響をもたらしている。

より一般的に言えば、このセクションはバックトラッキングのある言語のための、成功継続を使う関数型の解釈器を脱関数化することで1つのスタックを持つ再帰的解釈器が生まれるということも示している [[13](脱関数化を実用する 8#reference13),[31](脱関数化を実用する 8#reference31),[41](脱関数化を実用する 8#reference41)]。同様に、成功継続と失敗継続を使う関数型の解釈器を脱関数化することで2つのスタックを持つ反復的解釈器が生まれる [[13](脱関数化を実用する 8#reference13),[34](脱関数化を実用する 8#reference34)]。