脱関数化を実用する 4 - shiatsumat/fp-papers GitHub Wiki

このセクションでは、2つの構文論に対する解釈器を与える [[19](脱関数化を実用する 8#reference19),[57](脱関数化を実用する 8#reference57)]。1つは単純な算術式のためのものであり、もう一方は値渡しのラムダ計算のためのものである。これらの解釈器の両方が脱関数化の出力と対応しているということを私たちは見ていく。その後、対応する高階の継続渡しスタイルの解釈器を与える。それぞれの解釈器において、継続は対応する構文論の評価環境を表している。

私たちは、算術式の単純化された言語について考える。算術式は値（リテラル）と計算とのどちらかである。計算は足し算と第一引数が0かどうかを確かめる条件式とのどちらかである。

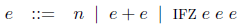
構文論は、値と評価環境とリデックス (redex) を定義することで、式の間の縮約関係を与える [[19](脱関数化を実用する 8#reference19)]。

値はリテラルであり、評価環境は次のように定義される。

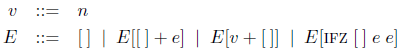
式 e の環境 E への差し込み（E[e] と書かれる）は次のように定義される。

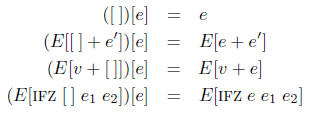
そして縮約関係は以下の規則で定義される。左辺の環境に差し込まれた式はリデックスと呼ばれる。

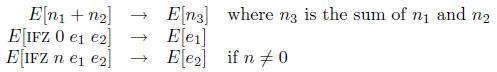
これらの定義は「一意分解」の補題 [[19](脱関数化を実用する 8#reference19),[57](脱関数化を実用する 8#reference57)] を満たしている。値でない任意の式 e は e = E[r] であるような評価環境 E とリデックス r に分解できるという補題である。

算術式は以下のデータ型を使って定義される。

data Aexp = Val Int   -- 些細な項
          | Comp Comp -- 重要な項
data Comp = Add Aexp Aexp
          | IfZ Aexp Aexp Aexp

Aexpでは、些細な項、つまり値（リテラル）と、重要な項、つまり計算（足し算と条件式）とを、慣習上区別している。

評価環境は以下のデータ型を使って定義される。

data EvalCont = Empty
              | Add1 EvalCont Aexp
              | Add2 EvalCont Int
              | IfZ0 EvalCont Aexp Aexp

対応する差し込み関数は以下の通りである。

plug :: (EvalCont, Aexp) -> Aexp
plug (Empty, ae)            = ae
plug (Add1 ec ae2, ae1)     = plug (ec, Comp (Add ae1 ae2))
plug (Add2 ec i1, ae2)      = plug (ec, Comp (Add (Val i1) ae2))
plug (IfZ0 ec ae1 ae2, ae0) = plug (ec, Comp (IfZ ae0 ae1 ae2))

計算は (1) リデックスと環境とに分解され、(2) リデックスが縮約され、(3) その結果が環境に差し込まれる、という簡約のステップを経る。

reduce1 :: (Comp, EvalCont) -> Aexp
reduce1 (Add (Val i1) (Val i2), ec) = plug (ec, Val (i1+i2))
reduce1 (Add (Val i1) (Comp s2), ec) = reduce1 (e2, Add2 ec i1)
reduce1 (IfZ (Val 0) ae1 ae2, ec) = plug (ec, ae1)
reduce1 (IfZ (Val i) ae1 ae2, ec) = plug (ec, ae2)
reduce1 (IfZ (Comp s0) ae1 ae2, ec) = reduce1 (s0, IfZ0 ec ae1 ae2)

評価は、値が得られるまで繰り返し行われる簡約によって記述される。

eval :: Aexp -> Int
eval (Val i)  = i
eval (Comp s) = eval (reduce1 (s, Empty))

[§4.1.2](脱関数化を実用する 4#section4-1-2) の解釈器が脱関数化の出力と正確に対応しているということが分かる。plugはecの適用関数なのである。ゆえに脱関数化への対応する入力は以下の通りである。

reduce1 :: (Comp, Aexp -> Aexp) -> Aexp
reduce1 (Add (Val i1) (Val i2), ec) = ec (Val (i1+i2))
reduce1 (Add (Val i1) (Comp s2), ec)
    = reduce1 (s2, \ae2 -> ec (Comp (Add (Val i1) ae2)))
reduce1 (Add (Comp s1) ae2, ec)
    = reduce1 (s1, \ae1 -> ec (Comp (Add ae1 ae2)))
reduce1 (IfZ (Val 0) ae1 ae2, ec) = ec ae1
reduce1 (IfZ (Val i) ae1 ae2, ec) = ec ae2
reduce1 (IfZ (Comp s0) ae1 ae2, ec)
    = reduce1 (s0, \ae0 -> ec (Comp (IfZ ae0 ae1 ae2)))

eval :: Aexp -> Int
eval (Val i)  = i
eval (Comp s) = eval (reduce1 (s, \e -> e))

reduce1が継続渡しスタイルで書かれているということが分かるだろう。ゆえにこの継続は構文論の評価環境を表しているのだ。

[§4.1.3](脱関数化を実用する 4#section4-1-3) ではreduce1が継続をカノニカルに使っているので、直接的なスタイルに戻すことができる [[10](脱関数化を実用する 8#reference10),[14](脱関数化を実用する 8#reference14)]。結果は以下の通りである。

reduce1 :: Comp -> Aexp
reduce1 (Add (Val i1) (Val i2))  = Val (i1+i2)
reduce1 (Add (Val i1) (Comp s2)) = Comp (Add (Val i1) (reduce1 s2))
reduce1 (Add (Comp s1) ae2)      = Comp (Add (reduce1 s1) ae2)
reduce1 (IfZ (Val 0) ae1 ae2)    = ae1
reduce1 (IfZ (Val i) ae1 ae2)    = ae2
reduce1 (IfZ (Comp s0) ae1 ae2)  = Comp (IfZ (reduce1 s0) ae1 ae2)

結果として得られた直接的スタイルの解釈器は、評価環境を暗に評価している。

値渡しのラムダ計算の構文論とその実装を提示する。

値渡しのラムダ計算について考えていく。ラムダ式は値（識別子かラムダ抽象）と計算とのどちらかである。計算は常に適用である。

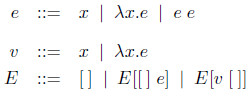
式 e の環境 E への差し込みは次のように定義される。

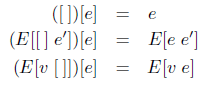
値（v₁, v₂, ...）の任意の適用は、すべてが何かに縮約するわけではないものの、リデックスと呼ばれる［redex は reducible expression の略である］。ベータリデックスだけが縮約し、他は行き詰まりとなっている。

そして簡約関係は次の規則によって定義される。

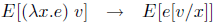
これらの定義は「一意分解」の補題を満たしているので、1ステップ簡約を関数として実装できる。

ラムダ計算は以下のデータ型を使って定義される。ここでは値と計算を区別している。

data Term = Val Value -- 些細な項
          | Comp Comp -- 重要な項

data Value = Var String
           | Lam String Term

data Comp = App Term Term

Termでは、些細な項、つまり値（変数とラムダ抽象）と、重要な項、つまり計算（適用）とを、慣習上区別している。

以下の型の置換関数も必要である。

subst :: (Term, Value, String) -> Term

評価環境は以下のデータ型を使って定義される。

data EvalCont = Empty
              | App1 EvalCont Term
              | App2 EvalCont Value

対応する差し込み関数は以下の通りである。

plug :: (EvalCont, Term) -> Term
plug (Empty, e)      = e
plug (App1 ec e', e) = plug (ec, Comp (App e e'))
plug (App2 x t, e)   = plug (x, Comp (App (Val t) e))

計算は (1) リデックスと環境に分解され、(2) 可能ならばリデックスが縮約され、(3) その結果が環境に差し込まれる、という簡約ステップを経る。ゆえに、(2) の可能性を説明するような選択型を使う。

reduce1 :: (Comp, EvalCont) -> Maybe Term
reduce1 (App (Val (Lam x e)) (Val t), ec)
    = Just (plug (ec, subst (e, t, x)))
reduce1 (s @ (App (Val (Var x)) (Val t)), ec)
    = Nothing
reduce1 (App (Val t) (Comp s), ec)
    = reduce1 (s, App2 ec t)
reduce1 (App (Comp s) e, ec)
    = reduce1 (s, App1 ec e)

またしても、何らかの値が得られるまで繰り返し実行する簡約を使って記述されている。選択型は行き詰まりの項を説明するために使う。

eval :: Term -> Maybe Value
eval (Val t) = Just t
eval (Comp s) = case reduce1 (s, Empty) of
    Just e  -> eval e
    Nothing -> Nothing

値を取得しない場合は2つある。行き詰まりの項を評価する場合と、発散する項を評価する場合（このときevalは停止しない）とである。

またしても、上述のプログラムが、plugがEvalContの適用関数であるような脱関数化の出力に対応しているということを私たちは見る。脱関数化の対応する入力は以下の通りである。

reduce1 :: (Comp, Term -> Maybe Term) -> Maybe Term
reduce1 (App (Val (Lam x e)) (Val t), ec)
    = ec (subst (e, t, x))
reduce1 (s @ (App (Val (Var x)) (Val t)), ec)
    = Nothing
reduce1 (App (Val t) (Comp s), ec)
    = reduce1 (s, \e -> ec (Comp (App (Val t) e)))
reduce1 (App (Comp s) e, ec)
    = reduce1 (s, \e' -> ec (Comp (App e' e)))

eval :: Term -> Maybe Value
eval (Val t)  = Just t
eval (Comp s) = case reduce1 (s, \e -> Just e) of
    Just e  -> eval e
    Nothing -> Nothing

reduce1はまたしても継続渡しスタイルで書かれているということが分かる。ゆえにその継続は構文論の評価環境を表しているのである。

reduce1は継続をカノニカルに使うので、行き詰まりの項に対してローカルな例外を使うことで、直接的なスタイルに戻すことができる。reduce1の直接的スタイルのバージョンは以下の通りである。［ここでは例外にMaybeモナドを使っている。］

reduce1 :: Comp -> Maybe Term
reduce1 (App (Val (Lam x s)) (Val t)) = do
    return $ subst (s, t, x)
reduce1 (s @ (App (Val (Var x)) (Val t))) = do
    Nothing
reduce1 (App (Val t) (Comp s)) = do
    t' <- reduce1 s
    return $ Comp (App (Val t) t')
reduce1 (App (Comp s) e) = do
    t' <- reduce1 s
    return $ Comp (App t' e)

eval :: Term -> Maybe Value
eval (Val t) = return t
eval (Comp s) = do
    t' <- reduce1 s
    eval t'

結果として得られたのは、算術式のときと同様、評価環境を暗に表している直接的スタイルの解釈器である。

これまで、2つの構文論に対する解釈器を考え、評価環境と差し込み関数が継続を脱関数化したものに相当するということを見た。この観察により、私たちは両方の解釈器を直接的なスタイルで実装するに至った。（この意味で、[§3](脱関数化を実用する 3#section3) と [§4](脱関数化を実用する 4#section4) は対照的である。というのも [§3](脱関数化を実用する 3#section3) は直接的なスタイルのプログラムから始まり、脱関数化されたCPSのプログラムで終わっているからである。）この観察はさらに、評価環境の文法を言語のBNFから自動的に得る方法も示している。BNFに対する再帰下降（1ステップ簡約関数など）をCPSにしたものにあたるものを脱関数化するのである。継続を表すこのデータ型は望まれた文法と同型であり、適用関数は対応する差し込み関数となっている。

一般に、評価環境は、評価が基本的な環境を使って左か右に簡単に拡張できるように記述されている。値渡しのλ計算については、2つの仕様は次のように得られる。

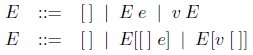
あるいは明示的な合成演算子 ∘（(E₁ ∘ E₂)[e] = E₁[E₂[e]]）を使って書けば、

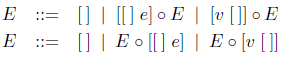
評価環境は全て基本的な環境を使って構成され、かつ合成は結合的であるので、2つの使用は実質的に同じ環境を定義している。表し方だけが違っているのである。1番目の表し方では、評価環境は基本的な環境のリストと同型である。2番目の表し方では、同じ評価環境が反転されたリストと同型である。

ゆえに、1番目の表し方では、式の環境への差し込みは環境に対する右折り畳みによって再帰的に行われ［註：foldr f b [x1, x2, ..., xn] = f x1 (f x2 (...(f xn b)...))］、2番目の表し方では、式の環境への差し込みは環境に対する左折り畳みによって反復的に行われる［註：foldl f b [xn, ..., x2, x1] = f (f (...(f b xn)...) x2) x1］。後者は§4.1.2と§4.2.2において暗に行ってきたことである。それを踏まえて、言語のBNFからどのように評価環境の文法を取得できるかについての上述の観察について再考察しよう。結果として得られる文法が2番目の種類のものであり、関連する差し込み/適用関数が（左畳み込みと同様に）反復的であるということが分かる。

算術式と値呼びラムダ計算を表す最初の方法に戻ろう。算術式に対するまだ述べていないBNFは以下の通りである。

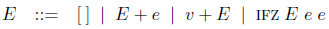
2つの解釈器では、分解が評価環境を作り出し、差し込みがそれを消費する。合成と差し込みの子の差し込みを森林伐採すると、[§4.1.4](脱関数化を実用する 4#section4-1-4) と [§4.2.4](脱関数化を実用する 4#section4-2-4) で得たものと同じ直接的スタイルの解釈器が得られる、ということが分かる。

構文論の評価環境の表し方の種類（例えばあるいはデータ型として、あるいは関数として）によって、プログラムについての推論にどういう影響があるのか、興味を持っているかもしれない。次のセクションでは、プログラムの正当性証明が脱関数化の前後でどう変わるのかを調べる。