Иллюстрация - sergeresko/Lem_in-explanation GitHub Wiki
Вот иллюстрация работы алгоритма Бхандари на примере, которым я пользовался в процессе написания своего Lem_in: https://github.com/sergeresko/lem_in/blob/master/_maps/3-groups.map.
На фотографии ниже изображён процесс нахождения путей, я на неё буду ссылаться. Нумерация рисунков:
A1 A3 A5
A2 A4
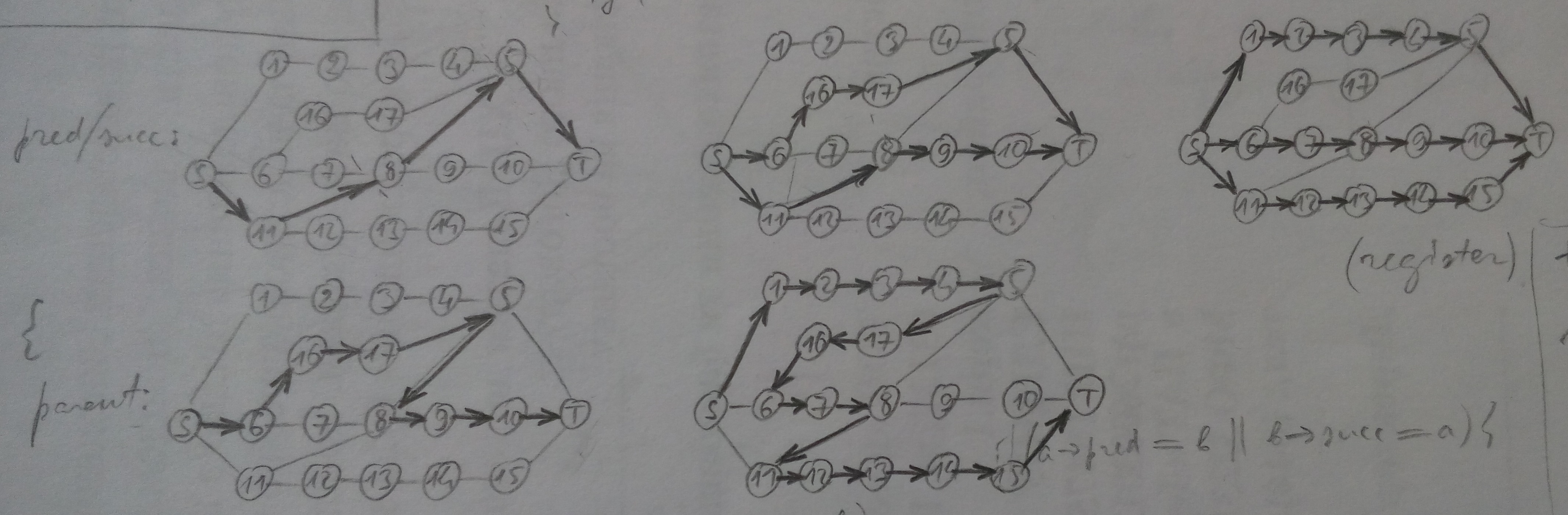
Первый запуск алгоритма
Рис. R1 — Граф выглядит так. Стрелки, которые выходят из комнаты, обозначают рёбра, хранящиеся в списке links этой комнаты (если вес ребра не указан на рисунке, он равен 1).
1) modify graph: не делает ничего, т.к. все pred/succ равны NULL
2) find path: в результате работы алгоритма Дейкстры мы получим путь S-11-8-5-T, который будет представлен так:
room | S | 11 | 8 | 5 | T
--------+------+----+----+---+---
parent | NULL | S | 11 | 8 | 5
На рис. R1 около вершин подписаны их distance и parent.
3) adjust parents: ничего не делает
4) restore graph: ничего не делает
5) combine paths: поскольку в pred/succ пока ничего нет, просто сохраняем в них найденный путь:
room | S | 11 | 8 | 5 | T
------+------+----+----+---+------
pred | NULL | S | 11 | 8 | NULL
succ | NULL | 8 | 5 | T | NULL
Этот путь показан на рис. A1.
Второй запуск алгоритма
1) modify graph: делим вершины вдоль пути, который хранится в pred/succ:
Рис. R2
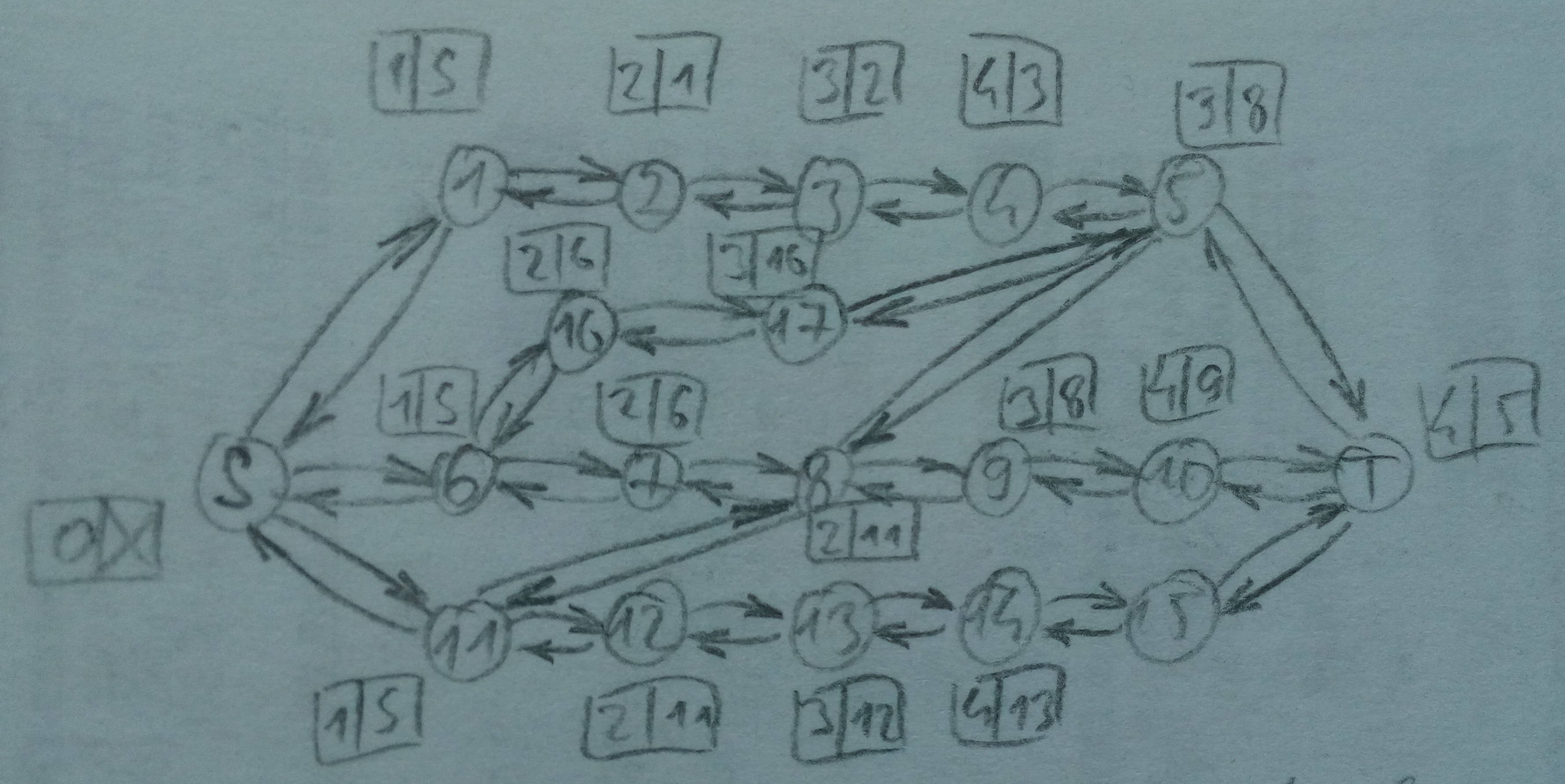
2) find path: алгоритм Дейкстры найдёт путь S-6-16-17-5in-8out-9-10-T, который будет представлен через parent (рис. R2).
3) adjust parents: зависит от реализации; идея в том, чтобы после выполнения следующего (4-го) шага через parent оказался представленным путь S-6-16-17-5-8-9-10-T.
4) restore graph: склеиваем вершины вдоль пути, который хранится в pred/succ: связи через links вновь приобретают такой вид, как на рис. A1, а поля parent имеют такие значения (рис. A2):
room | S | 6 | 16 | 17 | 5 | 8 | 9 | 10 | T
--------+------+---+----+----+----+---+---+----+----
parent | NULL | S | 6 | 16 | 17 | 5 | 8 | 9 | 10
5) combine paths: совмещаем этот путь с тем, что хранится в pred/succ, убирая накладывающиеся участки (в данном случае участок 5-8 есть в обоих путях), получим:
room | S | 6 | 16 | 17 | 5 | 11 | 8 | 9 | 10 | T
------+------+----+----+----+----+----+----+----+----+------
pred | NULL | S | 6 | 16 | 17 | S | 11 | 8 | 9 | NULL
succ | NULL | 16 | 17 | 5 | T | 8 | 9 | 10 | T | NULL
Это соответствует двум путям, которые изображены на рис. A3.
Третий запуск алгоритма
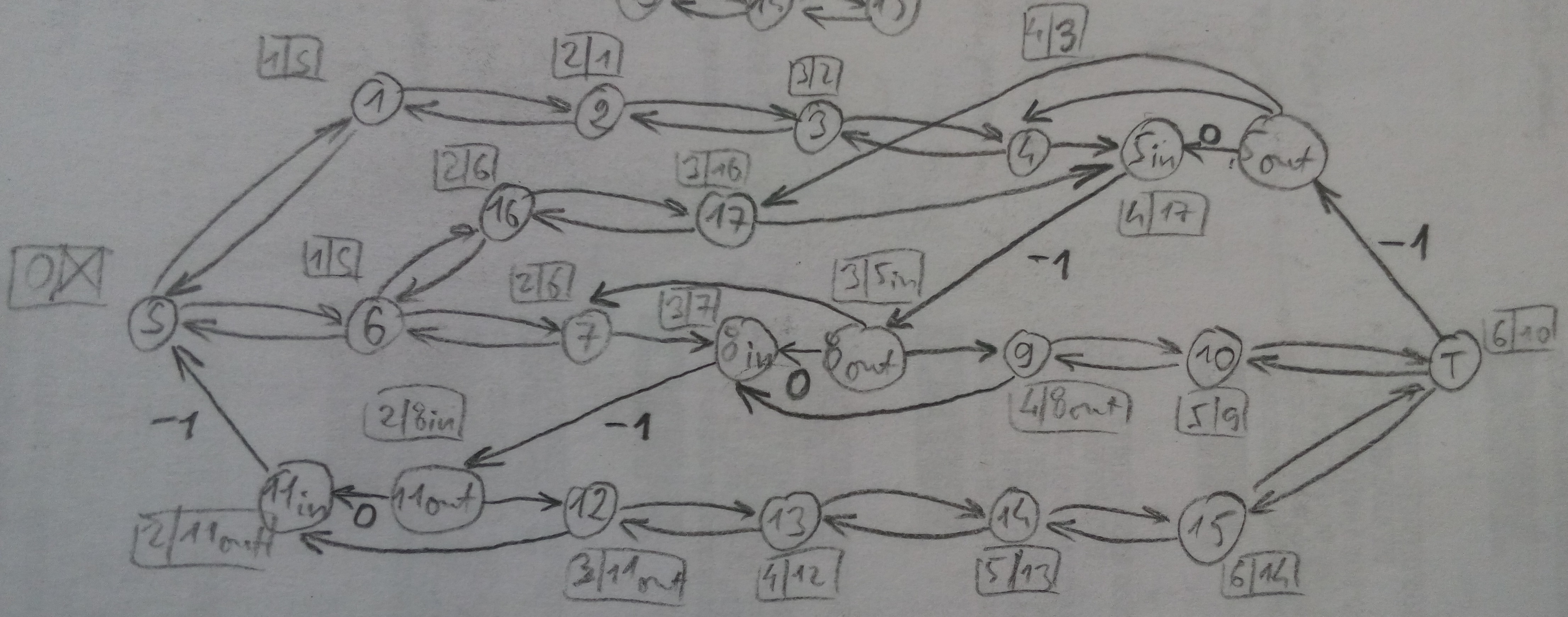
1) modify graph: делим вершины вдоль обоих путей, которые хранится в pred/succ:
Рис. R3 (На рисунке ошибка: стрелка из 5out должна идти не в 8out, а в 8in.)
2) find path: алгоритм Дейкстры найдёт путь S-1-2-3-4-5in-17out-17in-16out-16in-6out-7-8in-11out-12-13-14-15-T (рис. R3)
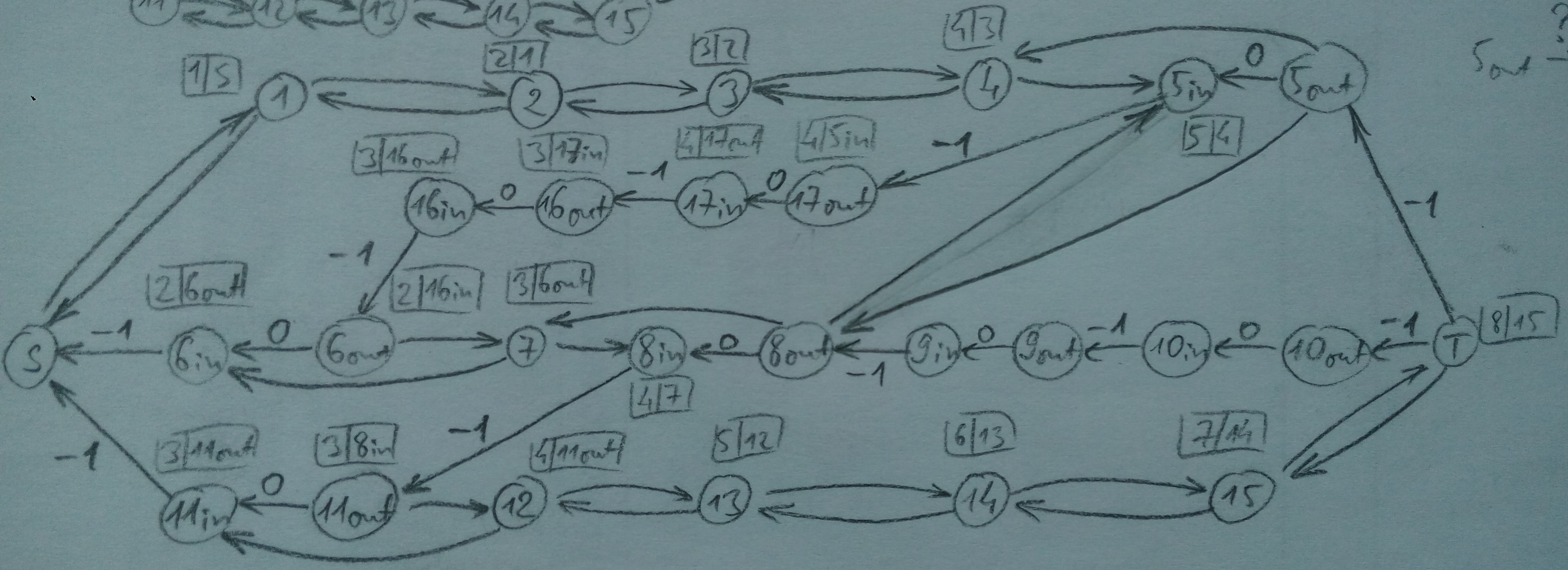
3) adjust parents: меняем поля parent так, чтобы после выполнения следующего шага они указывали путь S-1-2-3-4-5-17-16-6-7-8-11-12-13-14-15-T (рис. A4)
4) restore graph: склеиваем вершины вдоль обоих путей, которые хранится в pred/succ
5) combine paths: совмещаем новый путь (рис. A4) с теми двумя (рис. A3), устраняя наложения (участки 6-16-17-5 и 17-8)
room | S | 1 | 2 | 3 | 4 | 5 | 17 | 16
------+------+---+---+---+---+---+------+------
pred | NULL | S | 1 | 2 | 3 | 4 | NULL | NULL
succ | NULL | 2 | 3 | 4 | 5 | T | NULL | NULL
room | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | T
------+---+---+---+----+----+----+----+----+----+----+------
pred | S | 6 | 7 | 8 | 9 | S | 11 | 12 | 13 | 14 | NULL
succ | 7 | 8 | 9 | 10 | T | 12 | 13 | 14 | 15 | T | NULL
Получили три пути, изображённые на рис. A5.
Дальше: Алгоритм Дейкстры