Tema #6 Estructura de datos generales - sebas-mora28/Algoritmos_Estructuras_Datos_I GitHub Wiki

• Los grafos son estructuras de datos generales aplicables en muchas áreas como:

      * Sociología 
      * Química
      * Geografía 
      * Criminología 
  

• Un grafo G agrupa entidades que representan conceptos.

• Se compone de vértices/nodos que representan cada entidad y de aristas/arcos que representan relacionados entre los nodos.

• Un grupo puede ser dirigido o no dirigido. El ejemplo anterior es un grafo no dirigido. El siguiente es un grafo dirigido.

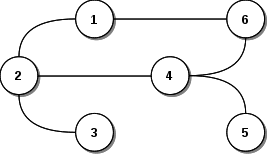
• Los arcos pueden tener magnitud, creando un grafo con peso:

• El grado de un nodo es la cantidad de conexiones en las que participa. Por ejemplo:

  • Cartago = 5

• En un grafo dirigido hay grafo saliente y entrante.

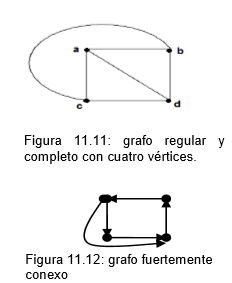
• Un camino P={V, V1, V2,..., Vn} es el conjunto de vértices que conectan V0-->Vn

• Un ciclo es un camino que empieza y termina en el mismo nodo.

• Un grafo es acíclico si no tiene ciclos.

• Un DAG(Directed Acyclic Graph) es un nodo dirigido sin ciclos

¿ Cómo se implementar un grafo?

• Hay dos formas:

       * Matriz de la adyacente
       * Lista de adyacentes
  

Matriz de adyacencia

• Dadi un grafo de n vértices, se constituye una matriz de nxn donde cada elemento a(i,j) tiene uno de los siguientes valores:

   * 1 si hay arco de Vi-Vj
   * 0 en caso contario 
  

• Una lista de adyacencia es una lista enlazada donde cada elemento es un nodo de grafos. Cada elemento tiene una lista con sus conexiones

• Si el grafo tuviera pesos en vez de 1 se pondrá el peso y en vez de 0, se pondrá infinito.

• Una lista de adyacencia es una lista enlazada donde cada elemento es un nodo de grafos. Cada elemento tiene una lista con sus conexiones.

• Elegir entre uno y otra forma depende de:

        - Algoritmos por aplicar
        - Densidad del grafo
        - ALTA-Matriz
        - BAJA-lista
  

¿ Cómo se implementar un grafo?

• Se recorre desde un nodo específico y hasta recorrer todos los nodos alcanzable.

• Recorrido por archura: (FiFo)

• Por profundidad: (LiFo

La ruta más corta entre un nodo y otro

• Es uno de los problemas más comunes de los grafos

• Edgar Dijskta propone un algoritmo que calcula la ruta más corta.

                    * Grafo por peso
                    * Grafo dirigido 
  

Pasos

• Asignar a todos los nodos infinito menos al inicial

• Calcular el valor a todos los nodos a partir de A.

• Selecciona el nodo menor y nos movemos a este. Se recalcula las distancias usando el nuevo nodo como "puente".

• Se sigue seleccionando el menor no visitado y se recalcula.

Algoritmo de Washall ( Cierre transitivo)

• Permite determinar si hay camino entre cualquier par de nodos del grafo.

• Calcule la matriz de caminos de un grafo G de n vértices representando la matriz de adyacencia A

• Define una secuencia de matrices Po, P1,...,Pn. Los elementos de cada matriz Pk[i,j] tienen un cero si no hay camino, o 1 si hay camino de Vi a V, através de Vk.

P0	1	2	3	4	5
1	1	1	0	0	0
2	0	1	0	1	1
3	1	1	1	0	1
4	1	0	0	1	1
5	0	0	0	1	1

• A partir de la matriz Pk-1

P1	1	2	3	4	5
1	1	1	0	0	0
2	0	1	0	1	1
3	1	1	1	0	1
4	1	1	0	1	1
5	0	0	0	1	1

* Hay camino de V4 a V2 a través de V1

P2	1	2	3	4	5
1	1	1	0	1	1
2	0	1	0	1	1
3	1	1	1	1	1
4	1	1	0	1	1
5	0	0	0	1	1

* Así sucesivamente hasta llegar a P5

Algoritmo de camino más corto para todos los vértices

• Se podría aplicarDijkstra para todos los vértices pero sería ineficiente.

• El agoritmo de FLoyd-Washall es más directo para calcular los rutas óptimas para todos los vértices.

• El grafo se representa con la matriz de pesos. Si no hay arco/ arista se conserva infinito.

• La diagonal es infinito.

• Al igual que Warshall, genera n matrices de nxn. En cada paso, se incorpora un nuevo vértice y se evalúa a ratos.

• De igual forma, se generan n matrices predecesoras.

     Wo[i,j]   ----> Cij peso del arco de V1 A v
                ----> inf si no hay arco 
  

W1[i,j] = mínimo ( D0[i,j], D0[i,1], D0[1 ,j])

WK[i,j] = min ( Dk-1[i,j], Dk-1[i,k] + Dk-1[k,j])