• Un árbol es una estructa de datos jerárquica, es decir, la forma en la que se conectan los elementos permite identificar niveles de importancia.

• Los árboles se componene de nodos. Cada nodo contiene un dato y una o más referencias a otros nodos.

• En un árbol binario, cada nodo tiene a lo sumo dos nodos.

• Existen árboles binarios N-arios, en los que los nodos pueden tener más de dos nodos.

• Estructura básica de un árbol binario:

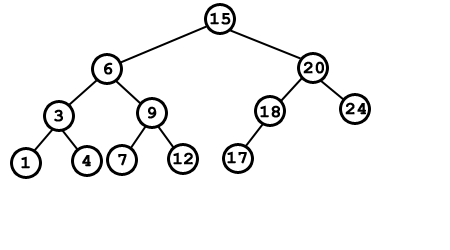
¿Cómo se define un nodo en Java?

class Nodo {
    int element;
    Nodo right; 
    Nodo left; 
}

¿Cómo se define el árbol?

class BST {
    Nodo root = null;
    
    boolean isEmpty(){
      return root == null;
    }
}

¿Cómo se busca en el árbol?

boolean contains(int e){
     return this.contains(e, root);
}

private boolean contains(int element; Nodo current){
    if(current == null){
         return false;
    } else if (element < current.element){
         return contains(e, current.left);
    }else if(element > current.right){
         return constains(e, current.right);
    }else{
       return true;
    }
}

¿Cómo se elimina un elemento en el árbol?

Hay tres posibles escenarios:

• Si el nodo que se elimina es un hijo:

     - En este caso simplemente se "rota" la referencia. * Si el nodo por eliminar tiene un solo hijo 
    
     - En este caso, se salta el nodo por eliminar y su hijo lo remplaza
  

• Si el nodo por eliminar tiene dos hijos. En este caso:

      - 1. Se busca el elemento menor en el subárbol derecho o el mayor en el subárbol izquierdo.
    
      - 2.  Se copia el elemento encontrado en 1 el nodo por eliminar.
  
      - 3. Se ejecuta el proceso de eliminación a partir de la posición en la que se copió el elemento encontrado en 1. 
  

private Nodo remove(int e; Nodo c){
    if(nodo == null){
          return null;
    }
    if (e < c.value){
         c. left = remove(e, c.left);
    }
    else if(e > c.value){
        c.right = remove(e, c.right);
    }
    else if(c.left != null && c.right != null){
        c.value = findmin(c.right).value;
        c = c.right = remove(c.value. c.right);
    }else{
        c. left != null ? c.left : c.right;
    }
    return c;
}

Árboles AVL

• Uno de los supuestos de los árboles es que proveen búsquedas rápidas.

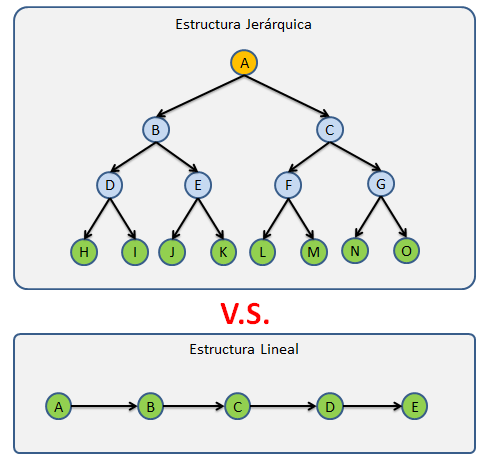
• Dependiendo del orden de inserción se puede obtener un árbol como el de la izquierda:

• ¿Qué sucede en este caso?

    * Se pierde la rapidez para buscar y se reduce a una búsqueda secuencial
  

• AVL significa Adelson-Velskii-Landis

• Es un árbol binario de búsqueda con una combinación de balance para asegurar que la búsqueda sea óptima.

• La altura a la izquierda no puede diferir en más de 1 con respecto a a la derecha.

• Niveles de un árbol

• La altura de un árbol es el nivel máximo + 1.

• Cada nodo tiene el factor de balance como atributo.

¿Cómo se inserta en un AVL?

• Igual que en un BTS
• Puede resultar en una violación de balance
• En caso de violación. se aplica una rotación
• Hay varios casos
• El balance en cada nodo no puede difererir en -1,0,1

Árboles B

• Son árboles n-arios (Pueden tener más de dos hijos)

• Optimización para estar almacenados en el disco. Los árboles vistos hasta el momento asumen que están en memoria completamente.

    * No es factible si hay muchos datos 
  

• El problema de tener una estructura en disco es la latencia asociada a estos.

• Los discos son sumamente lentos en comparación a la memoria principal.

• Los B-trees están optimizados para no tener tantas operaciones en el disco.

• Un B-tree gráficamente

• Los B-trees reducen la profundidad del árbol

• Siempre está balanceado

• Los nodos se llaman páginas

• A exepción de la raíz, los nodos siempre están medios llenos.

• B-tree de orden tiene las siguinetes características:

  * Todas las hojas están en el mismo nivel 
  
  * Todos los nodos tienen a lo sumo m ramas ( y m-1 llaves)
  
  * Como mínimo cada nodo(excepto la raíz)  tiene al menos m/2 ramas.
  

Árboles de expresión

• Una expresión es una secuencia de "tokens" (componentes léxicos que siguen una estructura específica) * Operadores, palabras claves

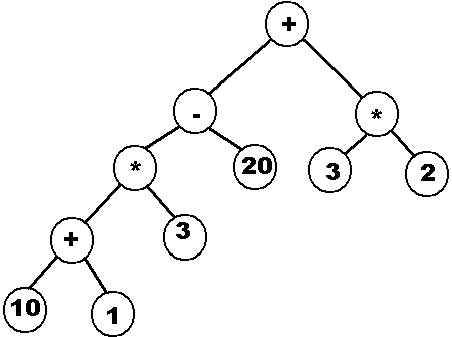
• Un árbol de expresión es un árbol binario con las siguientes propiedades:

      * Cada hoja es un operando 
      * Cada raíz son operadores
      * Cada subárbol es una expresión
  

• Los compiladores usan árboles de expresión extensamente

• Para convertir el árbol a expresión, simplemente se debe recorrer el árbol con algunas de las siguientes formas:

       * Infijo (hizo izquierdo, raíz, hijo deerecho)
       * Postfijo (izquierdo, derecha, raíz)
       * Pre-fijo (raíz, izquierdo, derecho)
  

infijo(nodo){
     if(nodo != null){
         if(nodo==operador){
                 print("(");
         }
         infijo(nodo.izq);
         print(nodo.value);
         infijo(nodo.derecho);
         if(nodo == operador){
          print(")");
        }
     }