Algoritmos de Ordenamiento

• Mantener listas de elemento ordenados es importante para facilitar las bísquedas.

• Una lista de elementos desordenados no permite realizar búsquedas de manera eficiente.

• Hay muchos algoritmos de ordenamiento.

• La meta es encontrar algoritmos cada vez efecientes.

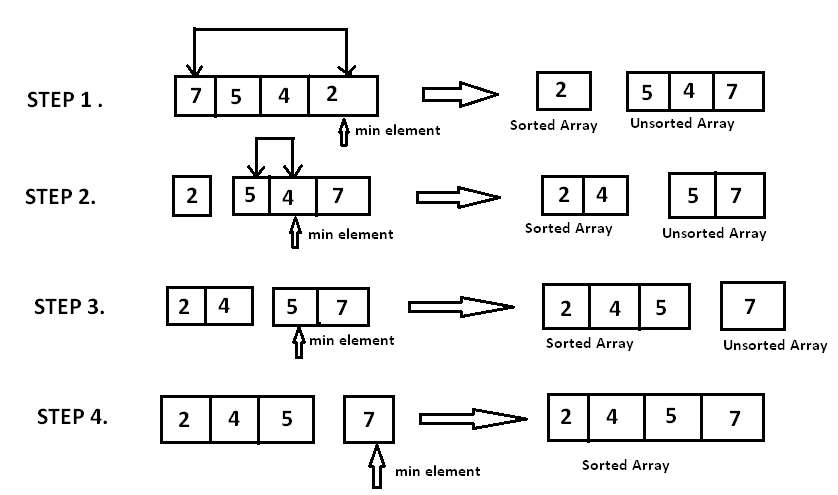
Selection Sort

• Consiste en buscar el menor elemento, sacarlo de una lista, ponerlo en otra y repetir hasta que la lista original esté vacía.

• Este enfoque es costoso en términos de espacio

• Se puede mejorar:

static void selecSort(){
    int end = size -1;
    for(int current =0; current < end; current++){
        swap(current, minimo(current, end));
    }
}

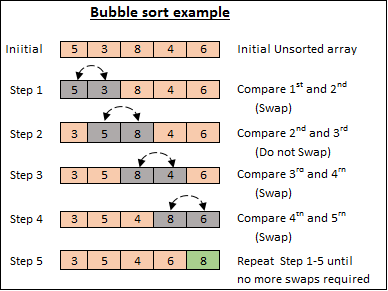
Bubble sort

• Consiste en "empujar" el mayor hacia el final de la lista.

• Únicamente se componen elementos adyacentes.

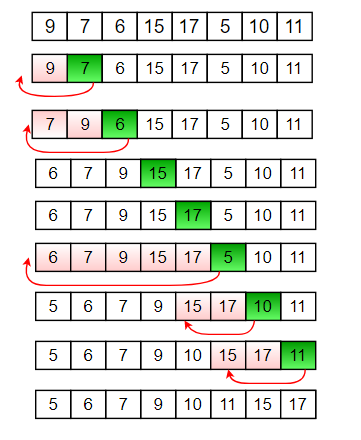
Insertion Sort

• La lista se divide en dos partes:

       * Elementos ordenados 
       * Elementos desordenados 
  

• No existen dos listas aparte, es lógica.

• Al insertar en la lista ordenada, se va corriendo los elementos hasta encontrar la posición que le corresponde al elementos por insertar.

public class InsertionSort { 
    
     public void insertionSort(int[] A){
          int in=0;
          int out=0;
          for(out =1; out < A.length; out++){
             int temp = A[out];
             in = out;
             while( in > 0; && A[in-1] <= temp){
                  A[in] = A[in-1];
                  --in;
             }
             A[in] = temp;
          }
     }
}

MergeSort

* Parte el array en dos.
* Llama recursivamente en cada mitad.
* Cuando la recursión llega a array de un elemento, se devuelve y empieza a unir en orden cada subarray.

QuickSort

• El más popular de los algoritmos de ordenamiento.

      * El más rápido en la mayoría de clases
      * Particiona el arreglo en dos y se llaman recursivamente en cada mitad.
  

• El paso inicial es calcular el pivote. El pivote es el elemento central del arreglo.

• Internamente compara los elementos previos y posteriores al pivote contra el valor del pivote.

• Hace swap a los elementos para colocarlos en la mitad que le corresponde.

• Cuando los indeces se cruzan, se recorre en cada mitad

Radix Sort

• Utiliza un enfoque distinto al resto de algoritmos de ordenamiento vistos hasta el momento.

• Los algoritmos vistos consideran la llave (el elemento de la lista) como una unidad indivisible.

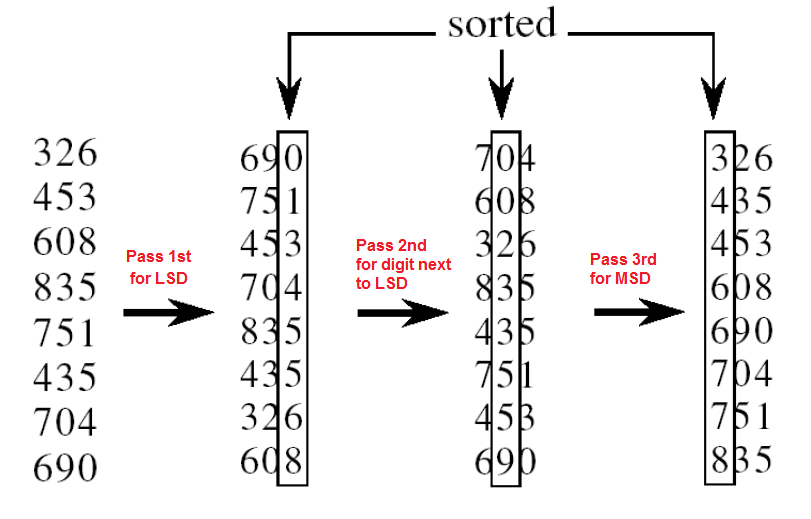
  * Por ejemplo, el 100 se considera 100 se constituye como el número 100
  * Sin embargo, Radix Sort divide la llave en cada uno de sus dígitos y ordena ṕara cada uno de estos. 
  

• Radix = Base/raíz del sistema numérico.

  * Si se ordena números de base 10, radix = 10;
  * Si se ordena número de base 2, radix = 2;
  

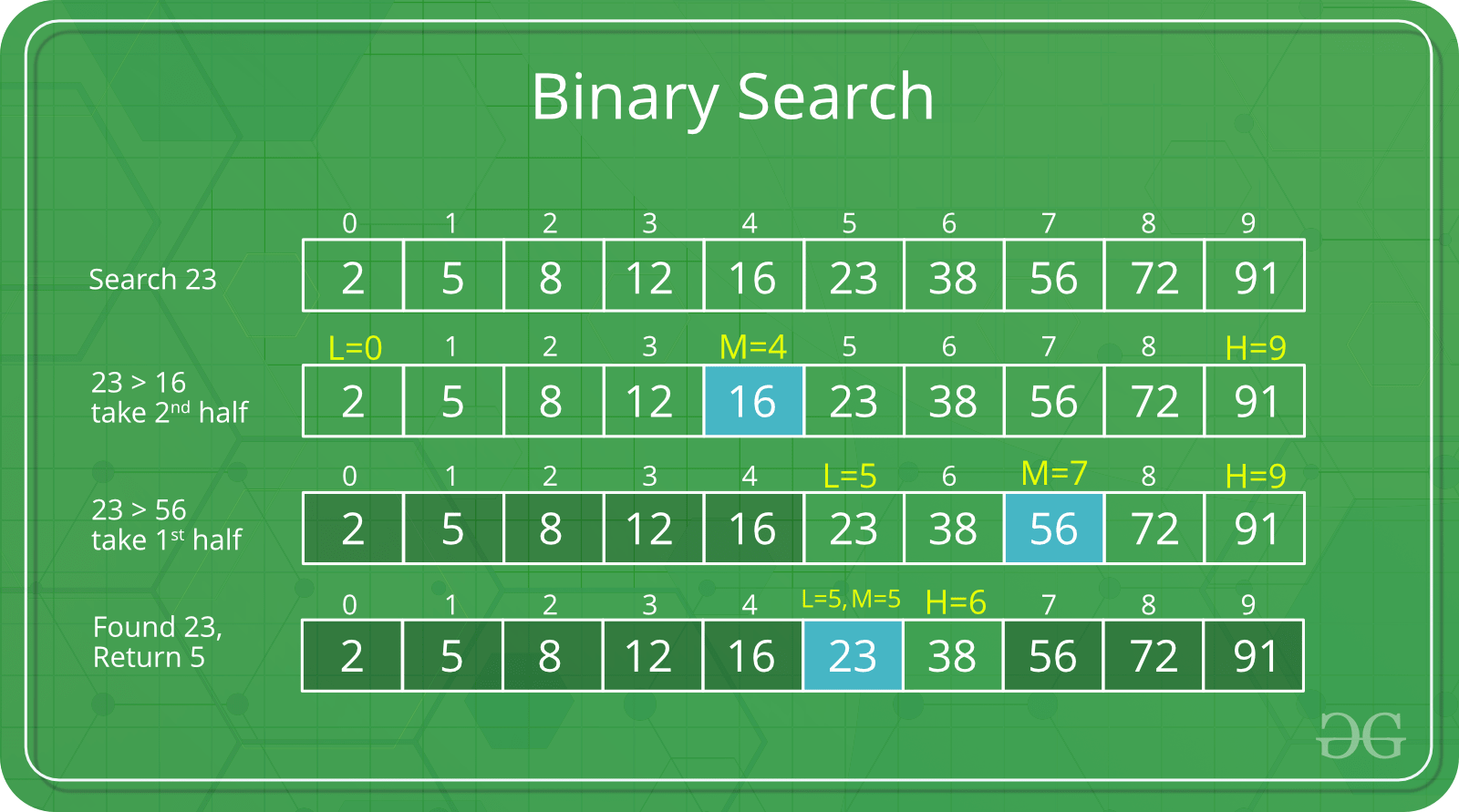
Binary Search

• Buscan un elemento en una lista/ array ordenado

• Compara el elemento central del array contra el elemento buscado.

• Si el central == buscado, termina.

• Si no:

  • Central > buscado, se busca en la mitad inferior

  • Central < buscado, se busca en la mitad superior