Introduction

Quick sort 1(https://en.wikipedia.org/wiki/Quicksort) is another classical divide-and-conquer algorithm for sorting, which was developed by the British computer scientist Tony Hoare in 1959. When implemented well, quick sort algorithm can be two or three times faster than its predecessors and competitors such as merge sort, which is why it gains its name.

Algorithm

Intuition

Given a list of values to sort, the quick sort algorithm works in the following steps:

1. Partitioning: First, it selects a pivot value to divide the list into two sub-lists.
   • a sub-list of the values < pivot value,
   • a sub-list of the values >= pivot value.

This process is also called partitioning. The strategy of choosing a pivot value can vary. One can choose the first element in the list as the pivot, or randomly pick an element from the list.

2. After the partitioning process, the original list is then reduced into two smaller sub-lists which are then recursively sorted.

3. After the partitioning process, we are sure that all elements in one sub-list are less or equal than any element in another sub-list. Therefore, we can simply concatenate the two sorted sub-lists that we obtain in step [2] to obtain the final sorted list.

The base cases of the recursion in step [2] are either when the input list is empty or contains only a single element. In either case, the input list can be considered as sorted already.

Th essential idea of quick sort is the partitioning process, which reduces the problems into smaller scale and meanwhile moves towards the final solution, i.e. after each partitioning, the overall values become more ordered.

Algorithm

public class Solution {
    public void quickSort (int [] lst) {
        // Sorts an array in the ascending order in O(n log n) time
        int n = lst.length;
        qSort (lst, 0, n - 1);
    }

    private void qSort (int [] lst, int lo, int hi) {
        if (lo < hi) {
            int p = partition (lst, lo, hi);
            qSort (lst, lo, p - 1);
            qSort (lst, p + 1, hi);
        }
    }

    private int partition(int [] lst, int lo, int hi) {
        // Picks the last element hi as a pivot and returns the index of pivot value in the sorted array
        int pivot = lst[hi];
        int i = lo;
        for (int j = lo; j < hi; ++j) {
            if (lst[j] < pivot) {
                swap(lst, i++, j);
            }
        }
        swap(lst, i, hi);
        return i;
    }
    
    void swap(int[] lst, int i, int j) {
        int tmp = lst[i];
        lst[i] = lst[j];   
        lst[j] = tmp;
    }
}

Complexity

• Depending on the pivot values, complexity can value from best/average O(NlogN) to worst O($N^2$).
• In the best case, the pivot is the median of the list => results in a BST => height of BST is logN and we need to scan each level once O(N) => O(NlogN)
• In the worst case the pivot is either the smaller or biggest element in the list, we end up with one partition with only one element, we have to execute this N times and each time scan N elements.

Example:

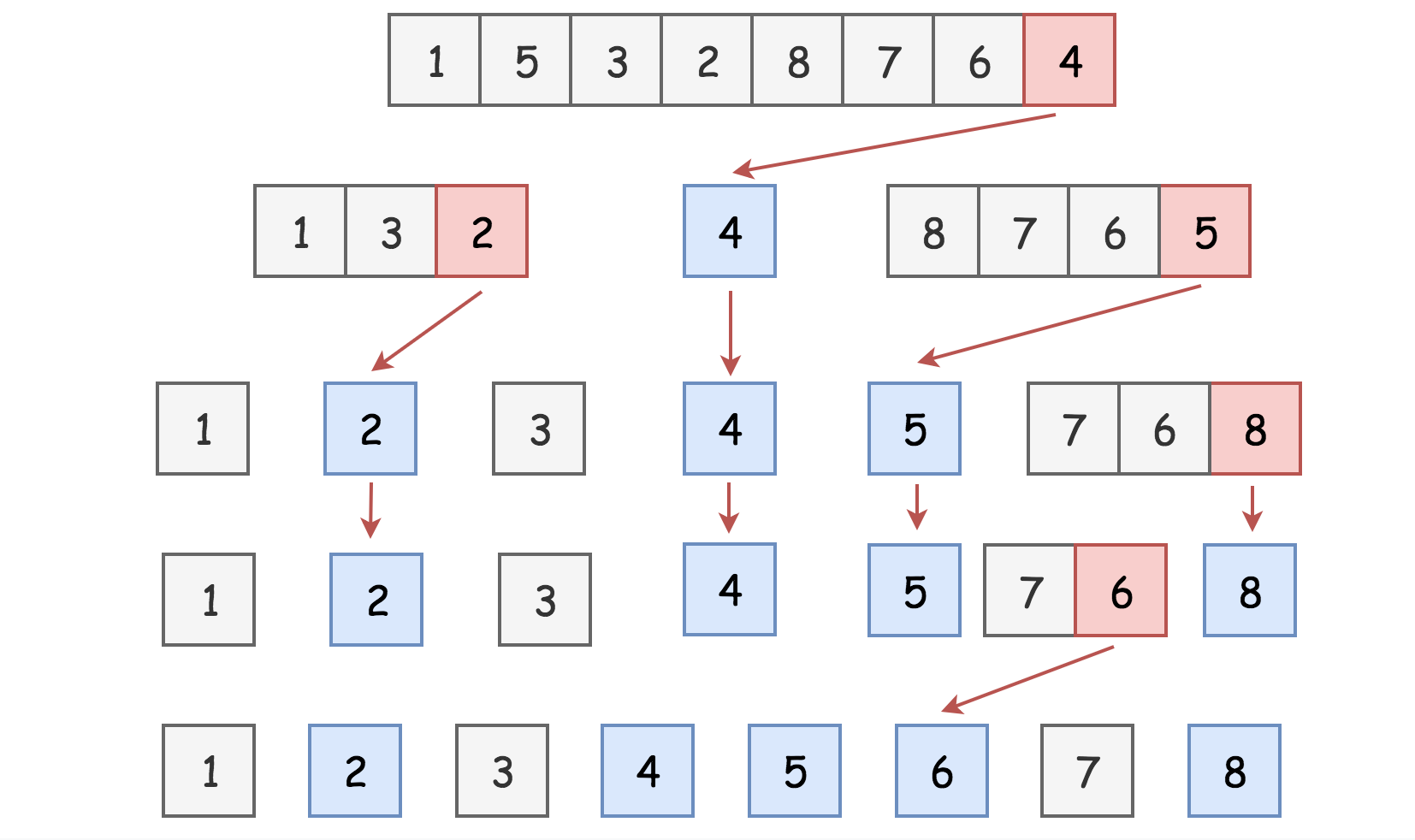
• First pivot 4
• Recursively sort resulting sublists
• Concatenate results