Merge Sort

A classic examples of the divide-and-conquer algorithm.

The merge sort algorithm can be divided into three steps, like all divide-and-conquer algorithms:

1. Divide the given unsorted list into several sublists. (Divide)
2. Sort each of the sublists recursively. (Conquer)
3. Merge the sorted sublists to produce new sorted list. (Combine)

Top-down approach

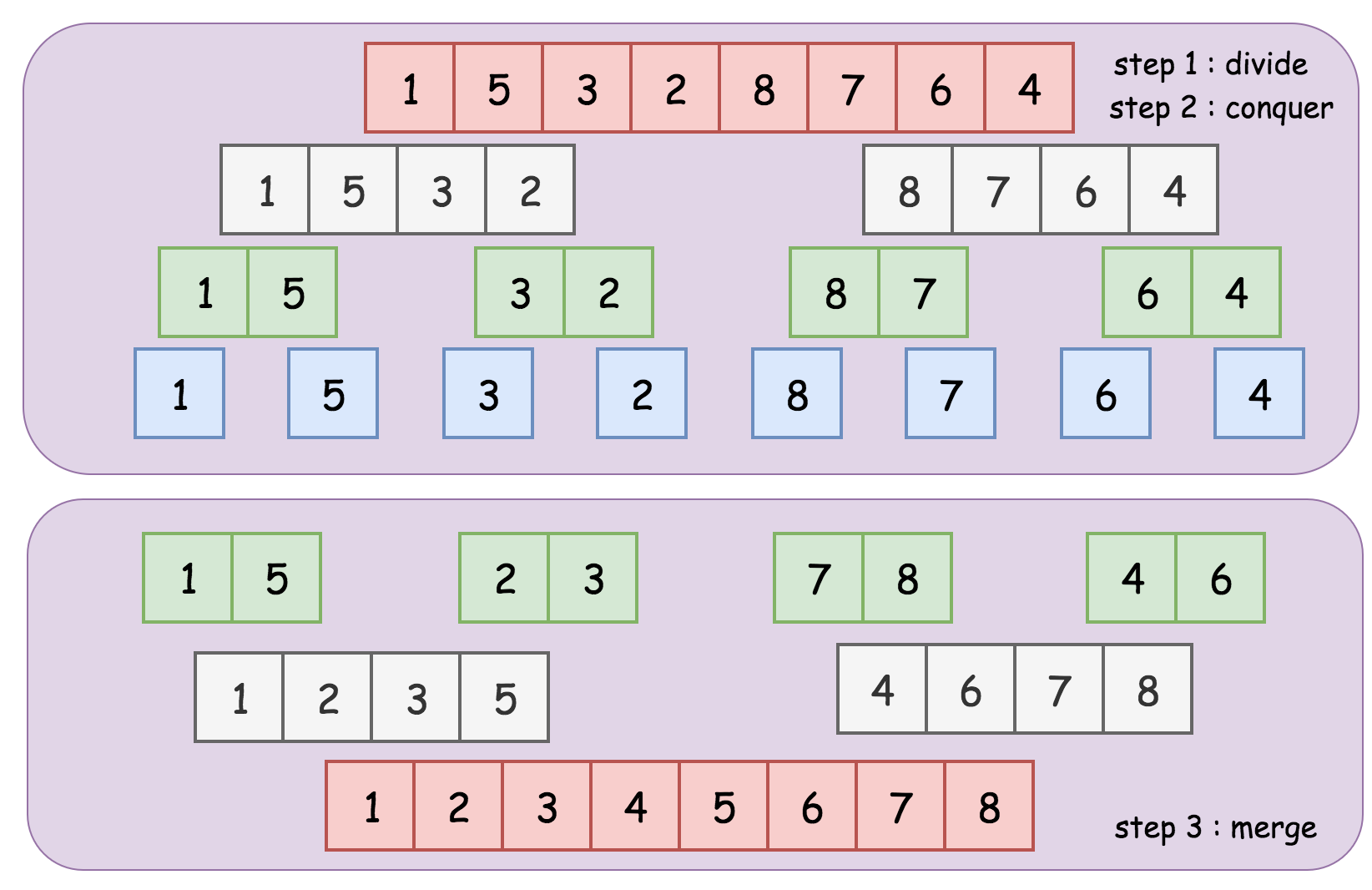
In the first step, we divide the list into two sublists, then we recursively sort the sublist in the previous step. Finally we merge the sorted sublists in the above step repeatedly to obtain the final list of sorted elements.

The recursion would reach the base case where the input list is either empty or contains a single element.

Merging two sorted lists can be done in linear time complexity O(N) where N is the total lengths of the two lists to merge.

• Algorithm

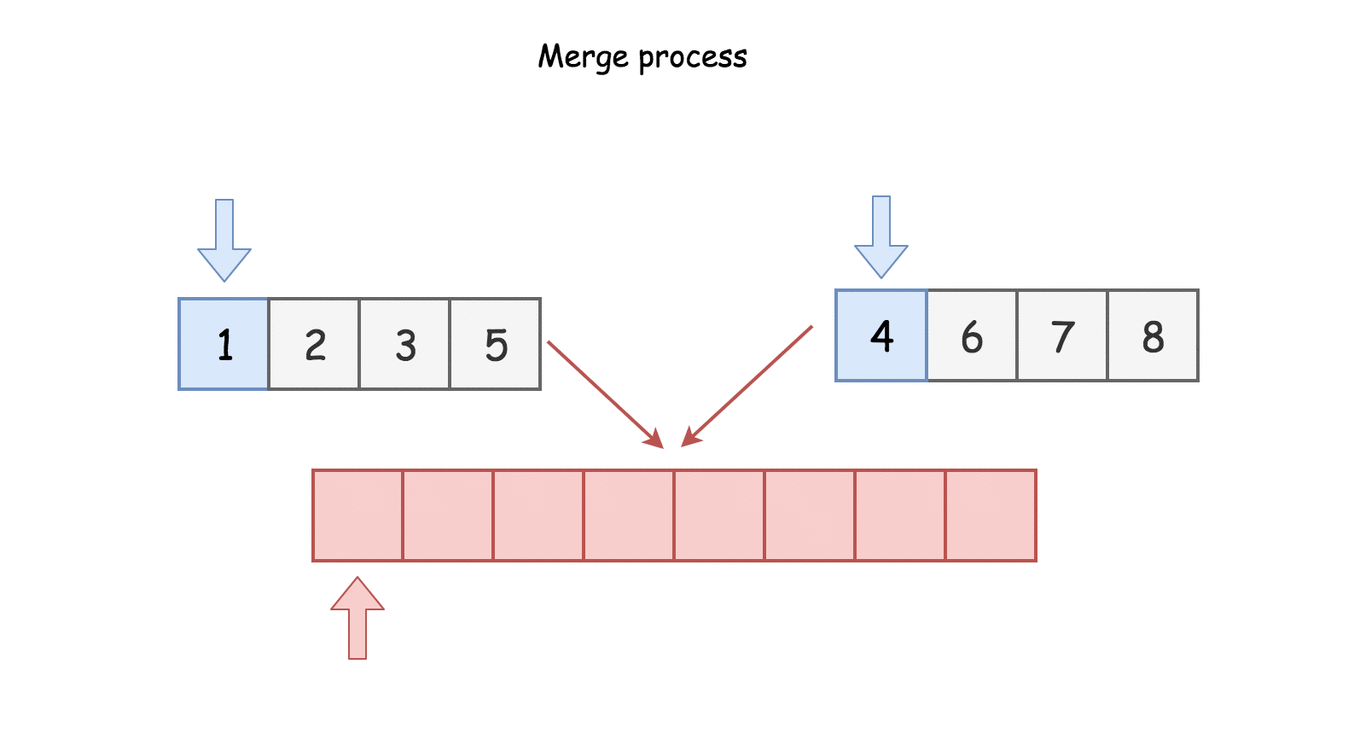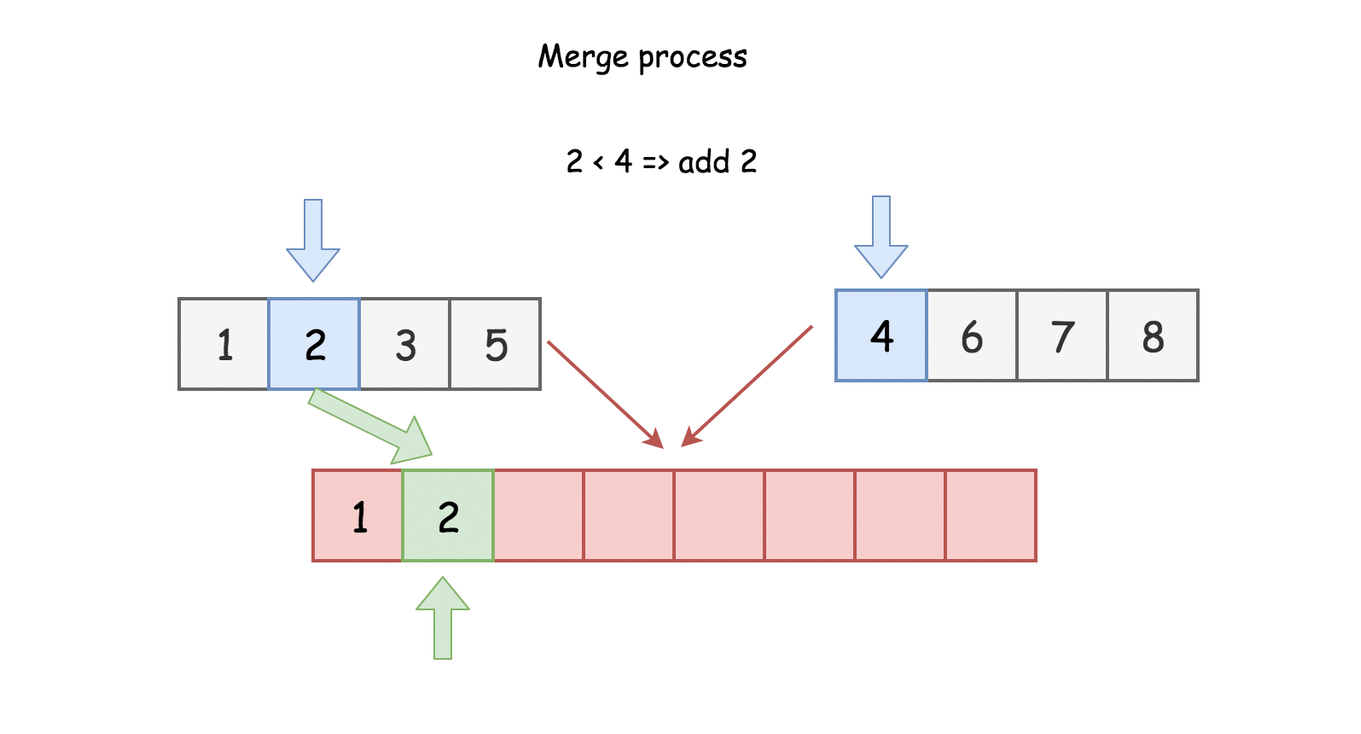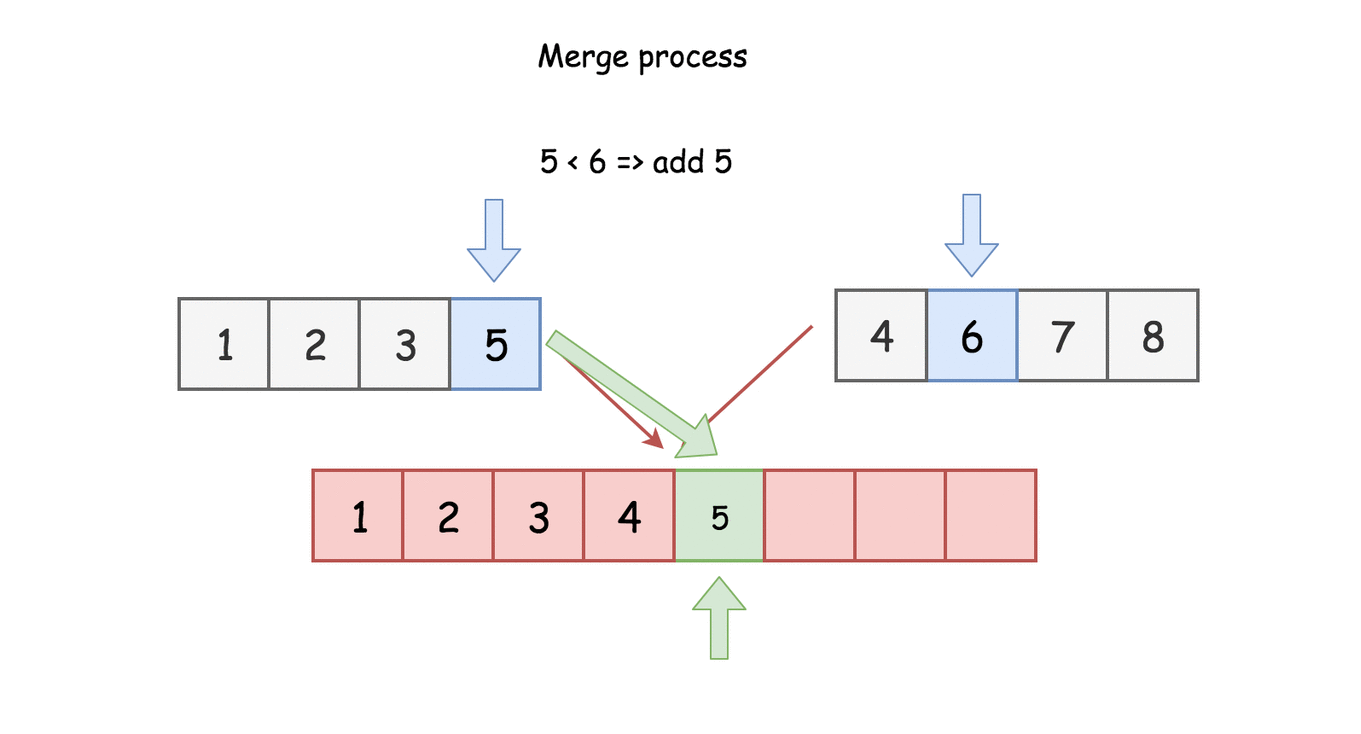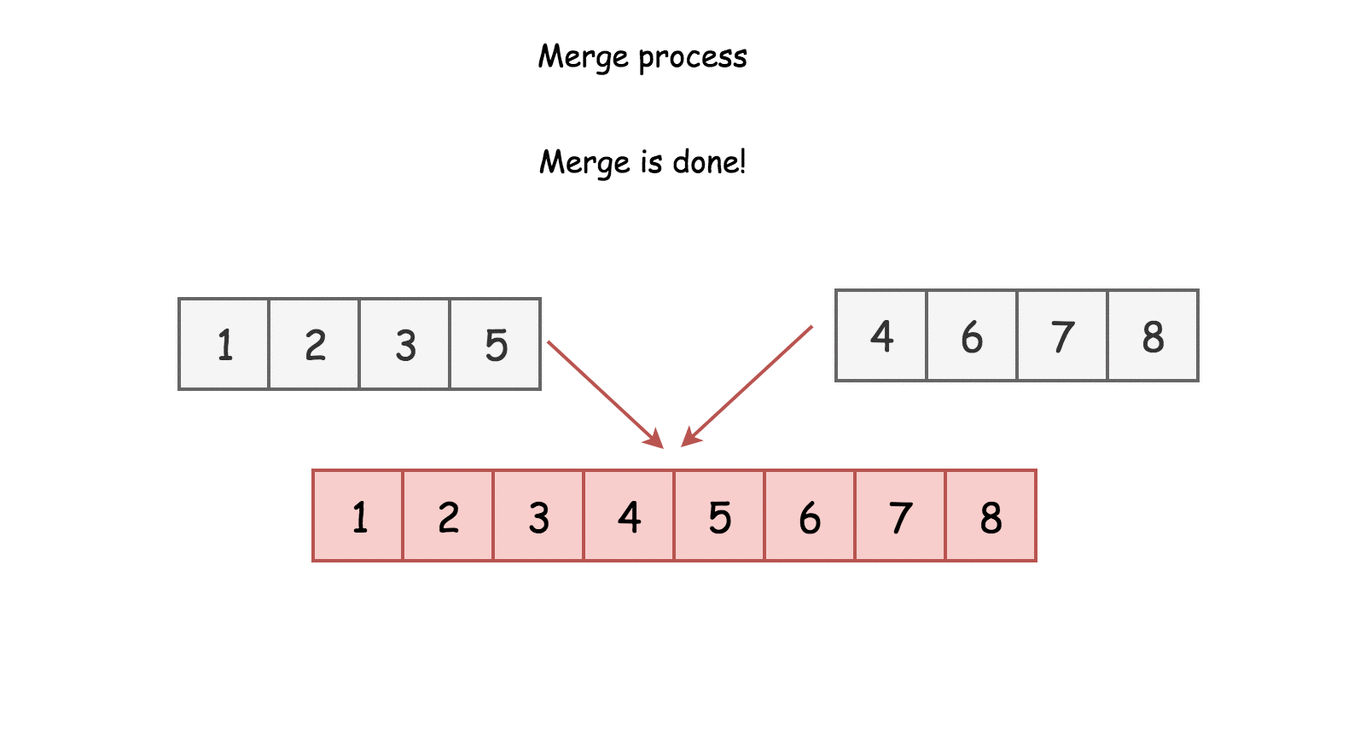
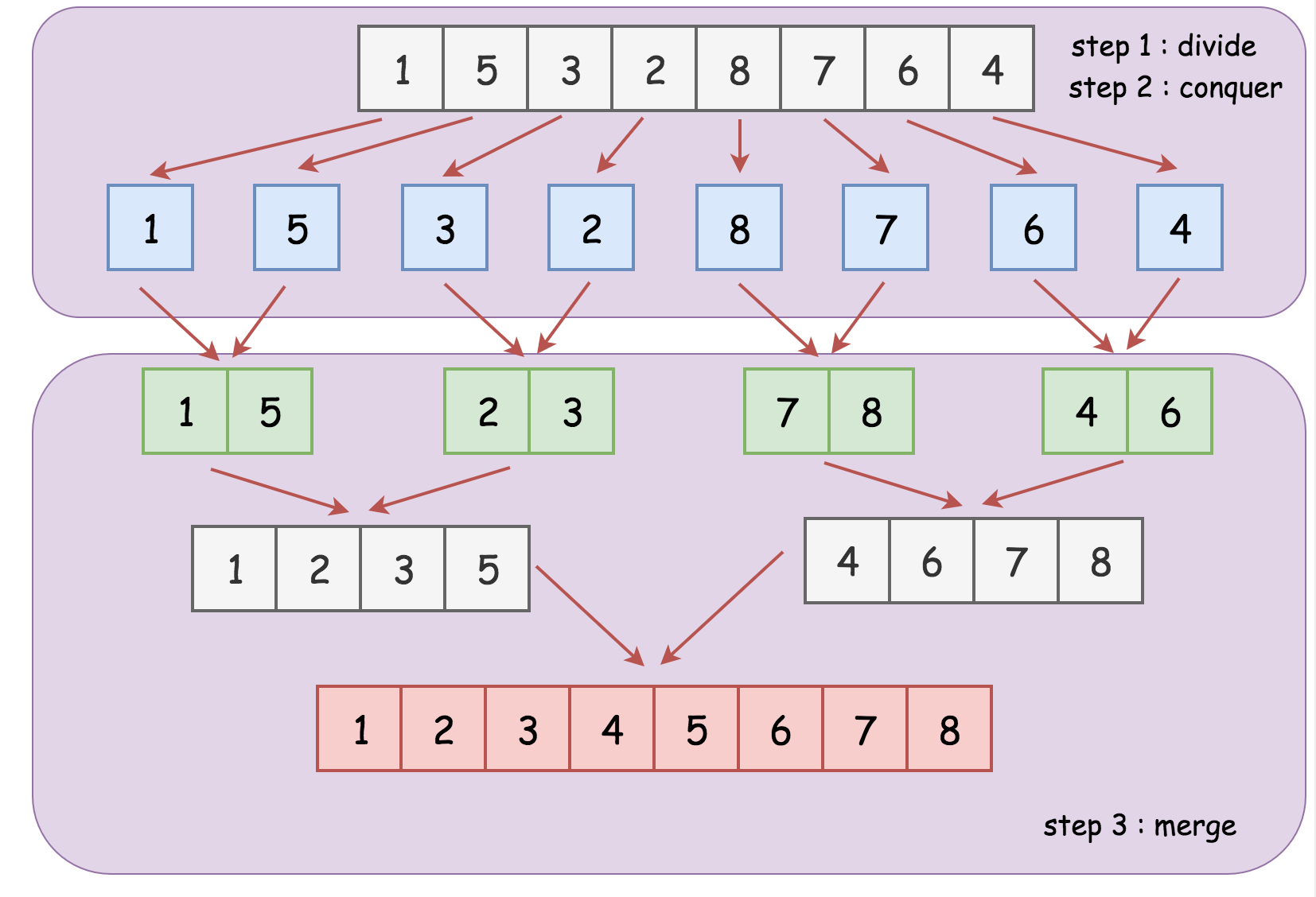
Bottom-up approach

In the bottom up approach, we divide the list into sublists of a single element at the beginning. Each of the sublists is then sorted already. Then from this point on, we merge the sublists two at a time until a single list remains.

The bottom up approach can be implemented iteratively.

Complexity

The overall time complexity of the merge sort algorithm is O(N log N).

1. We recursively divide the input list into two sublists until a sublist remains: we compute the midpoint O(1) and we repeat this steps N times until a single element remains. Since the array is halved at each level of recurison, this takes O(log n)
2. We repetively merge sublists until a single one remains, thus the merge operation takes linear time O(N) because it iterates over each element once to merge sorted sublist .

The Space Complexity is O(N), since we need to keep the sublists as well as the buffer to hold the merge results at each round of merge process.