Divide And Conquer - rFronteddu/general_wiki GitHub Wiki

• A divide-and-conquer algorithm works by recursively breaking the problem down into two or more subproblems of the same or related type, until these subproblems become simple enough to be solved directly 1(http://en.wikipedia.org/wiki/Divide-and-conquer_algorithm).
• Then one combines the results of subproblems to form the final solution.
• D&A is naturally implemented in the form of recursion.

There are in general three steps that one can follow in order to solve the problem in a divide-and-conquer manner.

1. Divide Divide the problem S into a set of subproblems: {S1, S2, ..., Sn} where n ≥ 2, i.e. there are usually more than one subproblem.
2. Conquer Solve each subproblem recursively.
3. Combine Combine the results of each subproblem.

Some classic examples are Merge Sort and Quick Sort.

Template

def divide_and_conquer( S ):
    # (1). Divide the problem into a set of subproblems.
    [S1, S2, ... Sn] = divide(S)

    # (2). Solve the subproblem recursively,
    #   obtain the results of subproblems as [R1, R2... Rn].
    rets = [divide_and_conquer(Si) for Si in [S1, S2, ... Sn]]
    [R1, R2,... Rn] = rets

    # (3). combine the results from the subproblems.
    #   and return the combined result.
    return combine([R1, R2,... Rn])

The essential part is to figure out the recurrence relationship between the subproblems and the original problem, which subsequently defines the functions of divide() and combine().

Application Example: Validate BST

Given a binary tree, validate if the given tree is a binary search tree (BST). The BST must meet all of the following properties:

• All values on the left subtree of a node should be less than the value of the node.
• All values on the right subtree of a node should be greater than the value of the node.
• Both the left and right subtrees must also be binary search trees.

The definition of BST is recursive in nature, making this a natural divide and conquer problem.

1. In the first step, we divide the tree into two subtrees -- its left child and right child. (Divide)
2. Then in the next step, we recursively validate each subtree is indeed a binary search tree. (Conquer)
3. Upon the results of the subproblems from Step 2, we return true if and only if both subtrees are both valid BST. (Combine)

The recursion in Step 2. would reach the base case where the subtree is either empty or contains a single node, which is a valid BST itself. We must also verified the two other properties

Application Example: Search a 2D Matrix

Write an efficient algorithm that searches for an integer value in an [mxn] matrix. This matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.
• Integers in each column are sorted in ascending from top to bottom.

Given the matrix, if we divide it into some sub-matrices by cutting it either by row and/or column, the resulting matrices would still keep the above two properties of the original matrix. Given the above insight, here is how we can apply the template to solve the problem.

1. We divide the matrix into 4 sub-matrices by choosing a pivot point based on a row and a column. (Divide)
2. Then we recursively look into each sub-matrix to search for the desired target. (Conquer)
3. If we find the target in either of the sub-matrices, we stop the search and return the result immediately. (Combine)

The base cases in the above recursion would be either the input matrix is empty or it contains only a single element. As a simple strategy, one can choose the middle point both on the row and column as the pivot points to divide the matrix.

Do we really need to look into each of the divided 4 sub-matrices? Notice that the smallest and the largest element of the input matrix is located in the top left and bottom right corner respectively, which also applies to each of the divided sub-matrices. In fact, we need to only look into 3 of the sub-matrices.

• If our target is equal to the pivot, we have found our target and immediately return the result.
• If our target is less than the pivot, we can discard the bottom-right sub-matrix. All elements in that region must be greater or equal than the pivot.
• If our target is greater than the pivot, we can discard the top-left sub-matrix. All elements in that region must be less than or equal than the pivot.

We can also pick a better pivot point

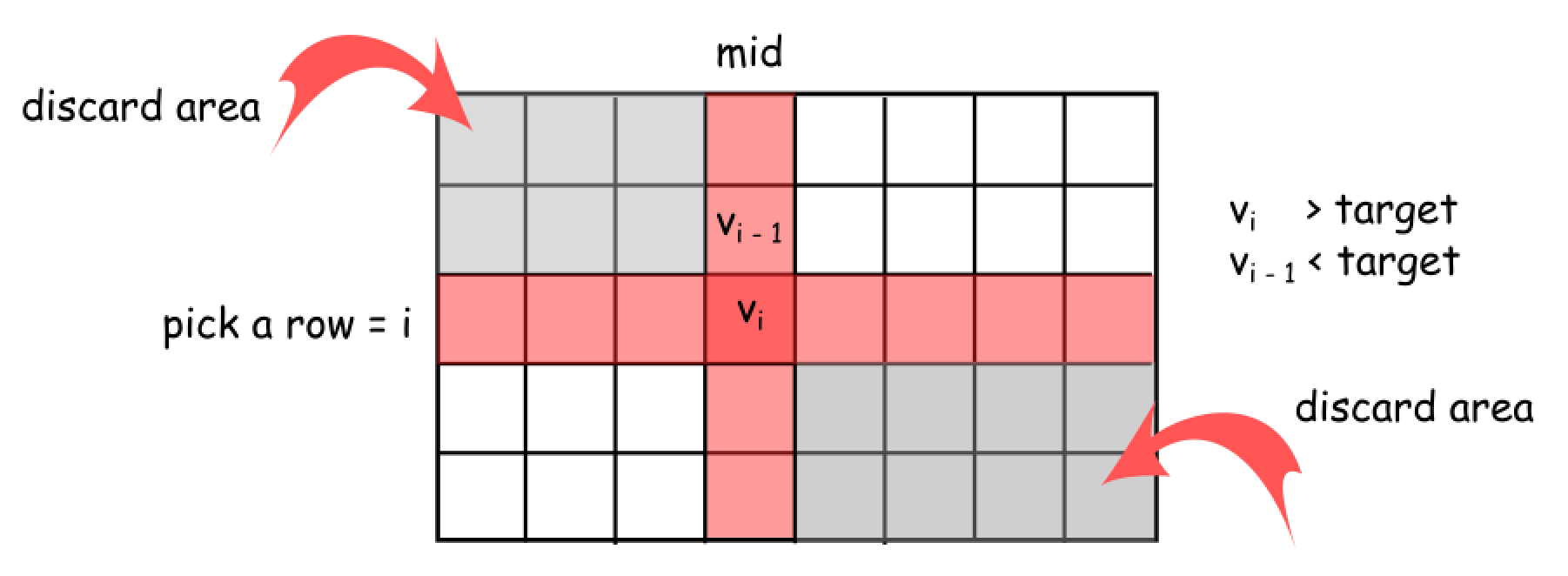
First, we choose the middle point on the column which divides the matrix into two sub-matrices. We then fix on this middle column to further determine an optimal row to divide the matrix. We scan the elements along the chosen middle column, to locate the boundary where the value of the element just goes beyond the target value, i.e. {$V_{i-1} < target < V_i$}. From this point, we divide the original matrix into 4 sub-matrices. And we just need to zoom into the bottom left and top right sub-matrices to look for the target value, while ignoring the top left and bottom right sub-matrices. We ignore the top left sub-matrix that ends with the element $V_{i-1}$, because all the elements within this sub-matrix would be less than the target value. Similarly, we ignore the bottom right sub-matrices that starts with the element $V_i$, because we know that all the elements within this sub-matrix would be greater than the target value.

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        // Check for edge cases
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return false;
        }
        
        return search (matrix, 0, matrix.length - 1, 0, matrix[0].length - 1, target);  
    }
    
    boolean search(int[][] matrix, int y0, int y1, int x0, int x1, int target) {
        if (y0 > y1 || x0 > x1) {
            return false;
        }
        
        int midY = (y0+y1)/2;
        int midX = (x1+x0)/2;
        int midEl = matrix[midY][midX];
        
        // If our target is equal to the pivot, we have found our target and 
        // immediately return the result.
        if (midEl == target) {
            return true;
        }
        
 
        if (midEl < target) {
            // Search bottom-right and the remaining submatrices
            return  search (matrix, midY + 1, y1, x0, x1, target) || 
                    search (matrix, y0, y1, midX + 1, x1, target);
        } else {
            // Search top-left and the remaining submatrices
            return  search (matrix, y0, midY - 1, x0, x1, target) ||
                    search (matrix, midY, y1, x0, midX - 1, target);
        } 
    }
}