Backtracking is a general algorithm for finding all (or some) solutions to some computational problems (notably Constraint satisfaction problems or CSPs), which incrementally builds candidates to the solution and abandons a candidate ("backtracks") as soon as it determines that the candidate cannot lead to a valid solution.

Conceptually, one can imagine the procedure of backtracking as the tree traversal.

• Starting from the root node, one sets out to search for solutions that are located at the leaf nodes.
• Each intermediate node represents a partial candidate solution that could potentially lead us to a final valid solution.
• At each node, we would fan out to move one step further to the final solution, i.e. we iterate the child nodes of the current node.
• Once we can determine if a certain node cannot possibly lead to a valid solution, we abandon the current node and backtrack to its parent node to explore other possibilities.

It is due to this backtracking behavior, that backtracking algorithms are often much faster than brute-force approaches since it eliminates many unnecessary exploration.

We are given a set of words represented in the form of a tree. The tree is formed such that every branch ends in a word. Our task is to find out if a given word is present in the tree.

Let's say we have to search for the word AIM. A very brute way would be to go down all the paths, find out the word corresponding to a branch and compare it with what you are searching for. You will keep doing this unless you have found out the word you were looking for.

In the diagram above our brute approach made us go down the path for ANT and AND before it finally found the right branch for the word AIM.

The backtracking way of solving this problem would stop going down a path when the path doesn't seem right. When we say the path doesn't seem right we mean we come across a node which will never lead to the right result. As we come across such node we back-track. That is go back to the previous node and take the next step.

In the above diagram backtracking didn't make us go down the path from node N. This is because there is a mismatch we found early on and we decided to go back to the next step instead. Backtracking reduced the number of steps taken to reach the final result. This is known as pruning the recursion tree because we don't take unnecessary paths.

One of the most classical problems that can be solved with the backtracking algorithm is the N-Queen puzzle.

he N-queens puzzle is the problem of placing N queens on a [N×N] chessboard such that no two queens can attack each other. One is asked to count the number of solutions to place the N queens on the board.

As a reminder, a queen can attack any piece that is situated at the same row, column or diagonal of the queue.

In order to count the number of possible solutions to place the N queens, we can break it down into the following steps:

1. Overall, we iterate over each row in the board, i.e. once we reach the last row of the board, we should have explored all the possible solutions.
2. At each iteration (we are located at a certain row), we then further iterate over each column of the board, along the current row. At this second iteration, we then can explore the possibility of placing a queen on a particular cell.
3. Before, we place a queen on the cell with index of (row, col), we need to check if this cell is under the attacking zone of the queens that have been placed on the board before. Let us assume there is a function called is_not_under_attack(row, col) that can do the check.
4. Once the check passes, we then can proceed to place a queen. Along with the placement, one should also mark out the attacking zone of this newly-placed queen. Let us assume there is another function called place_queen(row, col) that can help us to do so.
5. As an important behaviour of backtracking, we should be able to abandon our previous decision at the moment we decide to move on to the next candidate. Let us assume there is a function called remove_queen(row, col) that can help us to revert the decision along with the changes in step (4).

Now, with the above steps and functions, we can organize them in the form of recursion in order to implement the algorithm. In the following, we present the pseudocode of the backtracking algorithm.

def backtrack_nqueen(row = 0, count = 0):
    for col in range(n):
        # iterate through columns at the curent row.
        if is_not_under_attack(row, col):
            # explore this partial candidate solution, and mark the attacking zone
            place_queen(row, col)
            if row + 1 == n:
                # we reach the bottom, i.e. we find a solution!
                count += 1
            else:
                # we move on to the next row
                count = backtrack_nqueen(row + 1, count)
            # backtrack, i.e. remove the queen and remove the attacking zone.
            remove_queen(row, col)
    return count

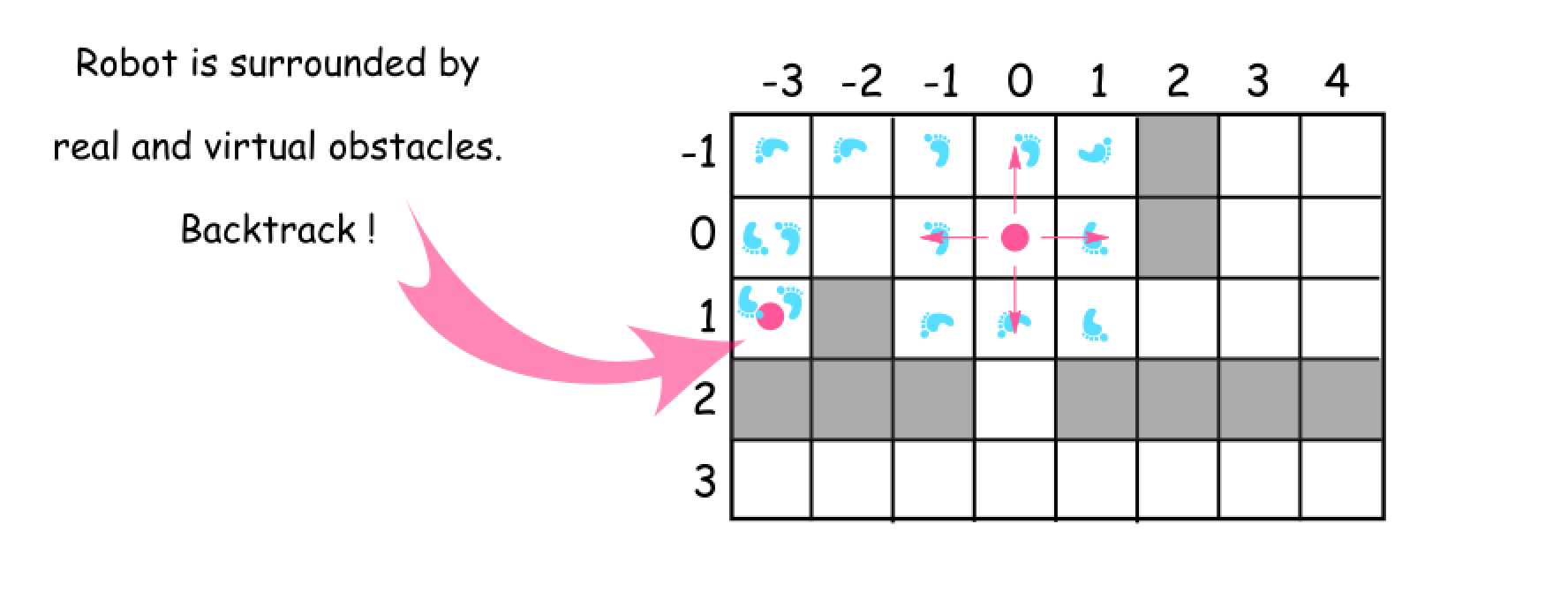
Given a room that is represented as a grid of cells, where each cell contains a value that indicates whether it is an obstacle or not, we are asked to clean the room with a robot cleaner which can turn in four directions and move one step at a time.

1. One can model each step of the robot as a recursive function (i.e. backtrack()).
2. At each step, the robot has four candidates of direction to explore, e.g. the robot located at the coordinate of (0, 0). Since not each direction is available though, one should check if the cell in the given direction is an obstacle or it has been cleaned before, i.e. is_valid(candidate). Another benefit of the check is that it would greatly reduce the number of possible paths that one needs to explore.
3. Once the robot decides to explore the cell in certain direction, the robot should mark its decision (i.e. place(candidate)). More importantly, later the robot should be able to revert the previous decision (i.e. remove(candidate)), by going back to the cell and restore its original direction.
4. The robot conducts the cleaning step by step, in the form of recursion of the backtrack() function. The backtracking would be triggered whenever the robot reaches a point that it is surrounded either by the obstacles (e.g. cell at the row 1 and the column -3) or the cleaned cells. At the end of the backtracking, the robot would get back to the its starting point, and each cell in the grid would be traversed at least once. As a result, the room is cleaned at the end.

• The following dfs method explores all four directions from the current cell, attempting to move in each direction.
• If the robot can move to a new cell in a particular direction, it proceeds with the exploration recursively.
• If the robot cannot move in a certain direction (due to obstacles or previously visited cells), it backtracks by rotating to the opposite direction, moving back to the previous cell, and rotating back to the original direction. This effectively implements the backtracking mechanism.
• Backtracking occurs when the robot exhausts all possible directions from the current cell or when it encounters obstacles. This ensures that the robot explores all reachable cells in the room.

class RobotRoomCleaner {
    private final Robot robot;
    private final Set<String> visited;
    private final int[][] directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}}; // Up, Right, Down, Left

    public RobotRoomCleaner(Robot robot) {
        this.robot = robot;
        this.visited = new HashSet<>();
    }

    public void cleanRoom() {
        dfs(0, 0, 0);
    }

    private void dfs(int x, int y, int direction) {
        String position = x + "," + y;
        if (visited.contains(position)) {
            return;
        }

        robot.clean();
        visited.add(position);

        for (int i = 0; i < 4; i++) {
            if (robot.canMove()) {
                int newX = x + directions[direction][0];
                int newY = y + directions[direction][1];

                dfs(newX, newY, direction);

                // Backtrack
                robot.turnLeft();
                robot.turnLeft();
                robot.move();
                robot.turnRight();
                robot.turnRight();
            }

            // Turn to next direction
            robot.turnRight();
            direction = (direction + 1) % 4;
        }
    }
}

The main idea of the game is to fill a grid with only the numbers from 1 to 9, while ensuring that each row and each column as well as each sub-grid of 9 elements does not contain duplicate numbers.

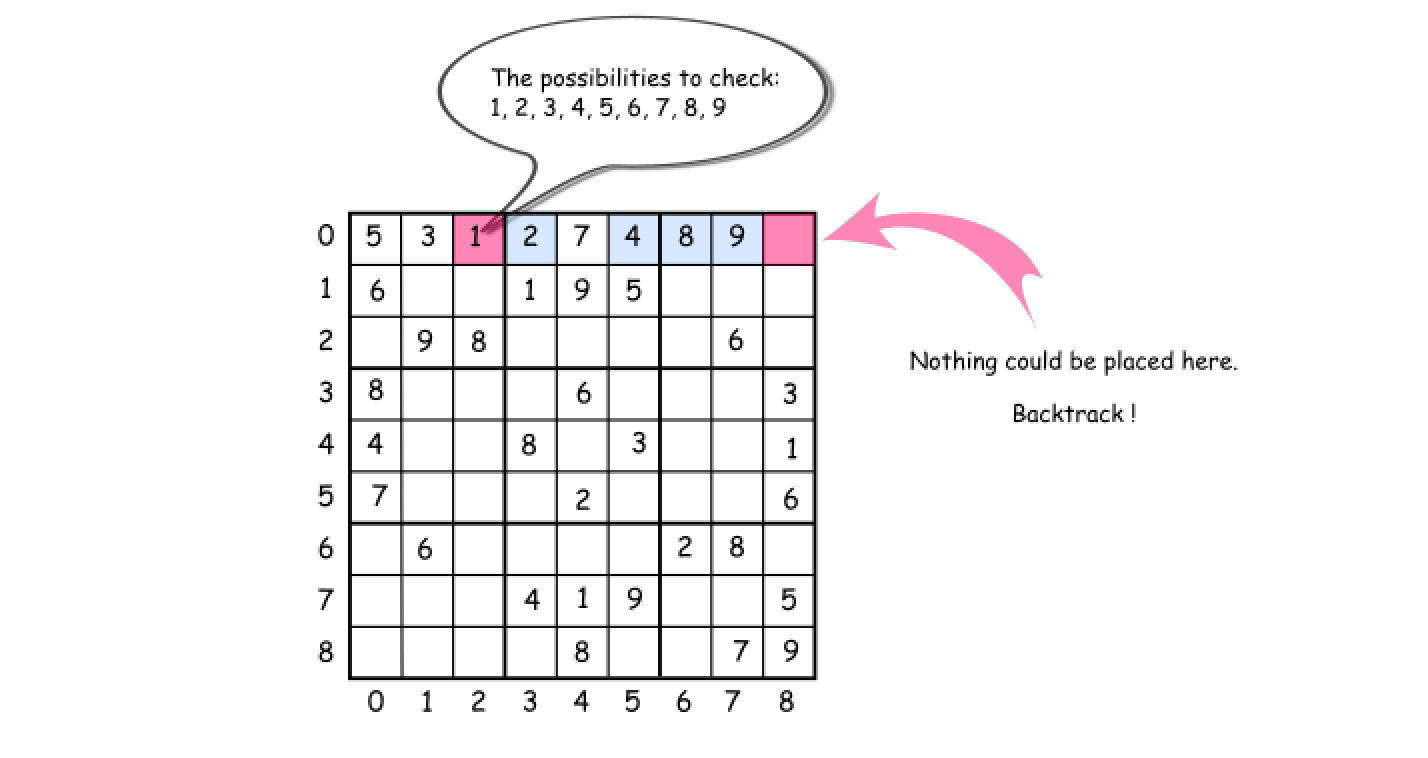
1. Given a grid with some pre-filled numbers, the task is to fill the empty cells with the numbers that meet the constraint of Sudoku game. We could model the each step to fill an empty cell as a recursion function (i.e. our famous backtrack() function).
2. At each step, technically we have 9 candidates at hand to fill the empty cell. Yet, we could filter out the candidates by examining if they meet the rules of the Sudoku game, (i.e. is_valid(candidate)).
3. Then, among all the suitable candidates, we can try out one by one by filling the cell (i.e. place(candidate)). Later we can revert our decision (i.e. remove(candidate)), so that we could try out the other candidates.
4. The solver would carry on one step after another, in the form of recursion by the backtrack function. The backtracking would be triggered at the points where either the solver cannot find any suitable candidate (as shown in the above figure), or the solver finds a solution to the problem. At the end of the backtracking, we would enumerate all the possible solutions to the Sudoku game.

class Solution {
    public void solveSudoku(char[][] board) {
        solve(board, 0, 0);
    }
    
    private void solve (char[][] board, int row, int col) {
        if (row == board.length) {
            // Reached end of rows, the solution is found
            return;
        }
        
        if (col == board[0].length) {
            // Reached end of columns in current row, move to next row
            solve(board, row + 1, 0);
            return;
        }      
        
        if (board[row][col] != '.') {
            // Cell already filled, move to next cell
            solve(board, row, col + 1);
            return;
        }
        
        for (char candidate = '1'; candidate <= '9'; candidate++) {
            board[row][col] = candidate;
            if (isValid (board, row, col)) {
                // If valid, move to next cell
                solve (board, row, col + 1);
                if (isSolved (board)) {
                    // If the board is solved, no need to continue
                    return;
                }
            }
            // Backtrack
            board[row][col] = '.';
        }
    }
    
    private boolean isSolved (char[][] board) {
        for (int row = 0; row < board.length; row++) {
            for (int col = 0; col < board[0].length; col++) {
                if (board[row][col] == '.') {
                    // If any cell is empty, the board is not solved
                    return false;
                }
                if (!isValid(board, row, col)) {
                    // If any cell violates Sudoku rules, the board is not solved
                    return false;
                }
            }
        }
        // If all cells are filled and valid, the board is solved
        return true;
    }
    
    private boolean isValid (char[][] board, int row, int col) {
        // Each digits 1-9 once in each row.
        // Each digits 1-9 once in each column.
        // Each digits 1-9 once in each 3x3 sub-boxes of the grid.
        
        char candidate = board[row][col];
        
        // row check
        for (int i = 0; i < board[0].length; i++) {
            if (board[row][i] == candidate && i != col) {
                return false;
            }
        }
        
        // col check
        for (int i = 0; i < board.length; i++) {
            if (board[i][col] == candidate && i != row) {
                return false;
            }
        }
        
        // 3x3 square
        int startRow = row - (row % 3);
        int startCol = col - (col % 3);
        for (int i = startRow; i < startRow + 3; i++) {
            for(int j = startCol; j < startCol + 3; j++) {
                if (board[i][j] == candidate && (i != row || j != col)) {
                    return false;
                }
            }
        }
        return true;
    }
}

def backtrack(candidate):
    if find_solution(candidate):
        output(candidate)
        return
    
    # iterate all possible candidates.
    for next_candidate in list_of_candidates:
        if is_valid(next_candidate):
            # try this partial candidate solution
            place(next_candidate)
            # given the candidate, explore further.
            backtrack(next_candidate)
            # backtrack
            remove(next_candidate)