Weekz 11 Classification Decision Trees - pointOfive/stat130chat130 GitHub Wiki

Machine Learning

Tutorial/Homework: Topics

Tutorial/Homework Extensions/New Topics for Lecture

These are topics introduced in the lecture that build upon the tutorial/homework topics discussed above

Out of scope:

Additional classification metrics and additional considerations around confusion matrices beyond those discussed above [previously, "Material covered in future weeks"]
Deeper details of Decision Tree and Random Forest construction (model fitting) processes [previously, "Anything not substantively addressed above"]
...the actual deep details of log odds, link functions, generalized linear models, and now multi-class classification since we can instead just use .predict() and we now know about predict_proba()...
...other Machine Learning models and the rest of scikit-learn, e.g., K-Folds Cross-Validation and model complexity regularization tuning with sklearn.model_selection.GridSearchCV, etc.

Tutorial/Homework: Topics

Classification Decision Trees

Decision Trees predict the value of an outcome based on the sequential application of rules relative specific predictor variables. In the first, "It's mine / I don't want it" example below, the first level of the Tree is a predictor variable, the second level is the rule, and the final level is the outcome prediction. This particular "cat example" Decision Tree intends to represent a humorous infinite loop so it's a bit ill-defined as far as outcome predictions and predictor variables are concerned, but it conveys the basic idea of a Decision Tree. A more true example of Decision Tree is provided after the first example.

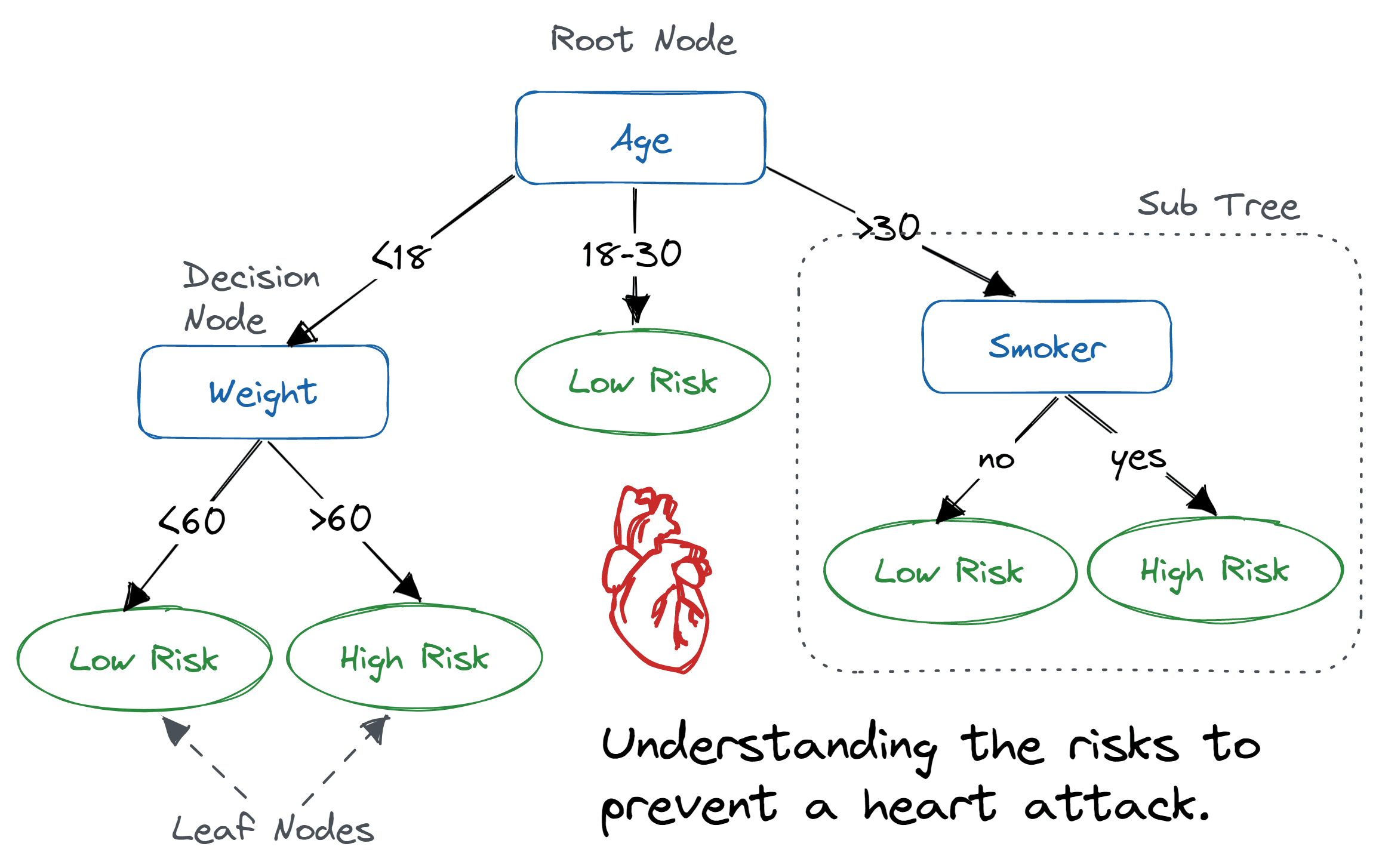The predictor variables in the Decision Tree above are "Age", "Weight", and "Smoking" status. And the decision rules are choices based on each of these, with the decision rules attached to "Weight" and "Smoking" occurring after the decision rules associated with "Age" (and therefore representing an interaction in the same manner as previously encountered in Multiple Linear Regression). While it may at first seem strange, it would be possible to repeatedly re-use the same predictor variables with different decision rules in the same Decision Tree. This can actually be quickly seen by the fact that, unlike the example above which has three possible outcomes for the decision rule associated "Age", most Decision Tree are actually so-called Binary Decision Trees which means each node has only a "left" and "right" decision rule. So if the "cancer risk" Decision Tree above were to be re-expressed as a Binary Decision Trees the first decision rule would only be >30 or not which would point "left" to the same "Age" variable which would then split on <18 where the 18-30 would point to the "right" to "Low Risk" and the "left" decision would then point to the currently existing decision rule for "Weight".

Classification versus Regression

The outcomes predicted by Decision Trees can be numeric or categorical.

Multiple Linear Regression is used to predict a continuous outcome whereas Logistic Regression is used to predict a binary categorical outcome, and linear models for general categorical outcomes are possible.
Decision Trees are most frequently deployed as Classification Decision Trees which are used to predict a binary categorical outcome but they may also be deployed as Regression Decision Trees which are used to predict a continuous outcome, and Multi-Class Classification Decision Trees for general categorical outcomes are an extremely natural extension of Binary Classification Decision Trees.

Prediction of numeric outcomes is referred to as regression.

Regression may therefore be used as a more general term and need not specifically refer to the specific methodologies of Simple or Multiple Linear Regression, and indeed regression in general certainly does not refer to Logistic Regression which (perhaps confusingly) is a specific classification methodology.
The (perhaps misnomered) titling of Logistic Regression is historical and references the similar linear specification framework that Logistic Regression shares with Simple and Multiple Linear Regression.

Prediction of categorical outcomes is referred to as classification.

Classification can refer to both binary or multi-class classification, but typically refers to the former while the latter is generally explicitly indicated when desired.

scikit-learn versus statsmodels

The statsmodels library provides hypothesis testing and inference for Multiple Linear Regression, Logistic Regression, and other statistical models. In contrast, scikit-learn (or synonymously sklearn) provides NEITHER statistical hypothesis testing NOR statistical inference despite providing many linear models, including Multiple Linear Regression and Logistic Regression.

This difference between statsmodels and sklearn may at first seem especially strange given the generally nearly analogous interfaces provided by both packages. Namely, both proceed on the basis of the same, "first specify, then fit, and finally use the model (for analysis or prediction)" deployment template. The reason for the contrasting distinction, then, is due to a deep differences between the perspectives of these two libraries. For you see while statsmodels is concerned with the (statistical hypothesis testing and inference) functionality of statistical models, sklearn instead approaches the problem from the perspective of Machine Learning which only concerns itself with the raw predictive performance capability of a model (and hence is unconcerned with statistical hypothesis testing and inference).

from sklearn import datasets
import pandas as pd
import statsmodels.formula.api as smf
from sklearn.linear_model import LinearRegression

cancer_data = datasets.load_breast_cancer()
cancer_df = pd.DataFrame(data=cancer_data.data, 
                         columns=cancer_data.feature_names)

MLR = smf.ols("Q('mean area') ~ Q('mean fractal dimension') + Q('smoothness error')", 
              data=cancer_df)
MLR_fit = MLR.fit()  # Fit the mulitple lienar regression model (MLR)
display(MLR_fit.summary())  # Hypothesis Testing and Inference

MLR2 = LinearRegression()
MLR2_fit = MLR2.fit(X=cancer_df['mean fractal dimension','smoothness error'](/pointOfive/stat130chat130/wiki/'mean-fractal-dimension','smoothness-error'), 
                    y=cancer_df['mean area'])
print(MLR2.intercept_, MLR2.coef_)  # NEITHER Hypothesis Testing NOR Inference 
# Both estimated coefficients agree
# Both predictions agree
print(MLR_fit.predict(cancer_df['mean fractal dimension','smoothness error'](/pointOfive/stat130chat130/wiki/'mean-fractal-dimension','smoothness-error').iloc[:2,:]),
      MLR2_fit.predict(cancer_df['mean fractal dimension','smoothness error'](/pointOfive/stat130chat130/wiki/'mean-fractal-dimension','smoothness-error').iloc[:2,:]))

The notion that raw predictive performance and statistical inference are "orthogonal" to each other (by which we mean they are distinct and independent of each other in some sense) was previously encountered in the example of multicollinearity. As discussed in the previous chapter, high multicollinearity reduces the ability of a model to provide precise statistical inference, but it does not necessarily imply a degradation of a model's predictive performance (although excessively high multicollinearity can indeed eventually lead to catastrophic model overfitting if left completely unchecked).

But what then does the Machine Learning framework actually contribute over statistical models which are already "predictive models"? Well, by replacing the focus on statistical inference with a preoccupation on raw predictive performance, Machine Learning naturally sought to increase model complexity and sophistication.

But now as you may recall from the same discussion from the previous chapter surrounding multicollinearity, increased model complexity is precariously tied to model overfitting. So how can this precipitous and perilous risk be addressed?

The answer provided by Machine Learning is to use incredibly complex models but to then regularize them. By "regularize them", which we call regularization, what we mean is that despite a model being incredible complex, we can still limit their expressibility by constraining a model fit in certain ways. To get a sense of what such regularization might mean, in the case Multiple Linear Regression or Logistic Regression one form of regularization would be to enforce limitations on how big the magnitudes of estimated coefficient parameters are allowed to be.

So what the Machine Learning framework provides beyond the classical statistical inference paradigm is the introduction of model complexity tuning parameters which extend predictive models in a manner that enables their regularization. This then actualizes the (now) "classic Machine Learning process" of optimizing (or tuning) the predictive performance of incredibly complex models through the process of model complexity regularization tuning (which is done as part of model fitting process). Therefore, while the statsmodels library is focussed on providing statistical hypothesis testing and inference, the Machine Learning sklearn library is completely unconcerned with this. Instead, all the functionality of the sklearn library revolves around regularization strategies, the associated model complexity parameters, and their tuning for the purposes of RAW predictive performance alone. Machine Learning reimagines the objective of providing statistical evidence and inference into the objective of just being AMAZINGLY GREAT at prediction. And fair enough. It's not a bad idea. But there are a few more considerations that we'll need to put in place before we'll really see the brilliance of this alternative Machine Learning perspective.

The code below gives an example of how Machine Learning works for a Classification Decision Tree. The "deeper" a Classification Decision Tree is the more complex and sophisticated predictions are. Indeed, every subsequent level in a Classification Decision Tree represents an additional interaction (of all the previous rules AND the new decision rule introduced with the new Classification Decision Tree depth level). But this is increased complexity is a double-edged sword because it can quickly become overfit to the data at hand, finding idiosyncratic associations in the dataset which do not actually generalize outside of the dataset. The Machine Learning strategy here is the regularize the Classification Decision Tree to a model complexity (controlled by the tree depth) that appropriately finds generalizable associations without overfitting.

from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt
import numpy as np

# Make Benign 0 and Malignant 1
# JUST RUN THIS ONCE!!
cancer_data.target = 1-cancer_data.target 
cancer_data.target_names = np.array(['Benign\n(negative)','Malignant\n(positive)'])

# Increase for more Model Complexity
Model_Complexity_Tuning_Parameter = 5 
# Decrease to for more Regularization

# Initialize and train the Decision Tree classifier
clf = DecisionTreeClassifier(max_depth=Model_Complexity_Tuning_Parameter, random_state=42)
clf.fit(X=cancer_df, y=cancer_data.target)
# The outcome has changed compared to the earlier multiple linear regression model...

plt.figure(figsize=(12, 4), dpi=200)
plot_tree(clf, feature_names=cancer_data.feature_names.tolist(), 
          class_names=cancer_data.target_names.tolist(), 
          filled=True, rounded=True)
plt.title("Decision Tree (Depth = "+str(Model_Complexity_Tuning_Parameter)+")")
plt.show()

Feature Importances

Unlike with linear models which have some interpretable mathematical expression which determines predictions, predictions from Decision Trees require the traversal down a tree based on a number of decision rules made at each node of the tree. Another difference is that there are no coefficient parameters which indicate the nature of the relationship between the outcome and predictor variables. Instead, in a Decision Trees it's the decision rules encountered at each node in the traversal down a tree which capture the nature of the relationship between the outcome and predictor variables.

Interestingly, the way predictions are made in Decision Trees actually offers an additional opportunity to understand the relationship of the outcome and predictor variables in a manner that does not immediately come to mind when considering the linear prediction form of a linear model. Besides just "reading down the tree" to understand how the outcome is driven by predictor variables, since each decision rule in the tree "explains" (in some manner) some amount of the outcomes in the data, we can determine the proportion of the explanation of the outcomes in the data that should be attributable to each predictor variables (since each decision rule is attached to a single predictor variable).

import plotly.express as px

feature_importance_df = pd.DataFrame({
    'Feature': cancer_data.feature_names.tolist(),
    'Importance': clf.feature_importances_
}).sort_values(by='Importance', ascending=False).reset_index()

fig = px.bar(feature_importance_df[:15], y='Feature', x='Importance', 
             title='Feature Importance')
fig.show()

# #https://stackoverflow.com/questions/52771328/plotly-chart-not-showing-in-jupyter-notebook
# import plotly.offline as pyo
# # Set notebook mode to work in offline
# pyo.init_notebook_mode()

Confusion Matrices

First, what does just being AMAZINGLY GREAT at prediction mean? Let's consider this question in the context of classification. Here, we're concerned with predicting a binary outcome, and it's customary to refer to an outcome of $1$ as a positive and correspondingly, an outcome of $0$ as a negative (even if that's not quite right). A positive or negative prediction then can be true or false, which leads to the following possibilities, the consideration of which is known as a confusion matrix.

	Predicted "Negative"	Predicted "Positive"
Actually "Negative"	True Negative (TN)	False Positive (FP)
Actually "Positive"	False Negative (FN)	True Positive (TP)

Metrics

There are a great variety of so-called metrics by which the confusion matrix may be examined. The following are the "most common metrics" that students will initially come across. But certainly the many different metrics even beyond these each have their own particular use-cases and purposes depending on the specific contexts at play.

Accuracy measures the proportion of true results (both true positives and true negatives) in the population.

$$\text{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN}$$

Sensitivity measures the proportion of actual positives that are correctly identified.

$$\text{Sensitivity} = \frac{TP}{TP + FN}$$

Specificity measures the proportion of actual negatives that are correctly identified.

$$\text{Specificity} = \frac{TN}{TN + FP}$$

Precision measures the proportion of positive identifications that were actually correct.

$$\text{Precision} = \frac{TP}{TP + FP}$$

You have already seen in the link above how many different metrics there are. This is because of how many different applications are interested in classification and then results from the nature of the differences in the objectives and priorities of these different domains. It's worse than that though as there are many synonyms and highly related terminologies.
For example, Sensitivity is also called Recall, and there is something call the ROC curve which usually visualizes Sensitivity versus Specificity, but there is also the alternative Recall-Precision curve visualizes which Sensitivity (i.e., Recall) versus Specificity. And Sensitivity and Recall are also called the True Positive Rate whereas Specificity is called the True Negative Rate. The False Positive Rate is 1-True Negative Rate (or 1- Specificity) and the False Negative Rate is 1-True Positive Rate (or 1- Sensitivity or (or 1- Recall)). The False Positive Rate is also the same concept as Type I error $\alpha$ in hypothesis testing while the False Negative Rate is also the same concept as Type II error $\beta$ in hypothesis testing. Indeed, there are a lot of concepts, and a lot of terminology, and a lot of relationships and equivalences, and it can indeed get very confusing very quickly if you let it!

In Sample Versus Out of Sample

Obviously we'd prefer for most predictions made by a model to be True rather than False with respect to the confusion matrix of the previous section. But here we have a second question to ask. Namely, for what data do we REALLY care about the predictions being True rather than False? And the answer is: we really only care about predictions for new data since we don't need predictions for the data we already have. This consideration was discussed previously last week and is concerned with the notion of "in sample" versus "out of sample" model performance. Respectively, this refers to data used to fit the model (which we'd expect the model to be able to predict fairly well since it's already "seen" this data) and new data not used to fit the model (which present a much more interesting prediction proposition for the model since "it's being asked make predictions for new data it hasn't seen before").

The "in sample" versus "out of sample" consideration is also known as the train-test framework. In sklearn this functionality is available through train_test_split but it is also possible to just use the pandas .sample(...) method.

from sklearn.model_selection import train_test_split
import numpy as np

np.random.seed(130)
training_indices = cancer_df.sample(frac=0.5, replace=False).index#.sort_values()
testing_indices = cancer_df.index[~cancer_df.index.isin(training_indices)]
print(training_indices)
print(testing_indices)

np.random.seed(130)
train,test = train_test_split(cancer_df, train_size=0.5)
print(train.index)  
print(test.index)

Try out the code below to determine what level of model complexity leads to the best out of sample predictive performance.

import seaborn as sns
from sklearn.metrics import confusion_matrix

# Increase for more Model Complexity
Model_Complexity_Tuning_Parameter = 2 
# Decrease to for more Regularization

# Initialize and train the Decision Tree classifier
clf = DecisionTreeClassifier(max_depth=Model_Complexity_Tuning_Parameter, random_state=42)
clf.fit(X=cancer_df.iloc[training_indices, :], y=cancer_data.target[training_indices])
# The outcome has changed compared to the earlier multiple linear regression model...

plt.figure(figsize=(12, 4), dpi=200)
plot_tree(clf, feature_names=cancer_data.feature_names.tolist(), 
          class_names=cancer_data.target_names.tolist(), 
          filled=True, rounded=True)
plt.title("Decision Tree (Depth = "+str(Model_Complexity_Tuning_Parameter)+")")
plt.show()

# Predict on the test set
y_pred = clf.predict(cancer_df.iloc[testing_indices, :])

# Generate the confusion matrix
conf_matrix = confusion_matrix(cancer_data.target[testing_indices], y_pred)

# Get the target names for 'benign' and 'malignant'
target_names = cancer_data.target_names.tolist()

# Set up a confusion matrix with proper labels using target names
plt.figure(figsize=(6, 4))
sns.heatmap(conf_matrix, annot=True, fmt='d', cmap='Blues', 
            xticklabels=[f'Predicted {label}' for label in target_names], 
            yticklabels=[f'Actually {label}' for label in target_names])

plt.title('Confusion Matrix (Depth = '+str(Model_Complexity_Tuning_Parameter)+')')
plt.xlabel('Predicted Label')
plt.ylabel('True Label')

# Add custom labels for FP, FN, TP, and TN
plt.text(0.5, 0.1, "True Negative (TN)", fontsize=12, color='red', ha='center', va='center')
plt.text(1.5, 0.1, "False Positive (FP)", fontsize=12, color='red', ha='center', va='center')
plt.text(0.5, 1.1, "False Negative (FN)", fontsize=12, color='red', ha='center', va='center')
plt.text(1.5, 1.1, "True Positive (TP)", fontsize=12, color='red', ha='center', va='center')

plt.show()

Tutorial/Homework/Lecture Extensions

Model Fitting: Decision Trees Construction

The process of model fitting for a Decision Tree is the determination of which rules based on predictor variables best predict the outcome variables for a given dataset.

This model fitting process actually just amounts to the "exhaustive" search of every possible decision rule that could be added to an existing Decision Tree, and then constructing the Decision Tree by adding the identified "optimal" rule to sequentially "grow" the Decision Tree.
The "sequentially optimal" nature of this Decision Tree construction process makes this model fitting process a so-called "greedy search algorithm", where the meaning of "optimality" must be defined according to some "arbitrary" criterion.
In the case of regression the "arbitrary" criterion determining "optimality" is typically mean squared error (which is just an ever-so-slight reformulation of $R^2$) along with a so-called complexity penalty or stopping rule (which we shall discuss soon).

$$R^2 = \frac{\sum_{i}(y_{i}-\hat y_{i})^{2}}{\sum_{i}(y_{i}-{\bar {y}})^{2}} \quad \quad MSE = \frac{\sum_{i}(y_{i}-\hat y_{i})^{2}}{n}$$

In the case of classification the "arbitrary" criterion determining "optimality" is typically Gini impurity or Shannon entropy again along with with a so-called complexity penalty or stopping rule (which again we shall discuss soon).

Model Complexity and Machine Learning

The section above comparing and contrasting scikit-learn and statsmodels introduces the Machine Learning paradigm as a re-imagination of the domain of classic statistical inference. In some senses Machine Learning extends traditional statistical modeling.

Machine Learning models literally extend statistical models with regularization tuning parameters
which in turn allows for greatly improved out of sample predictive performance over traditional statistical modeling.

Of course, on the other hand, the adjusted focus towards predictive performance solely which Machine Learning pursues comes at a cost. Machine Learning loses and does not offer an alternative path towards the characterization of statistical evidence regarding understanding of parameters for the purposes of hypothesis testing or inference. And it's not the case that these tools have suddenly become obsolete through the conceptualizations of Machine Learning. Rather, what's really happening is that we can now understand that there exists a spectrum of data modeling, on one side of which lies "interpretability" of the "linear model" form, while on the other lies the pursuit of raw predictive performance.

Last week contrasted Evidence-based Model Building with Performance-based Model Building and therefore arrived at an initial introduction to the topics of Complexity, Multicollinearity, and Generalizability. We'll now return to illustrating and considering these concepts through the specific example of Classification Decision Trees. This allows us to concretely examine the perspective of Machine Learning which views predictive performance through the lens of Model Complexity.

It's not unusual to mistake Decision Trees for a simple model when they're first encountered. But Decision Trees are in fact incredibly complex models. Have a look at the Decision Trees produced by the following code for a data that's trying to predict the genre of a newspaper article. If the increasing scale alone of the number of decision rules of the increasingly "deep" Decision Trees doesn't along convince you, have a look at the out of sample accuracy metric of the predictive performance of these models and you'll see that Decision Trees can quickly become super overfit to the data they're trained on, demonstrating the utterly incredible complexity potential of the Decision Tree models.

from sklearn.datasets import fetch_20newsgroups_vectorized
newsgroups_vectorized = fetch_20newsgroups_vectorized(subset='train')
newsgroups_vectorized_test = fetch_20newsgroups_vectorized(subset='test')

for depth in np.logspace(1, 5, num=5, base=2, dtype=int):
    newsboys = DecisionTreeClassifier(max_depth=depth, random_state=42)
    newsboys.fit(X=newsgroups_vectorized.data, 
                 y=newsgroups_vectorized.target)

    plt.figure(figsize=(12, 4), dpi=200)
    plot_tree(newsboys, feature_names=newsgroups_vectorized.feature_names.tolist(), 
              class_names=newsgroups_vectorized.target_names, 
              filled=True, rounded=True)
    plt.title("Decision Tree (Depth = "+str(depth)+")")
    plt.show()

    print("In sample accuracy",
      (newsboys.predict(newsgroups_vectorized.data)==newsgroups_vectorized.target).sum()/len(newsgroups_vectorized.target),
      "\nOut of sample accuracy",
      (newsboys.predict(newsgroups_vectorized_test.data)==newsgroups_vectorized_test.target).sum()/len(newsgroups_vectorized_test.target))

This example of Decision Trees perfectly illustrates what the idea of Machine Learning is. Machine Learning introduces models which can be made incredibly complex such as Decision Trees and then uses regularization tuning parameters to determine what the appropriate complexity of the model should be for a given dataset to all the predictive performance of the model to generalize to the out of sample context. In the example here, the regularization tuning parameter used is the max_depth of the constructed Decision Tree, but other alternative regularization tuning parameter options for Decision Trees are

min_samples_split
min_samples_leaf
min_weight_fraction_leaf
max_features
max_leaf_nodes
min_impurity_decrease

and

ccp_alpha

The meaning of these regularization tuning parameters can be examined by looking at the documentation provided when DecisionTreeClassifier? is run. But what can be said in general of the first group of regularization tuning parameters is that they are all so-called stopping rules meaning that they specify hard constraints which limit the model fitting process. On the other hand, the ccp_alpha is a slightly different kind of regularization tuning parameter in that it measures the complexity of a fitted Decision Tree and then chooses a final Decision Tree as a tradeoff between this complexity and the in sample predictive performance of the Decision Tree.

The ccp_alpha regularization tuning parameter is described as follows:

Complexity parameter used for Minimal Cost-Complexity Pruning. The subtree with the largest cost complexity that is smaller than ccp_alpha will be chosen. By default, no pruning is performed. See "minimal_cost_complexity_pruning" for details.

A regularization tuning parameter like ccp_alpha which adds a model complexity penalization to in sample predictive performance represents a very typical Machine Learning strategy. In this strategy a spectrum of models with different in sample predictive performances can be considered by "dialing in" to different model complexities based on a model complexity penalization choice. All these models can then be test on out of sample predictive performance and the "best" model can then be chosen.

The basic idea of choosing "the best model" by testing the out of sample predictive performance using a test dataset if of course though the fundamental methodology used by Machine Learning to identify "optimal" predictive performance. In the example above, of the choices available, it seems the tree depth of 8 offers good generalizability of predictive performance with a training accuracy of ~28% compared to a testing accuracy of ~26%.
The generalizability of predictive performance greatly deteriorates from there. However, even without the consistent generalizability of predictive performance, the the tree depth of 32 is able to achieve ~45% accuracy. So in terms of raw predictive performance, it seems the "deeper" Decision Tree model may still be preferred.

Machine Learning does a little bit more than this tough. Machine Learning is the introduction of the idea that algorithms can be used to create data prediction models. Here's an idea call Random Forests: make hundreds of different Decision Trees using bootstrapped samples and then average the predictions from all the Decision Trees. Here's the performance that an "algorithmic" model like this can provide. Spoiler: no linear model can even get close to matching the predictive performance of Random Forests.

from sklearn.ensemble import RandomForestClassifier

# Fit 1000 Decision Trees with a max depth of 16 and use their average predictions
rfc = RandomForestClassifier(n_estimators=1000, max_depth=16, random_state=1)
rfc.fit(X=newsgroups_vectorized.data, 
        y=newsgroups_vectorized.target)

print("In sample accuracy",
      (rfc.predict(newsgroups_vectorized.data)==newsgroups_vectorized.target).sum()/len(newsgroups_vectorized.target),
      "\nOut of sample accuracy",
      (rfc.predict(newsgroups_vectorized_test.data)==newsgroups_vectorized_test.target).sum()/len(newsgroups_vectorized_test.target))

Prediction

While not directly emphasized so far, the .predict(X) method of a fitted model has started to make an appearance in the context of Machine Learning. In the contexts of Multiple Linear Regression and Logistic Regression the focus of prediction is always on the linear form of the model since this defines the predictions. However, it has always been possible to make predictions from these models using their .predict(X) methods once the models have been fit.

import statsmodels.api as sm
# using this above for convenience of 
# demonstration rather than the usual
# import statsmodels.formula.api as smf

MLR_fit.predict(cancer_df)

X = (cancer_df-cancer_df.mean())/cancer_df.std()
y = cancer_data.target
LR_fit = sm.Logit(exog=X, endog=y).fit()
display(LR_fit.summary())
LR_fit.predict(X)

These of course show in sample training prediction so these two demonstrations are not concerned with out of sample predictive performance in their current forms. Rather, they are simply making the predictions of the linear forms of their models. Well, at least the Multiple Linear Regression model is. The Logistic Regression model, as you might remember, is wrapped around a linear model form but then this needs to get transformed into a probability prediction (and that's what the so-called inverse logit transformation of the so-called log-odds of the linear form of the Logistic Regression model does). In the case of Logistic Regression then, if we want to visualize the predictions in terms of its probability predictions, then we need to .predict(X) method of the fitted Logistic Regression model. Otherwise, it's a bit too advanced for us at the moment to try to figure out how we need to transform the fitted linear form of the Logistic Regression model to get its probability predictions.

Both sklearn and statmodels fitted model objects have .predict(X) methods. So indeed, as we have already seen, the Decision Tree and Random Forest models encountered above likewise have .predict(X) methods. Examples are given below for completeness, but here note that these are the predictions for out of sample data in the manner prescribed by Machine Learning.

And there is one more important and interesting thing to note. The predictions for Logistic Regression above were noted as being, and can be seen to be probabilities (although in the example above most of the probabilities are close to 0 and 1). But the predictions below are integers, 0 and 1 for clf, and integers representing newspaper articles in the case of the latter two (newsboys and rfc) classification models.

clf.predict(cancer_df.iloc[testing_indices, :])
newsboys.predict(newsgroups_vectorized_test.data)
rfc.predict(newsgroups_vectorized_test.data)

We can actually ALSO get **probability predictions from these sklearn models, too, as follows.

clf.predict_proba(cancer_df.iloc[testing_indices, :])
newsboys.predict_proba(newsgroups_vectorized_test.data)
rfc.predict_proba(newsgroups_vectorized_test.data)

ROC curves

We have previously seen confusion matrices which are based on the classes of TP, TN, FP, and FN. But what constitutes a "positive" versus a "negative" prediction? Since binary classification predicts 0's and 1's (or negatives and positives), and since the output of binary classification models (such as Logistic Regression, Binary Classification Decision Trees, and Binary Classification Random Forests) are probabilities, it's very natural to predict 0 if the probability is less than 0.5 and to predict 1 if the probability is greater than 0.5. But this threshold is arbitrary. Here's a question. How does the sensitivity and specificity of a prediction change if we change the threshold?

If we increase the threshold then we'll make fewer positive* predictions so sensitivity must decrease and specificity must increase
If we decrease the threshold then we'll make more positive* predictions so sensitivity must increase and specificity must decrease

Here's how this effect looks if we predict the 16th news article genre in the data we've most recently considered. Hover over the curve to see how the sensitivity and specificity change as a function of the threshold. And remember, the threshold is what determines if the model chooses to predict a 0 or 1. If the probability prediction is greater than the threshold then the model predicts a 1, otherwise it predicts a 0.

from sklearn.metrics import roc_curve, roc_auc_score

# fpr: 1-specificity
# tpr: sensitivity
fpr, tpr, thresholds = roc_curve((newsgroups_vectorized_test.target==15).astype(int), 
                                 rfc.predict_proba(newsgroups_vectorized_test.data)[:,15])
roc_df = pd.DataFrame({'False Positive Rate': fpr, 'True Positive Rate': tpr,
                       'Threshold': thresholds})
# Compute AUC score
auc_score = roc_auc_score((newsgroups_vectorized_test.target==15).astype(int), 
                          rfc.predict_proba(newsgroups_vectorized_test.data)[:,15])

fig = px.area(roc_df, x='False Positive Rate', y='True Positive Rate',
              title=f"ROC Curve (AUC = {auc_score:.2f})",
              labels={'False Positive Rate': 'One minus Specificity', 
              'True Positive Rate': 'Sensitivity'},
              hover_data={'Threshold': ':.3f'})

# Add diagonal line (random model)
fig.add_shape(type='line', x0=0, y0=0, x1=1, y1=1, 
              line=dict(dash='dash', color='gray'))

fig.update_layout(title_x=0.5)  # Center the title
fig.show()

Partial Dependency Plots

Even though many Machine Learning models don't have linear forms and they make their predictions in other "algorithmic" ways, we can still see the relationship between outcomes and predictor variables through so-called Partial Dependency Plots. Here are examples for the news dataset that we've been demonstrating things with.

from sklearn.inspection import PartialDependenceDisplay
# https://scikit-learn.org/stable/modules/partial_dependence.html#pdps-for-multi-class-classification
X = newsgroups_vectorized_test.data.toarray()[np.random.choice(np.arange(7532,dtype=int), size=100, replace=False),:]
x = 89362  # np.argmin((newsgroups_vectorized_test.data.toarray()==0).sum(axis=0))
           # np.argmax(rfc.feature_importances_)
#px.scatter(pd.DataFrame({'fi': rfc.feature_importances_,
#                         '!0': (newsgroups_vectorized_test.data.toarray()!=0).sum(axis=0),
#                         'ix': np.arange(len(rfc.feature_importances_))}),
#           x='fi', y='!0', hover_data={'ix': ':.1f'})
    
X = X[X[:,x]!=0, :]

fig,ax = plt.subplots(4,5, figsize=(12,8))
ax = ax.flatten()
for i in range(20):
    PartialDependenceDisplay.from_estimator(rfc, X, (x,), target=i, ax=ax[i])

fig.tight_layout()
plt.show()