Algorithm - ovidiopr/tmmnlay GitHub Wiki

For the implementation of the Transfer-Matrix Method in tmmnlay I have followed the notation described here:

1. L.A.A. Pettersson, L.S. Roman, and O. Inganäs, "Modeling photocurrent action spectra of photovoltaic devices based on organic thin films," J. Appl. Phys. 86, 487-496 (1999).

Several techniques are possible in order to obtain the reflection and transmission coefficients of the electromagnetic field in multilayered structures, but probably the most elegant approaches is to employ the transfer-matrix method. Multilayer structures with isotropic and homogeneous media and parallel-plane interfaces can be described by 2×2 matrices due to the fact that the equations governing the propagation of the electric field are linear and that the tangential component of the electric field is continuous [1,2]. Consider a plane wave incident from left at a general multilayer structure having m layers between a semi-infinite transparent ambient and a semi-infinite substrate, as schematically described in Fig. 1. Each layer j ( j = 1, 2, …, m ) has a thickness d_j and its optical properties are described by its complex index of refraction n_j = n_j + i k_j (or, alternatively, by the complex dielectric function ε = ε'_j + i ε"_j), which is a function of the wavelength (energy) of the incident light.

The optical electric field at any point in the system can be resolved into two components corresponding to the resultant total electric field; one component propagating in the positive x direction and one in the negative x direction, which at a position x in layer j are denoted E₀⁺(x) and E₀^-(x), respectively. An interface matrix (matrix of refraction) then describes each interface in the structure:

	(1)

where t_jk and r_jk are the Fresnel complex transmission and reflection coefficients at interface jk. For light with the electric field perpendicular to the plane of incidence (s-polarized or TE waves) the Fresnel complex reflection and transmission coefficients are defined by:

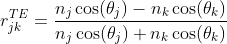	(2a)

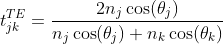	(2b)

and for light with the electric field parallel to the plane of incidence (p-polarized or TM waves) as:

	(3a)

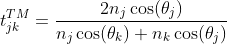	(3b)

being cos(θ_j) = (1 - n₀² sin²(θ₀)/n_j² )^1/2, n₀ the refractive index of the transparent ambient, θ₀ the angle of incidence, and θ_j the angle of refraction in the layer j. The layer matrix (phase matrix) describing the propagation through layer j can be written as:

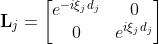	(4)

where ξ_j = 2πn_j cos(θ_j)/λ, λ is the wavelength of light in vacuum and β_j = ξ_j d_j is the phase factor of layer j, which represents the phase change experienced by the wave as it traverses the layer. Now, by using the interface matrix and the layer matrix described in Eqs. (1) and (4), we can obtain the total system transfer matrix (scattering matrix) S, which relates the electric field at ambient side and substrate side by:

	(5)

and S can be written as:

	(6)

When light is incident from the ambient side in the positive x direction there is no wave propagating in the negative x direction inside the substrate, which means that E^-_m+1 = 0. For the total layered structure the resulting complex reflection and transmission coefficients can be expressed by using the matrix elements of the total system transfer matrix of Eq. (6) as:

	(7a)

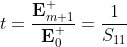	(7b)

Equation (7) is valid for both, TE and TM, polarizations and the total transmittance and reflectance can be calculated as r = (r^TE + r^TM)/2 and t = (t^TE + t^TM)/2, respectively. Now, in order to calculate the internal electric field in layer j, the layer system can be divided into two subsets, separated by layer j, which means that the total system transfer matrix can be written as:

	(8)

1. R.M.A. Azzam and N.M. Bashara, Ellipsometry and Polarized Light (North Holland, 1977).
2. A. Richter and J. Sturm, "Dielectric and optical properties of C₆₀ material studied by ellipsometry and quantitative IR and UV/VIS spectroscopy," Appl. Phys. A 61, 163-170 (1995).