猛獣を飼いならす - 数学はここから始めよう

導入

数学を怖がる人は多いようです。数字のことやそれで何をするかを考えると怖気づく傾向がある場合、このモジュールはあなたのためのものです。数字を数えたり、足したり、割ったりして、猛獣を飼いならすのにどれだけのことができるかお見せしましょう。

私たちが取り組む一般的な問題

データを扱うとき、私たちはここで学ぶ方法で対処するいくつかの一般的な問題に出くわします。

「正常」とは？ 何が違う/特別なのでしょうか？ 2つの異なる実体（例えば国）をどのように比較すれば良いのでしょうか？

私は何を扱うのですか？

データ内の複数の値を操作するとき、あなたが得ることができる情報の重要なポイントの一つは、データがどのように分散しているか、ということです。これは、あなたが何を扱っているかを把握するのに役立ちます。

範囲

あなたが最初に知りたい事はデータの範囲、つまりあなたのデータはどこからどこまで広がっているか、ということでしょうか？小さな数字から始まっていますか？大きな数字？マイナスからプラスまでありますか？こういったことは、データを取り扱うために役立つ重要な情報です。

範囲を見ると、データのエラーを見つけるのにも役立ちます。例えばあなたが、背の高さを比較してセンチメートルで、そのサイズを入力するように人々にお願いしたとしましょう​​。あなたは例えば、データの値が127から622までの範囲であることを見つけたとしましょう。そこには明らかに間違いがありま​​す。身長6メートルの人は非常にまれであり、あなたがそのひとりを捕まえられる可能性は比較的小さいです。あなたは、データに立ち戻ってチェックする必要があります。

範囲を見つけるにはどうしたら良いでしょうか？単純にデータをひと通り見て、最小値と最大値、最低と最高を見つけます。スプレッドシートでは、=MINと=MAXという数式でこれを行うことができます 。

それでは次のデータがあるとしましょう​​（身体の大きさを取り出してみましょう）

163.1 162.2 210.5 201.0 188.7 182.6 153.0 173.5 146.6 148.0

質問：あなたのデータセットの範囲はどこからどこまでですか？

ヒント ：最低数（最小値）と最高数（最大値）を見つけます。回答：範囲は146.6 から210.5 です

いくつありますか？

自問できる次の重要な質問です：いくつありますか？例えば、何人調査しましたか？どれだけの国のことを知っていますか？などです。これは単純に見えるかもしれませんが、統計にとって非常に重要です。

私たちはそれをどのようにして得るのでしょうか？単純に数える！スプレッドシートでは、これは=COUNTまたは=COUNTA という数式になります。

以下のデータで、私たちはいくつデータポイントを持っていますか？

163.1 162.2 210.5 201.0 188.7 182.6 153.0 173.5 146.6 148.0

10です！簡単ですよね？単純に数えて範囲を見ることで、私たちはすでに貴重な情報を持っています！それでは、もっと調べてみましょう。

分布

次にあなたが見てみたいのは、データがどのように分布しているかです。これは、一般的に、ヒストグラムと呼ばれるプロットを用いて行われます。ヒストグラムは、単純にそれぞれの値が出現し、そこから進行する頻度をカウントします。

それで私たちはこれをどのようにして行うのでしょうか？これは、一般に、データをビニングすることによって行われます。これはどういう意味でしょうか？基本的に、私たちが着目する番号の範囲であるビンを作成します。

上記で使用したデータでこれをやってみましょう。データの範囲は、146.6 から210.5 までです。妥当なビンを作成しましょう。例えば140-160、160-180、180-200、そして200-210 を使いましょう​​。そして数えて行きます。140と160の間にはいくつ値がありますか？160 から180 の間にはいくつ？等々。

結果：

ビン	個数
140-160	3
160-180	3
180-200	2
200-220	2
素晴らしい。これを単純なグラフィックとして描画してみましょう。

連番	ビン	個数
1	140-160：	***
2	160-180：	***
3	180-200：	**
4	200-220：	**

これがヒストグラムに存在するすべてで、データがどのように分布しているかを示しています。

値が10個だけでは、これはあまり多くのことを教えてくれませんが、数がもっと多いと、これは超便利です。

知りたいこと：どれだけのピークがあるか？ピークはひとつ、または複数？（複数のピークがあるう場合、何かしら異なるグループが存在することを示している場合があります。）これは明確なピークがあり両側が均等に（下記のように）分布している_正規分布_ですか？

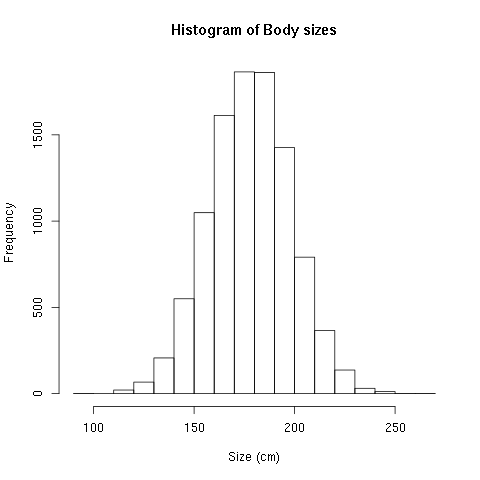
あるいは分布には「歪み」（すなわち、左にピークがあり右にロングテールがある）がありますか？

分布を見ると、さらにどのような記述子を使ったら良いかが分かります。

正規とは何か？

よくある次の質問は「正規」とは何かということです。その意味するところは、どうしたら私は何かを見て価値があるかどうかを見分けることができますか、ということです。（何が特別かについては以下で把握します。）

これを見つけるためにさまざまな方法があります。

平均

「正規」であるものを見出すのに最もよく使われる方法は平均（または「アベレージ」）です。「平均年収」が増えているとか減っているとかいうニュース記事を目にすることがあると思います。しかし、それはどのようにして計算するのでしょうか？とてもシンプルです。すべての数字を合計し、その結果をその数字の数で割り算します。

例：1、2、3、4の平均 =（1 + 2 + 3 + 4）/ 4 = 10/4 = 2.5

以前使った高さの平均値を計算することはできますか？

163.1 162.2 210.5 201.0 188.7 182.6 153.0 173.5 146.6 148.0

回答：平均値は172.92です。

あなたのデータが正規分布している場合、平均は素晴らしいツールです。その場合には、どこが分布の最大値かとか、それゆえ何が正規かに気づく、といったことについて多くのことを教えてくれます。

中央値

別の例を見てみましょう。全国の所得分布を見てみると、分布は正規ではありません。それは次のように見えます。

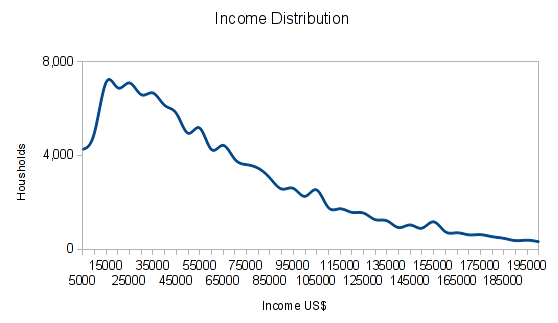
さて、平均所得を眺めると、それはかなりの数字に見えるかもしれません。しかしあなたの収入が平均を下回っていても、人口の大半がその収入はわずかしか無いという単純な理由で、その収入は人口の半分以上を上回っています。中央値は、私たちにこれを教えてくれます。中央値を計算するには、単に持っているデータを並べ替えて、ちょうど中央にある値を選びます。

それでは、次のデータの中央値を計算してみましょう：

162.0 159.1 169.9 191.3 195.9 139.8 186.0

まず、データを並べ替えます（昇順、降順は関係ありません）

139.8 159.1 162.0 169.9 186.0 191.3 195.9

そして、ちょうど中央の値を選択します：169.9 - これが中央値です！

値が偶数の場合はどうなりますか？単純にちょうど真ん中の2つの値の平均をとります。

次の中央値を計算してみてください。

163.1 162.2 210.5 201.0 188.7 182.6 153.0 173.5 146.6 148.0

結果：168.3、163.1と173.5の平均

モード（最頻値）

平均値、中央値のいずれもが私たちが本当に知りたいことを教えてくれないことがあります。兄弟の数を尋ねた調査を見てみましょう。回答は次の通り：

0, 1, 1, 1, 1, 2, 2, 2, 3, 5

兄弟数の平均は1.8、中央値は1.5です。しかし、私たちが本当に知りたいのは何人兄弟がいちばん多いのか、ということです。そこで、数えてみます。

0 - 1 1 - 4 2 - 3 3 - 1 5 - 1

1が最も多い答えだということが分かります。これがモード（最頻値）です。

データが離散的でない場合はどうしたら良いでしょうか？上述のようにビンを作成して数えます。

時には、期待通りの結果が得られないこともあります。同じ件数の2つの異なる値があるかもしれません。それが明確に分かれているケースでは、これをバイモーダル（双峰）分布（3つ以上のケースではマルチモーダル）と呼びます。

データのばらつきの大きさは？

次に知りたいのは、データのばらつきの大きさです。便利な2つの指標：標準偏差と中央値絶対偏差。標準偏差は平均値をもとに算出し、とてもよく使われるものです。中央絶対偏差の使用頻度はやや落ちますが、すでに中央値を使用している場合に使うのがベストでしょう。

標準偏差

それでは、まず最初に標準偏差を見てみましょう。これは平均して、データポイントがどのくらい平均値から離れているかを教えてくれます。その値と平均の差異の二乗を合計し、その合計を測定値の数から1を引いたもので割り、さらにその平方根を取ります。集中力はまだ大丈夫ですか？

もっと重要なこと：正規分布の場合 - データポイントの68.27パーセントは平均からの1標準偏差内に入り、そして95.45パーセントは平均から2標準偏差内に入ります。ですから、データの大半がどこにあるかが分かると良いアイデアが生まれます。憶えにくい場合はこのイラストがうまく表現しています。

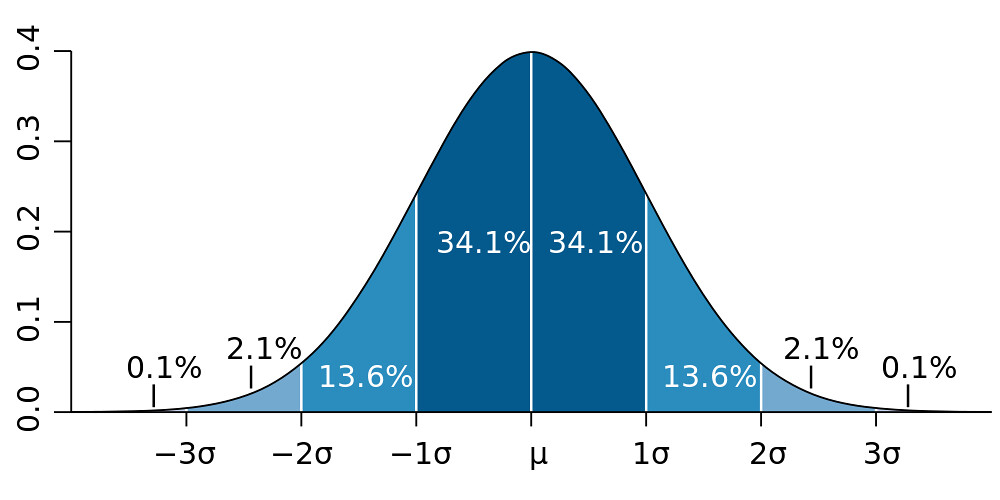
画像CC-BY ウィキペディアメンバーMwtoews

複雑に聞こえますね。やってみましょう。

それでは、上のデータを見てみましょう：1、2、3、4 です。

私たちはすでに平均が2.5であることを知っています。

それでは、標準偏差を計算してみましょう：

値	平均との差	平方差
1	-1.5	2.25
2	-0.5	0.25
3	0.5	0.25
4	1.5	2.25
さあ、差の二乗を合計してみます：それは5です。

データポイントの数マイナス1で5を割ります。

5/(4-1)

すなわち5/3です。

そして、その平方根を取ります。

これで、1.291にたどり着きました。 - これは、測定値の68.27パーセントは、平均からこの距離に入ることを意味します（正規分布だと仮定）。

ややこしそうですね！確かに少し。でも加算、乗算、そして除算だけだということを覚えておいてください。魔法めいたものは使っていません。幸いなことに、これが必要な場合、スプレッドシートにはこのための式があります： =STDEV 。

中央絶対偏差

前述の通り、標準偏差は平均をベースにしているので、平均値を使用できる場合にうまく動作します。しかし、中央値を使用する場合はどうでしょうか？中央絶対偏差を使用してください。これは同じように動作しますが、もっと簡単です：中央値と、各値と中央値の差の絶対値を計算します。その後、差の中央値を計算します。

たとえば、次のようなデータがある場合

1, 2, 3, 4, 5

中央値は3です。

差分は次のとおり： 2 1 0 1 2 - 並べ替えると、0 1 1 2 2。

中央絶対偏差は：1。

右、実現可能なサウンド？

データを正規化 - 別名：物事の比較

私たちが話題にしていることについて何かアイデアがある場合には、物事を比較する方法を考えてみましょう。

たとえば、いくつかの点で全く異なる二つの国を比較するとしましょう​​。例えばそのGDPを比較しようと思えばできますが、何も有益なことを教えてはくれません。例えば、ある国が非常に大きく別の国が非常に小さい場合は、大きい方が、より高いGDPを有することになります。これは、より生産的だということになるのでしょうか？いいえ。私たちは、対等な立場でそれらを比較する必要があります。通常、これには国の規模が分かるものが使われます。それは多くの場合、人口です。

生産性を比較するために、GDPを人口で割り算します。これは、正規化と呼ばれています。これで私たちは、一人当たりのGDPを比較することができます。この比較はよく行われるので、あなたはおそらく、この指標を聞いたことがあるでしょう。

値を正規化するもうひとつのやり方は、パーセンテージを使用することです。たとえば、どの国が健康な生活を送れているのか比較する場合、GDPで正規化するのはとても良いやり方です（たとえばある国は比較的多数が健康に暮らしているが、こちらの国はそうではないとか）。または選挙を考えてみると、しょっちゅうパーセンテージに出くわすということがおわかり頂けると思います（例えば、私たちは何人が政党Aに投票したか計算し、それを有効投票数で割ったりします）。

何が特別かを見つける - Z-スコア

Zまたは標準スコアは、何が特別かを把握するための良い方法です。例えば、あなたが選挙結果を持っていて、レポートに値する興味深い場所を見つけたいとしましょう​​。あなたができることのひとつは、政党が非常によく行っている場所を把握することです。Z-スコアは、この用途に最適です。

測定値のZスコアは次のように計算されます

（X - 平均値）/標準偏差。

Zスコアでは、平均値からの標準偏差における値の距離を得られます。これで、任意の制限を設定して、次のように言うことができます：投票のZスコアが2以上の場所は興味深い。なぜならこれは例外的に多くの人々が特定の政党に投票したことを意味するからです。-2以下のZスコアも興味深いです。なぜなら例外的に少数の人々しか投票していないためです。郡や地域のZスコアを見ることで、これをより細分化することができます（多くの場合、そこには地域差などがあります）。憶えておいてください - （普段distrubutedデータを持っている場合）測定値の95.45パーセントは、平均から2標準偏差に落ちます。その意味するところは次のようなものです：Zスコアには5パーセント未満の変化があり、2. 5％以上（または以下）になると、かなり目立ちます。 不十分です：標準偏差が3の場合、あなたのチャンスは1%未満です（得票の99.73パーセントは正規分布で平均値から3標準偏差内にあります）。

全体的に、Z-スコアは、データ値が異なるものを描き出すための道具箱の便利な付加機能です。

ふりかえり

このモジュールでは、定量的なデータを理解するのに必要な基本的な数学について話しました。そして、あなたが扱っている対象（一般的に記述統計と呼ばれています）は何かを把握する方法について話しました。私たちは私たちはオレンジにリンゴを比較することができる方法を（必要な場合）明らかにしてきました。そして最終的に何かについてどういうところが特別なのかを把握することができるように、Z-スコアを詳しく見てきました。

基礎数学クイズ

1.正規分布に関して、次のうち正しいのはどれですか

(1)70% of values are within one standard deviation from the mean (2)50% of values are within one standard deviation (3)Plotting out a histogram one would see two peaks (4)None of the other answers

2.Assuming a normal distribution what is the likelihood a point with a Z-Score of 2

(1)25% (2)10% (3)50% (4)<5%

3.What is the mean of the following values: 10, 12, 6, 17

(1)10 (2)11.25 (3)11 (4)17

4.If you have a median of 50, how many values will be less than 50?

(1)10% (2)25% (3)Depends on the distribution (4)50%