AI 기초

by 서울대학교 장병탁 교수님

AI란?

• Thinking Humanly: Cognitive modeling approach, build human-level general intelligence
• Thinking Rationally: Laws of thought approach, thinks right, normative than descriptive(deriving correct conclusions)
• Acting Humanly: Turing test approach, behave intelligently like humans
  NLP, Knowledge representation, Automated reasoning, Machine Learning
• Acting Rationally: Rational agent approach, behaves rationally or does the right thing
  achieve best expected outcome, maximize goal achievement

※ Rational Agent: entity that perceives and acts, 인간처럼 인식하지는 않더라고 best performance를 산출하는 agent를 만드는 것

• Intelligent(rationality) Agents: choose action that maximizes the performance
• Problem-Solving Agents: problems / solutions / search algorithms
• Knowledge-Based Agents: deduce actions from the knowledge, represent knowledge using logic(명제, first-order logic)

---

Information Theory

• Information: x를 관측함으로 인해 얻게 되는 정보량, 확률이 낮은 사건일 수록 얻는 정보량이 많다.
  
• Entropy: 문제의 불확실성을 나타냄
  
• Mutual Information:
  
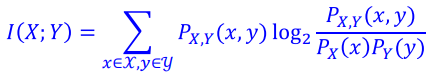
• Relative entropy(KL Divergence):
  

---

Temporal Reasoning

intepret the present, understand the past, predict the future

Inference in Temporal Models

• Filtering: 과거 evidence를 통해서 현재의 상태를 estimation / P(X_t|e_1:t)
• Prediction: 과거 evidence를 통해서 미래의 상태를 estimation / P(X_t+k|e_1:t)
• Smoothing: 과거의 상태를 더 잘 estimate(essential for learning) / P(X_k|e_1:t)
• Most likely explanation: 가장 그럴듯한 path를 찾는 것 / argmax_X_1:t{P(X_1:t|e_1:t)}

---

Probabilistic Reasoning

Bayesian network

Directed acyclic graph(DAG) representing a full joint probability distribution of random variables

※ Approximate Inference for Bayesian Networks

• Draw N samples from a sampling distribution
• Compute an approximate posterior probability
• Show this converges to the true probability

■ Methods

Direct sampling
Rejection sampling
Likelihood weighting
Markov chain Monte Carlo(MCMC)

---

Utility-Based Agents

Markov Decision Process(MDP)

Sequential decision problem for fully observable, stochastic environment with a Markovian transition model and additive rewards
ex: 바둑, 로봇 움직임 등

• states / actions / transition model / reward function
• policy: action을 선택하는 solution, optimal policy(highest expected utility)를 찾는 문제
• Bellman Equation으로 optimal policy 구함

※ POMDP: Partially Observable MDP

---

Advanced ML

by 서울대학교 최진영 교수님

Linear Regression

Regression: a process that finds a parametric model f_hat that gives the best fit of f for the observed samples

y_i = f_hat(x_i) + ε_i
ε_i -> iid, zero mean, variance σ^2

MLE(Maximum Likelihood Estimation): 정규분포 내에서 잔차(ε_i)가 나타날 확률의 곱(i=`..n)이 가장 크도록 하는 θ를 구하는 것
= LSE 문제와 같음(ε_i이 0에 가까울수록 확률곱은 커지고, Least square가 작아지므로)

Bias(underfitting) and Variance(overfitting)

Bias: 추정치 평균과 실제값 평균의 차이가 크다 -> underfitting(training error)
Variance: 관측 sample에 따라서 추정치 estimation의 변화가 크다 -> overfitting(validation error)

변수의 개수가 많으면 overfitting, 적으면 underfitting
-> 변수의 개수를 늘려가면서 validation error가 커지는 시점을 택하거나, PCA, regularization 사용

Regularization

• Ridge: L2-norm
• Lasso: L1-norm
• Elastic: Ridge + Lasso

---

Nonlinear Regression

• High-order polynomial linear model
• Sine/cosine basis linear model
• Radial basis linear model: 특정 포인트(center)들과의 거리를 사용한 변수의 선형 결합
• Piecewise linear model: 구간 별 linear regression의 결합
• Neural network model

Evaluation Metrics

Precision & Recall

Precision(=sensitivity): TP/(TP+FP), Recall: TP/(TP+FN) Specificity: TN/(TN+FP)

ROC(Receiver Operating Characteristic) curve / AUC(Area Under curve)

x축: 100 - specificity y축: sensitivity

Acurracy

(TP + TN)/all

F1 score

2 * Precision*Recall / (Precision + Recall)

---

Gaussian Process Regression

regression 함수 f에 gaussian 분포의 perturbation을 가해 존재할 수 있는 여러 곡선을 구하는 것
각 x에 대해서 y를 gaussian 분포로 제시
λ를 조절하면서 uncertainty의 정도를 조절한다.
λ가 작으면 관측값이 주변에 영향을 미치지 못해서 uncertainty가 커지고, 크면 너무 많이 미쳐서 underfit이 되어버림
참고

---

Bayesian Framework

AI: 학습(Learning/Training)과 추론(inference)으로 이루어짐
추론: P(A|B)[Posteriori Probability]
학습: P(B|A)[Likelihood Probability] * P(A)[Priori Probability]

Information (Theory)

• 정보량(=surprise =uncertainty): 얼마나 알고 있는 지가 아니라 해당 사건으로 인한 정보의 가치를 나타냄, 일어날 확률이 적은 사건일수록 가진 정보량이 큼.
• Entropy: average amount of information, E[I(X)] = -E[log(p_k)] = -∑p_k*log(p_k)
  확실한 사건에 대해서는 entropy가 0에 가까우므로 학습할 필요가 적음.

KL Divergence

q_k(x;W): k가지 class에 대한 output probability
p_k(x): 정답 probability
q_k를 p_k에 가깝도록 학습시키는 것이 목표

Mutual Information: Output Y의 관측에 의해 알 수 있는 X의 uncertainty

X와 Y가 independent하다면 I(X;Y) = 0

Conidtional Entropy(Y가 관측되었을 때의 X의 entropy): H(X|Y) = H(X, Y)-H(Y)
Joint Entropy: H(X, Y)

---

Bayesian Learning

Bayesian Therom을 이용해 데이터 set D로부터 θ의 분포를 추정하는 것, p(θ|D)

Nonparametric Density Estimation

in practice, unimodal하지 않은 density function으로서 존재하는 경우가 많음(multimodal density)
nonparametric density estimation을 위한 다양한 방법이 있음

• Histogram: x축을 잘게 나누어서 해당 bin에 존재하는 데이터의 갯수로 분포를 표현(p = k/nV)
  V를 고정한 상태에서 k의 변화가 density를 추정함.
• KNN: 특정 데이터 x에서 근접한 k개의 데이터를 포함할 때까지 V를 키워가는 방법 k를 고정한 상태에서 V의 변화가 density를 추정함(V가 크다는 것은 density가 낮음을 말함).
• Parzen Windows: uniform distribution(1/h for x-h/2 ~ x+h/2)이 커널인 KDE
  histogram과 마찬가지로 V(h^d)를 고정한 상태에서 k의 변화(커널함수의 합)으로 density 추정
• GMM(Gaussian Mixture Model): x가 여러 개의 Gaussian 분포 중 어느 분포에 속할 확률이 높은지로 density 추정
  
  EM(Expectation-Maximization)을 이용해서 최적 파라미터들을 찾는다.
• MH(Metropolis Hastings): 임의의 proposal distibution이 주어졌을 때, p(x)에 대한 MCMC 샘플링을 하는 알고리즘
  proposal distribution Q(x'|x)을 통해 이전 샘플링(x)을 참고하여 다음 샘플링(x')을 예측
  acceptance probability 를 이용해서 다음 샘플을 기각할지 받아들일지 결정
• Gibbs Sampling: 다른 모든 변수는 고정하고 한 변수씩 샘플링해 나가 새로운 Markov Chain을 형성하는 MCMC의 한 방법​
  새롭게 형성된 Markov Chain을 통해서 sample을 얻는다
  참고

■ MCMC(Markov Chain Monte Carlo) 참고
샘플링 알고리즘으로, 높은 차원의 문제를 빠른 수렴 속도로 해결 가능
stationary distribution이 target distribution p(x)가 되도록 Markov Chain을 설정하는 것
바로 이전 샘플만 다음 샘플의 추출에 영향을 주는데도 확률 분포를 거의 정확히 모방함

※ Markov Chain
한 상태 x_i에서 x_j로 이동할 조건부 확률분포[T(X_j|x_i)]가 주어져 있음
상태 사이를 충분히 많은 횟수 이동하게 되면 각 상태의 방문횟수의 비율이 특정 확률분포(stationary distribution)로 수렴