Stat: Sets - mrprov12/DSPrep GitHub Wiki

Event:

In probability theory, an event is an outcome or defined collection of outcomes of a random experiment. Typically, events are represented with a capital letter from the beginning of the alphabet, though there are some exceptions to this, such as the sample space as defined below.

Event A, where the coin lands on tails:

A={T} Event B, where the coin lands on heads:

B={H} Event C, where the coin lands on either heads or tails:

C={H, T}

Random Experiment:

A random experiment is an experiment or a process for which the outcome cannot be predicted with certainty.

Certain or Impossible:

If a specific outcome is guaranteed (for example, if both sides of a coin are heads, the outcome is guaranteed to be heads), then we refer to the outcome as certain. Lastly, if a specific outcome can never occur (as getting a tails on the aforementioned coin flip), the outcome is formally referred to as impossible.

Set:

A set in mathematics is simply a collection of well defined and distinct objects, and is also an object in its own right. Notice that in each and every set mentioned above, there are not any duplicates. This is one of the most important properties of a set, that each object is distinct, that is, no object can be represented more than one time in a set.

Sample Space:

If the outcome of a random experiment is unknown, but all of the possible outcomes are predictable in nature, then the set of all possible outcomes is known as the sample space and is denoted S. S represents every possible outcome of a random experiment; see an example below: S={H, T}

Set Union

A∪B

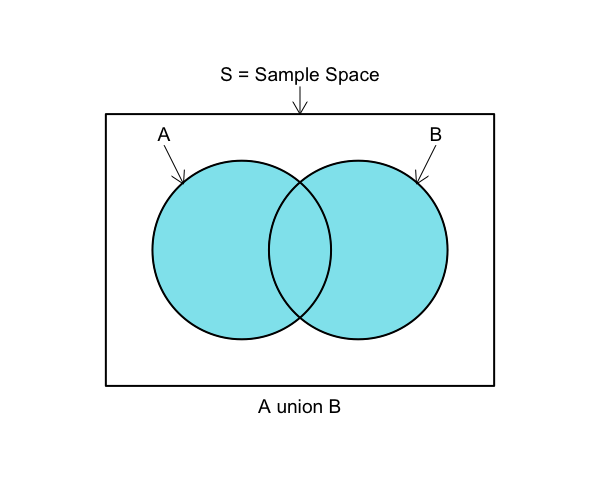
Step 1: Clearly define the two events

A={1,3,5}
B={1,2,3,4}

Step 2: Find the union of the two events

A∪B={1,2,3,4,5}

Solution
A∪B={1,2,3,4,5}

Union of more than 2 events

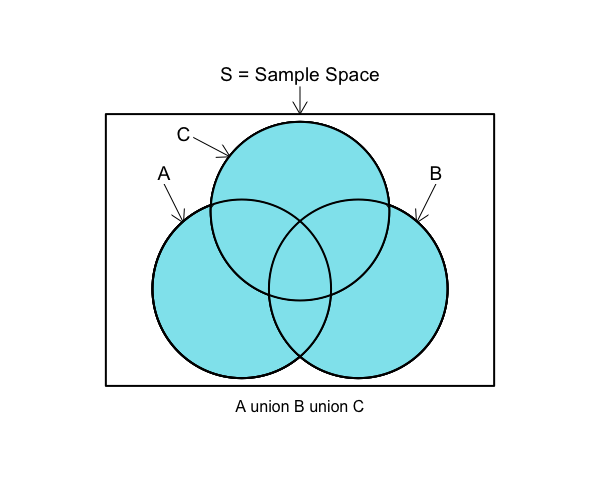
Step 1: Define the subset of outcomes for each event
A={333}
B={444}
C={555}
Step 2: Define the union of the three events
A∪B∪C={333,444,555}
Solution
A∪B∪C={333,444,555}

finding union with python

def list_union(lst1, lst2):
    # Make a new list, to avoid mutating a parameter
    new_lst = lst2.copy()

    # Iterate through lst
    for obj in lst1:
        # If the object doesn't already exist in lst2
        if obj not in lst2:
            # Then add it to the new list
            new_lst.append(obj)

    new_lst.sort()

    return new_lst

# Define two sets
set1 = {1, 3, 5, 7}
set2 = {2, 4, 6, 8, 1}

# Execute the union, and save the result to a new variable
new_set = set1.union(set2)

# Will print:
# {1, 2, 3, 4, 5, 6, 7, 8}
print(new_set)

Intersection

AB or A∩B

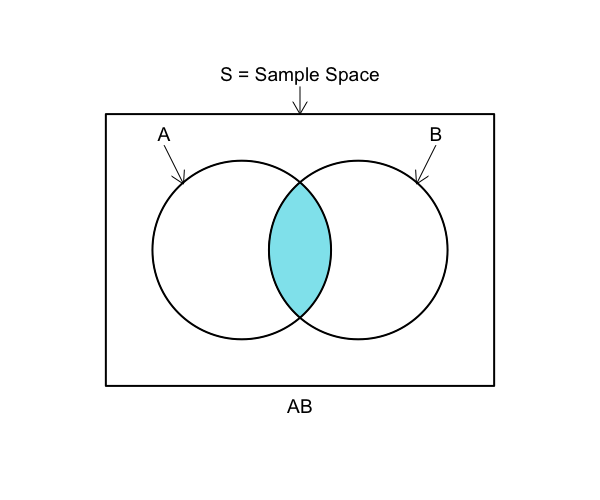
Find the intersection of the two events, A and B:

A={1,2,3,4,5,6} and B={2,3,4}
Step 1: Define the two events
A={1,2,3,4,5,6}
B={2,3,4}
Step 2: Find the intersection (all values in both sets)
A∩B=AB={2,3,4}
Solution
A∩B=AB={2,3,4}

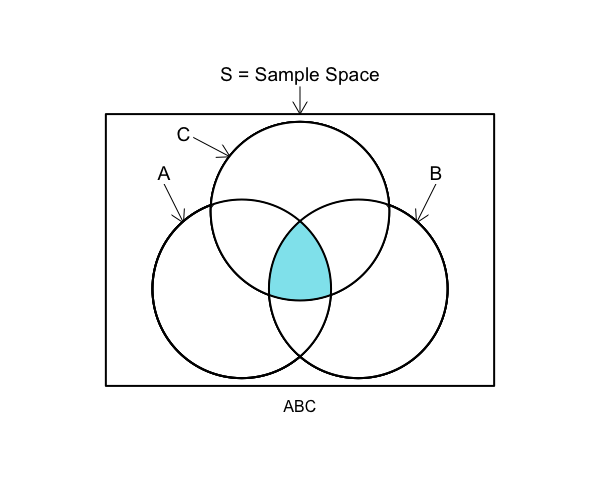
Step 1: Define each event as a set

A={1,2,3}
B={3,4,5,6}
C={1,3,5}

Step 2: Find the intersection

A∩B∩C=ABC={3}

Absorption

A∪(A∩B)=A

Finding the intersection using python

def find_intersection(lst1, lst2):
    # Declare a new list to populate and return
    new_lst = []

    # Iterate through lst1
    for obj in lst1:
        # if that object is also in lst2, then add it to the new list
        if obj in lst2:
            new_lst.append(obj)

    # Sort the list before returning it
    new_lst.sort()

    return new_lst

# Declare two lists
lst1 = [1, 1, 1, 1, 2, 3, 4, 5, 5, 6, 7, 8, 9]
lst2 = list(range(5, 12))

# Use the set() function to parse the lists into sets, this will eliminate
# duplicated objects in the list
set1 = set(lst1)
set2 = set(lst2)

# Find the intersection and assign it to a new variable
my_intersection = set1.intersection(set2)

# Will print:
# {5, 6, 7, 8, 9}
print(my_intersection)

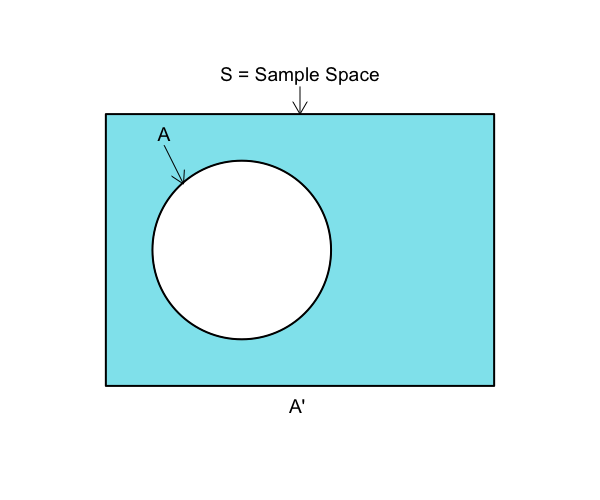
compliment of a set

complement(A) = A^c = A^0 = A^⎯⎯⎯⎯ = A′

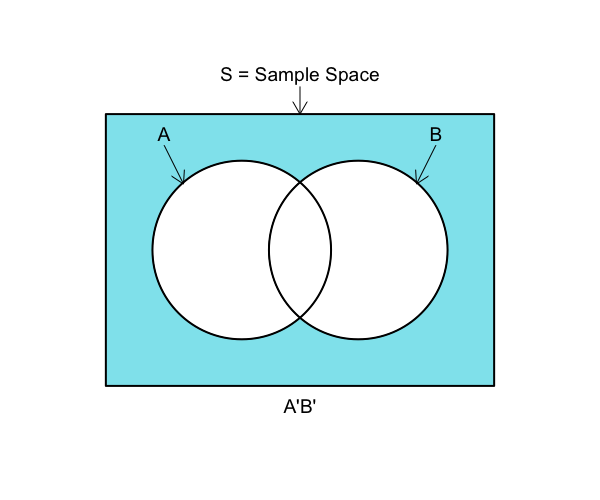
A^cB^c = {1,2,5,6}

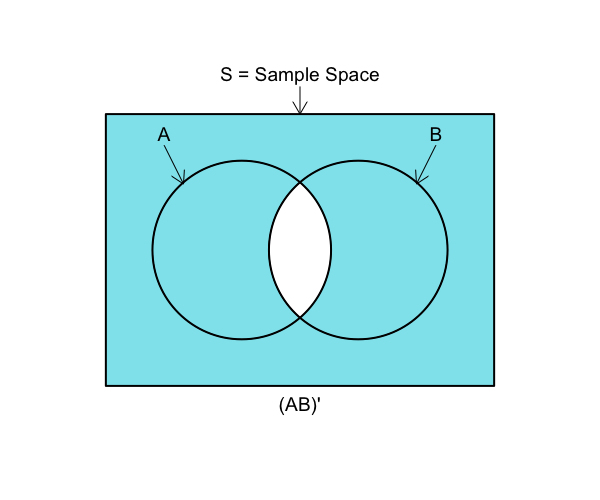
(AB)^c

Definition: Complement of a Set In set theory, the complement of a set, A, refers to all elements not in A. When all sets under consideration are considered to be subsets of a given sample set S, the absolute complement of A is the set of elements in S but not in A.

Step 1: Define the sample space and the event

S={1, 2, 3, 4, 5, 6}
A={2,4,6}

Step 2: Find the complement of A
Ac={1,3,5}

Solution
Ac={1,3,5}

def find_complement(event, sample):
    # Declare a new list to collect and return
    new_list = []

    # Iterate through the sample space
    for obj in sample:
        # If the object isn't in the event
        if obj not in event:
            # Add it to the new list
            new_list.append(obj)

    # Sort and return the list
    new_list.sort()

    return new_list

the difference of two sets

A−B = AB^c

A−BC = A(BC)^c

sample −event

def find_complement(event, sample):
    # Convert the lists to sets
    event_set, sample_set = set(event), set(sample)

    # Find the difference between the two sets
    diff = sample_set.difference(event_set)

    # Return the new set
    return diff

Laws of Set Algebra

Commutative

Just like addition and multiplication, both union (∪) and intersection (∩) are commutative. That is to say that:

A∪B=B∪A AB=BA

Associative

Again, like addition and multiplication, both union (∪) and intersection (∩) are associative. That is to say that:

(A∪B)∪C=A∪(B∪C)=A∪B∪C (AB)C=A(BC)=ABC

Distributive

Lastly, like addition and multiplication, both union (∪) and intersection (∩) are distributive. That is to say that:

A∪(BC)=(A∪B)(A∪C) A(B∪C)=(AB)∪(AC) In addition to these fundamental laws, there are other common laws and properties of sets, unions, and intersections

Idempotent Laws

There are two idempotent laws of sets which might seem self-explanatory, but they should be explicitly stated.

A∪A=A A∩A=A

Domination Laws

The domination laws refer to both the universal set, as well as the null set. The universal set, is a set which contains all objects or elements and of which all other sets are subsets. A universal set that has already been referenced in this course is the sample space of a random experiment. The null set is what you may imagine it to be, and is also often called the empty set; this is a set which does not contain anything.

Notation:

U= Universal Set ∅= Null Set The two domination laws are shown below:

A∪U=U A∩∅=∅

Absorption Laws

There are two absorption laws, as listed below:

A∪(AB)=A A(A∪B)=A

Identity Property

A set has the indentity property under a particular operation if there is an element of that set that leaves every other element of the set unchanged under a given operation. See a generalized example below:

A∪∅=∅∪A=A

Complement Laws for the Universal and Null Sets

The complement of either the null set or the universal set can also be found, but it can seem slightly less intuitive than a typical complement. See below for the explicit definitions of each:

∅c=U Uc=∅

Involution (or double-complement) Law

The involution law covers situations where there is a double-complement. See below for an example:

(Ac)c=A

de Morgan's Law

The rules can be interpreted as:

The complement of the union of two sets is the same as the intersection of their complements

The complement of the intersection of two sets is the same as the union of their complements.

DeMorgan's First Law: (A∪B)^c=AcB^c

DeMorgan's Second Law: (AB)^c=A^c ∪ B^c

DeMorgan's Laws give one the ability to put an intersection (AND) in terms of a union (OR) and vice-versa when checking the complement of compound conditions.

Example #1: DeMorgan's First Law
Show that (A∪B)^c=A^cB^c, given the following:

S={1,2,3,4,5,6}
A={2,3}
B={3,4,5}
Step 1: Find A∪B and (A∪B)^c
A∪B={2,3}∪{3,4,5}={2,3,4,5}
(A∪B)^c={1,6}

Step 2: Find A^c and Bc
A^c={1,4,5,6}
B^c={1,2,6}

Step 3: Find A^cB^c
A^cB^c={1,6}

Step 4: Compare (A∪B)c and AcBc
(A∪B)^c={1,6}=A^cB^c

Solution
It can be shown that (A∪B)^c=A^cB^c, as stated in DeMorgan's first law.




Example #2: DeMorgan's Second Law
Show that (AB)^c=A^c∪B^c, given the following:

S={1,2,3,4,5,6}
A={2,3}
B={3,4,5}
Step 1: Define AB and (AB)^c
AB={3}
(AB)^c={1,2,4,5,6}

Step 2: Define Ac and Bc
Ac={1,4,5,6}
Bc={1,2,6}

Step 3: Find A^c ∪ B^c
Ac∪Bc={1,2,4,5,6}

Solution
It is shown that (AB)^c=A^c∪B^c, as stated in DeMorgan's second law.

# Define the function
def check_numbers_2(m, n):
    # Return False if neither number is positive
    if not m > 0 and not n > 0:
        return False

    # Return True if both numbers are even
    if m % 2 == 0 and n % 2 ==0:
        return True

    # Return False otherwise
    return False

# Define the function
def check_numbers_2(m, n):
    # Return False if neither number is positive
    if not m > 0 and not n > 0:
        return False

    # Return True if both numbers are even
    if m % 2 == 0 and n % 2 ==0:
        return True

    # Return False otherwise
    return False

Subset

In set theory, a set A is a subset of a set B, denoted A⊆B, if and only if every member of A is also contained in B. That is, all elements of A are also elements of B.

Superset

Equivalently to the set A being a subset of the set B above, B is a superset of A. That is B contains all members of A.

Proper Subset

If the set A is a subset of B, and B contains and at least one sample point which is not also contained in A, then A is a proper subset of B, denoted A⊂B.

Additional Properties of Inclusion

A set A is a subset of B if and only if their intersection is equal to A. That is, A⊆B⇔A∩B=A A set A is a subset of B if and only if their union is equal to B. That is, A⊆B⇔A∪B=B

Equality

The equality of two events can be determined through the examination of inclusion. If an event A is a subset of event B and B is also a subset of event A; it can be determined that the events A and B are equal.

Subsets and Supersets

Both the issubset() and issuperset() methods return a boolean indicating whether the parameterized set is a subset or superset, respectively, of the calling set object. See below for an example:

set2.issubset(set1)