部分空間法による文字認識 - mist-team/mist GitHub Wiki

ここでは，カメラで撮影された数字の認識を例として紹介します． 認識手法には部分空間法を使用します． 部分空間法では，学習段階において主成分分析(PCA)を用いるため，行列演算が必須となります． 本サンプルではMISTを用いた認識手法の実現例を示します．

部分空間法の概要

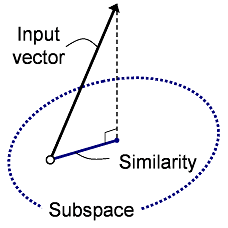
部分空間法は，学習データの集合から，それらの特徴を低次元で表現する部分空間（固有ベクトル）を作成し，それと認識対象の画像との類似度を評価することによって，認識する手法です． サンプル間に存在する変動を吸収する効果があるため，高精度の認識が可能となります．

practice_subspace

準備

画像のサイズ正規化にinterpolate.hを， 行列演算にmatrix.h,numeric.hを使用します．
numeric.hは外部ライブラリを使用しますので，インクルードの際にはLAPACKの準備と 環境設定の項を参照してください．

#include <iostream>
#include <mist.h>
#include <mist/numeric.h>
#include <mist/matrix.h>
#include <mist/io/bmp.h>
#include <mist/interpolate.h>

ここでは，カテゴリを数字の0～9の10種類とし，カテゴリごとに使用する学習データの数は20とします． 画像のサイズは16×16に正規化するものとします． 部分空間の次元，つまり認識に使用する固有ベクトルの数は5と設定します．

const unsigned int category_num = 10;
const unsigned int img_num = 20;
const unsigned int img_size = 16;
const unsigned int eigen_num = 5;

下は実際に使う画像の例(カテゴリ0,1,2)です．

category0 category1 category2

画像の前処理

画像データを扱うためには，前処理としてデータを正規化ベクトルに変換する必要があります． 具体的には，画像をラスタスキャン方式でベクトル化し，そのベクトルを要素の平均が0，ノルムが1となるように変換します． 以下のそのための関数です．

// 画像をラスタスキャンにより正規化ベクトルに変換
void image_to_vector( const mist::array2< unsigned char > &img, mist::matrix< double > &vec )
{
 //ベクトル化
 vec.resize( img.size( ), 1 );
 for( size_t i = 0 ; i < vec.rows( ) ; i ++ )
 {
   vec( i, 0 ) = img[ i ];
 }

 //  平均0
 double mean = 0;
 for( size_t i = 0 ; i < vec.rows( ) ; i ++ )
 {
   mean += vec( i, 0 );
 }
 mean /= static_cast< double >( vec.rows( ) );
 for( size_t i = 0 ; i < vec.rows( ) ; i ++ )
 {
   vec( i, 0 ) -= mean;
 }

 // ノルム1
 double norm = 0;
 for( size_t i = 0 ; i < vec.rows( ) ; i ++ )
 {
   norm += ( vec( i, 0 ) * vec( i, 0 ) );
 }
 norm = std::sqrt( norm );
 for( size_t i = 0 ; i < vec.rows( ) ; i ++ )
 {
   vec( i, 0 ) /= norm;
 }
}

学習段階

n個の学習データx0, x1, ... , xnから部分空間を作成する方法を説明します． ここで，学習データは上で説明したように正規化されたベクトルであるとします． はじめに，これらのベクトルを横に並べた行列Xを作ります． 要素数は(画素数)×(学習データ数)です．

X = [x1, ... , xn]

さらに，この行列の自己相関行列Qを作ります．

Q = X Xt

この行列Qを固有値展開すれば，固有ベクトル[e1, ... , er] (r<n) が得られます．これを認識に利用します． 下に示すサンプルでは，数字0~9までの固有ベクトルを求めています．

// 学習
void training( mist::array1< mist::matrix< double > > &eigen )
{
 char filename[ 256 ];

 mist::array2< unsigned char > img;
 mist::array2< unsigned char > img_n;
 mist::matrix< double > vec;
 mist::matrix< double > mat;
 mist::matrix< double > eval, evec;

 for( unsigned int c = 0 ; c < category_num ; c ++ )
 {
   mat.resize( img_size * img_size, img_num );
   for( size_t i = 0 ; i < img_num ; i ++ )
   {
     // 画像読み込み
     sprintf( filename, "trainingdata/C%d_%02d.bmp", c, i );
     mist::read_bmp( img, filename );

     // サイズ正規化
     mist::linear::interpolate( img, img_n, img_size, img_size );

     // 正規化ベクトルに変換
     image_to_vector( img_n, vec );

     for( size_t j = 0 ; j < vec.rows( ) ; j ++ )
     {
       mat( j, i ) = vec( j, 0 );
     }
   }

   // 自己相関行列
   printf( "Constructing eigenvectors of %d\n", c );
   mat = mat * mat.t( );

   // 固有値・固有ベクトル計算
   mist::eigen( mat, eval, evec );
   eigen( c ) = evec;
   visualize_eigenvectors( evec, c );
 }
}

望み通り固有ベクトルが作成できているかどうか，固有ベクトルを画像化することで確かめられます． その関数を下に示します．

// ベクトルの画像化
void visualize_eigenvectors( const mist::matrix< double > &vec, const unsigned int c )
{
 char filename[ 256 ];
 mist::array2< unsigned char > img( img_size, img_size );
 for( size_t r = 0 ; r < eigen_num ; r ++ )
 {
   double max = -10000;
   double min = 10000;
   for( size_t i = 0 ; i < vec.rows( ) ; i ++ )
   {
     max = ( vec( i, r ) > max ) ? vec( i, r ) : max;
     min = ( vec( i, r ) < min ) ? vec( i, r ) : min;
   }
   for( size_t i = 0 ; i < img.size( ) ; i ++ )
   {
     img[ i ] = static_cast< unsigned char >( 255 * ( vec( i, r ) - min ) / ( max - min ) );
   }
   sprintf( filename, "eigen_img/C%d_%02d.bmp", c, r );
   mist::write_bmp( img, filename );
 }
}

これによって下のような固有ベクトル(カテゴリ0)が作成できていることが確認できれば，学習は成功です．

eigen2_1 eigen2_2 eigen2_3

なお，このような画像の代わりに，全体にノイズがかかったような画像しか得られなかった場合，固有ベクトルが反対の順序で整列されてしまった可能性があります． numeric.hを使って部分空間を作成する際には，気をつけなければいけないことがあります． mistのデフォルトの設定では，固有ベクトルを固有値の小さい順に整列するようになっています． 大きい順に整列させるためには，config/mist_conf.hを編集し，

#define _DESCENDING_ORDER_EIGEN_VALUE_      1

と変更します． この設定は忘れやすいので注意しましょう．

認識段階

部分空間法では，各カテゴリに対する類似度を，入力ベクトルとカテゴリの固有ベクトルとの内積の2乗和と定義します． 入力ベクトルをyとすると，この類似度は

∑r (y t er)2

と表すことができます． この類似度を最大とするカテゴリを認識結果とします． 類似度を求める関数と，認識の処理は以下のようになります．

// 類似度の計算
double similarity( const mist::matrix< double > &ivec, const mist::matrix< double > &evec )
{
 mist::matrix< double > inner_product = ivec.t( ) * evec;
 double sim = 0.0;
 for( size_t i = 0 ; i < eigen_num ; i ++ )
 {
   // 内積の2乗和
   sim += ( inner_product( 0, i ) * inner_product( 0, i ) );
 }
 return sim;
}

// 認識
void recognition( const mist::array2< unsigned char > &input,  const mist::array1< mist::matrix< double > > &eigen )
{

 mist::array2< unsigned char > img;
 mist::matrix< double > ivec;

 // サイズ正規化
 mist::linear::interpolate( input, img, img_size, img_size, 1 );

 // 正規化ベクトルに変換
 image_to_vector( img, ivec );

 double max_sim = -1;
 double sim;
 unsigned int max_character;

 for( size_t c = 0 ; c < category_num ; c ++ )
 {
   // 類似度が最大となるカテゴリに分類
   sim = similarity( ivec, eigen( c ) );
   if( sim > max_sim )
   {
     max_sim = sim;
     max_character = c;
   }
 }
 printf( "Recognition result is %d\n", max_character );
}

以上の処理によって文字を学習し認識する処理の流れは次のように記述できます．

int main( void )
{
 mist::array1< mist::matrix< double > > eigen( category_num );

 // 学習
 training( eigen );

 char filename[ 256 ];
 mist::array2< unsigned char > input;

 // 各カテゴリのテストデータに対し認識率を求める
 for( unsigned int c = 0 ; c < category_num ; c ++ )
 {
   printf( "Testdata is %d\n", c );
   sprintf( filename, "testdata/C%d.bmp", c );
   mist::read_bmp( input, filename );
   recognition( input, eigen );
 }
 return 0;
}
⚠️ **GitHub.com Fallback** ⚠️