Infinite ground plane using GLSL shaders - martin-pr/possumwood GitHub Wiki
A simple ground plane is used by almost all modeling programs. The simplest approach uses a single polygon passed through to represent a ground plane, with a texture applied to add a sense of scale.
In this tutorial, we will explore an alternative method using a single vieport quad. Compared to the trivial implementation, this approach does not require the scale of the scene (and of the ground polygon) to be determined beforehand, effectively synthesizing an "infinite" ground plane.
Following the initial steps of the Skybox tutorial, we will start with a basic shader setup, utilizing the render/vertex_data/background node. Instantiating all relevant nodes, and connecting them accordingly, leads to the following setup:
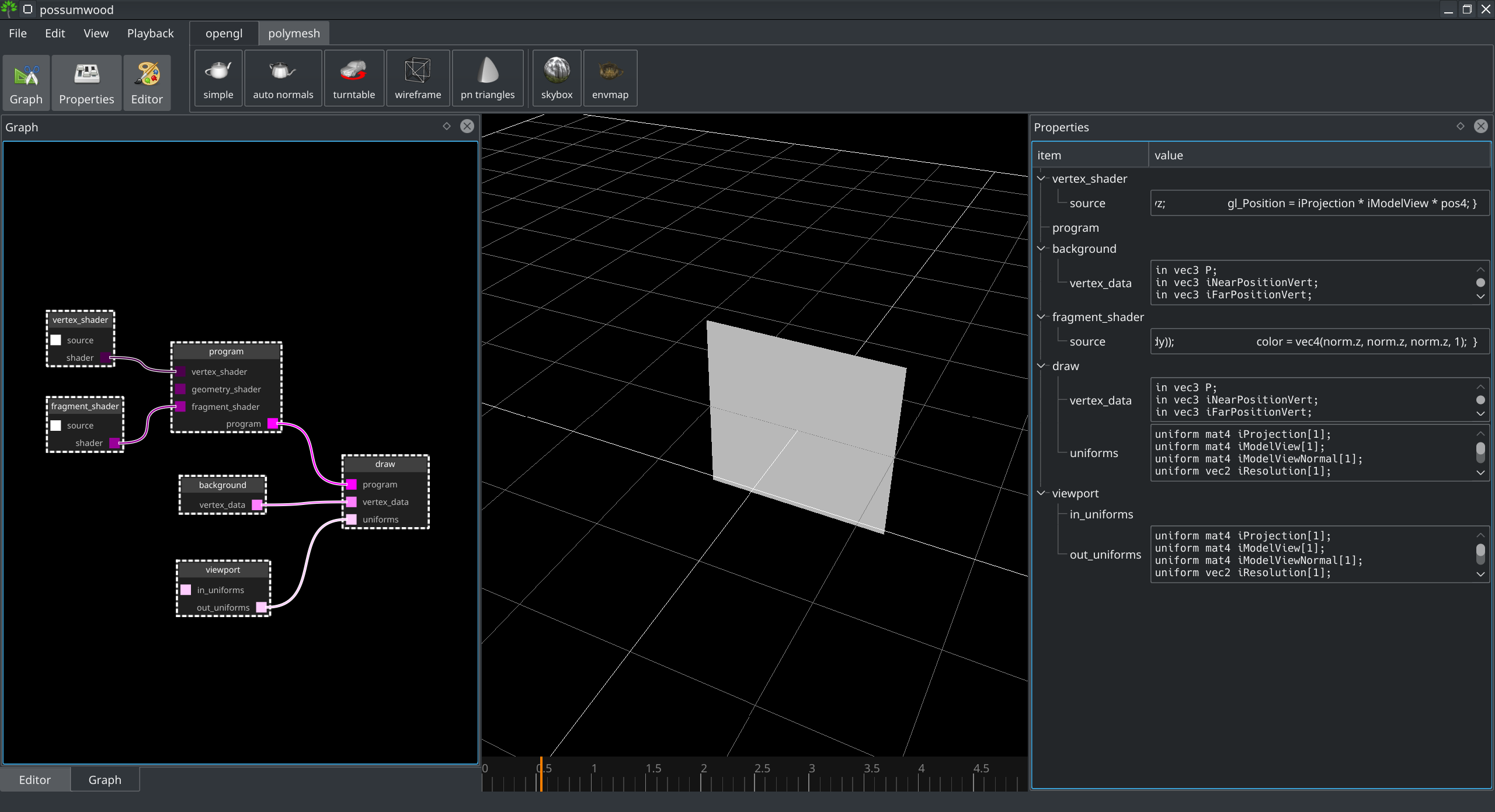
Currently, the plane is in the world space, and it is white. Let's add a simple checker pattern to allow us to see what is going on in our scene. First, let's replace the vertex shader with a shader that passes through the P attribute unchanged:
#version 130
in vec3 P; // position attr from the vbo
uniform mat4 iProjection; // projection matrix
uniform mat4 iModelView; // modelview matrix
out vec3 vertexPosition; // vertex position for the fragment shader
void main() {
vertexPosition = P.xyz;
gl_Position = iProjection * iModelView * vec4(P, 1);
}We can then use round() function to produce a simple checkerboard patter in the fragment shader:
#version 130
out vec4 color;
in vec3 vertexPosition;
void main() {
float c = (
int(round(vertexPosition.x * 5.0)) +
int(round(vertexPosition.y * 5.0))
) % 2;
color = vec4(vec3(c/2.0 + 0.3), 1);
}Which adds a checkerboard pattern to our plane:

Finally, to make our shader into a "background shader", we need to alter the vertex shader to remove any modelview or projective transformations, effectively moving our plane into clip coordinates:
#version 130
in vec3 P; // position attr from the vbo
out vec3 vertexPosition; // vertex position for the fragment shader
void main() {
vertexPosition = P.xyz;
gl_Position = vec4(P, 1);
}The resulting checkerboard image covers the whole camera view, and does not react to camera movement.

The render/vertex_data/background_shader node provides three per-vertex data - P is the world-space position; the iNearPositionVert and iFarPositionVert provide the same information, but transformed using gluUnProject() function, effectively remapping the near and far planes from camera space to world space (the Skybox tutorial contains more details about this).
By using these in the fragment shader, we obtain per-pixel world space position values on the near and far plane (Pnear and Pfar respectively). We can then describe a per-pixel camera ray using a parametric equation of a line with parameter t:
The ray intersects the ground when Y component of ray R equals zero:
Which leads to:
When t > 0, the ray intersected the ground in front of the camera - the ground should be rendered. When t ≤ 0, the ground intersection would be behind the camera - the ray is aiming towards the sky.
In practice, we need to first modify the vertex shader to pass through the near and far plane positions:
#version 130
in vec3 P;
in vec3 iNearPositionVert;
in vec3 iFarPositionVert;
out vec3 vertexPosition;
out vec3 near;
out vec3 far;
void main() {
vertexPosition = P;
near = iNearPositionVert;
far = iFarPositionVert;
gl_Position = vec4(P, 1);
}Using the near and far values, we can then compute t, and use it to distinguish the intersection with the ground:
#version 130
out vec4 color;
in vec3 vertexPosition;
in vec3 near;
in vec3 far;
void main() {
float c = (
int(round(vertexPosition.x * 5.0)) +
int(round(vertexPosition.y * 5.0))
) % 2;
float t = -near.y / (far.y-near.y);
color = vec4(vec3(c/2.0 + 0.3), 1);
color = color * float(t > 0);
}This leads to our fragment shader showing the grid pattern only when we're intersecting with the ground:

Using parameter t computed in the previous section, we can compute the 3D position of the ground intersection using the original equation of a line:
This allows us to compute Rx and Rz, which can then be used to create checkerboard pattern placed on the ground:
#version 130
out vec4 color;
in vec3 vertexPosition;
in vec3 near;
in vec3 far;
void main() {
float t = -near.y / (far.y-near.y);
vec3 R = near + t * (far-near);
float c = (
int(round(R.x * 5.0)) +
int(round(R.z * 5.0))
) % 2;
color = vec4(vec3(c/2.0 + 0.3), 1) * float(t > 0);
}This leads to checkerboard pattern on the ground, stretching all the way to infinity:

We can improve on the pattern by adding multiple resolutions:
#version 130
out vec4 color;
in vec3 vertexPosition;
in vec3 near;
in vec3 far;
float checkerboard(vec2 R, float scale) {
return float((
int(floor(R.x / scale)) +
int(floor(R.y / scale))
) % 2);
}
void main() {
float t = -near.y / (far.y-near.y);
vec3 R = near + t * (far-near);
float c =
checkerboard(R.xz, 1) * 0.3 +
checkerboard(R.xz, 10) * 0.2 +
checkerboard(R.xz, 100) * 0.1 +
0.1;
color = vec4(vec3(c/2.0 + 0.3), 1) * float(t > 0);
}Leading to an infinite ground with multiple resolution of grids:

Unfortunately, this simple approach leads to severe aliasing artifacts. A simple way to address these is to fade the pattern to zero, creating a simple "spotlight" effect:
#version 130
out vec4 color;
in vec3 vertexPosition;
in vec3 near;
in vec3 far;
float checkerboard(vec2 R, float scale) {
return float((
int(floor(R.x / scale)) +
int(floor(R.y / scale))
) % 2);
}
void main() {
float t = -near.y / (far.y-near.y);
vec3 R = near + t * (far-near);
float c =
checkerboard(R.xz, 1) * 0.3 +
checkerboard(R.xz, 10) * 0.2 +
checkerboard(R.xz, 100) * 0.1 +
0.1;
c = c * float(t > 0);
float spotlight = min(1.0, 1.5 - 0.02*length(R.xz));
color = vec4(vec3(c*spotlight), 1);
}Leading to a procedural infinite ground plane result with the "spotlight" effect:

To test how this setup behaves with multiple object in the scene, let's create a teapot via opengl/simple toolbar item:

It looks like the teapot is fully visible, even though at least half of it should be hidden by the ground!
To fix this, we need out fragment shader to output a correct per-fragment depth value using gl_FragDepth function, instead of relying on the fixed-functionality "early" depth test. The depth value needs to be represented in clip coordinates, and converted to the range contained in the gl_DepthRange uniform:
// computes Z-buffer depth value, and converts the range.
float computeDepth(vec3 pos) {
// get the clip-space coordinates
vec4 clip_space_pos = iProjection * iModelView * vec4(pos.xyz, 1.0);
// get the depth value in normalized device coordinates
float clip_space_depth = clip_space_pos.z / clip_space_pos.w;
// and compute the range based on gl_DepthRange settings (not necessary with default settings, but left for completeness)
float far = gl_DepthRange.far;
float near = gl_DepthRange.near;
float depth = (((far-near) * clip_space_depth) + near + far) / 2.0;
// and return the result
return depth;
}For further explanation, please have a look at this stack overflow post.
Plugging this to the fragment shader source:
#version 130
out vec4 color;
in vec3 vertexPosition;
in vec3 near;
in vec3 far;
uniform mat4 iProjection;
uniform mat4 iModelView;
float checkerboard(vec2 R, float scale) {
return float((
int(floor(R.x / scale)) +
int(floor(R.y / scale))
) % 2);
}
float computeDepth(vec3 pos) {
vec4 clip_space_pos = iProjection * iModelView * vec4(pos.xyz, 1.0);
float clip_space_depth = clip_space_pos.z / clip_space_pos.w;
float far = gl_DepthRange.far;
float near = gl_DepthRange.near;
float depth = (((far-near) * clip_space_depth) + near + far) / 2.0;
return depth;
}
void main() {
float t = -near.y / (far.y-near.y);
vec3 R = near + t * (far-near);
float c =
checkerboard(R.xz, 1) * 0.3 +
checkerboard(R.xz, 10) * 0.2 +
checkerboard(R.xz, 100) * 0.1 +
0.1;
c = c * float(t > 0);
float spotlight = min(1.0, 1.5 - 0.02*length(R.xz));
color = vec4(vec3(c*spotlight), 1);
gl_FragDepth = computeDepth(R);
}This leads to a setup with correct depth handling, with our teapot half-submerged in the ground plane:
