Geometry Shader Tessellation using PN Triangles - martin-pr/possumwood GitHub Wiki
Tessellation in computer graphics is a technique allowing to add smooth detail to a coarse input mesh. In principle, the coarse set of input polygons (patches) is interpolated using a non-linear interpolation technique (such as a Bezier surface or Catmull–Clark subdivision surface ), creating additional (smaller) polygons.
A number of subdivision surface techniques exist, many with direct applications and implementations in computer graphics. Modern OpenGL pipeline even includes specific Tessellation shaders, addressing surface refining in hardware.
In this tutorial, we will have a look at one specific technique, Curved PN Triangles, introduced by Alex Vlachos, et al. on I3D 2001 [1].

This technique differs from other techniques mentioned above in several details:
- it only uses information of a single polygon (triangle) at a time
- it makes use of data commonly available in 3D graphics pipeline - per-vertex positions and normals
- it can be easily implemented in a geometry shader, with a simple
triangleslayout input - it uses simple polynomial patches to represent the surface and normals (a cubic patch for vertices and a quadratic patch for normals)
However, the techniques introduced here are not suitable to use in practice - geometry shader processing is known to be slow and unsuitable for subdivision tasks, with the bespoke OpenGL 4 tessellation pipeline providing significantly better performance in practice.
As a starting point, let's bring in the simple setup from the toolbar, which will create a simple teapot rendering in our viewport.
As a test case, we will be working with two models simultaneously - one will be the teapot we already have in our scene, and the other one will be a simple tetrahendron. Both should be sharing the same shader source, but different source of vertex data. This leads to the following setup:

The main problem with this setup is the huge difference of scale - the tetrahendron is completely enveloped by the teapot! By adding two additional render/uniforms/transform nodes and adjusting the vertex program, we can easily fix that:

First, we need to change the vertex shader to take our new uniform into account:
#version 130
out vec3 vertexNormal;
out vec3 vertexPosition;
in vec3 P;
in vec3 N;
uniform mat4 iProjection;
uniform mat4 iModelView;
uniform mat4 iModelViewNormal;
uniform mat4 tr;
void main() {
vec4 pos4 = vec4(P.x, P.y, P.z, 1);
vertexNormal = (iModelViewNormal * tr * vec4(N.x, N.y, N.z, 0)).xyz;
vertexPosition = (iModelView * tr * vec4(P.x, P.y, P.z, 1)).xyz;
gl_Position = iProjection * iModelView * tr * vec4(P.x, P.y, P.z, 1);
}
We have named our uniform tr, so let's adjust the attributes on the transform nodes accordingly, and scale the teapot to 0.02, while moving it two units of the world space on the X axis:

Repeating the same steps for the second transform node, we can easily achieve the effect above.
Similarly as in the previous Wireframe tutorial, we need a geometry shader in our setup. Simply instancing and plugging it doesn't lead to a functional setup, however:

We need to adjust the geometry shader to pass the per-vertex values through. However, we can also move part of the functionality to the geometry shader, to allow it to work on world-space data.
The vertex shader will then only apply the world-space transformations, avoiding even the call to gl_Position (no longer necessary with a geometry shader):
#version 130
out vec3 normal;
out vec3 position;
in vec3 P;
in vec3 N;
uniform mat4 iModelView;
uniform mat4 iModelViewNormal;
uniform mat4 tr;
void main() {
normal = (iModelViewNormal * tr * vec4(N.x, N.y, N.z, 0)).xyz;
position = (iModelView * tr * vec4(P.x, P.y, P.z, 1)).xyz;
}
The geometry shader then applies the necessary projection transformation, and passes the vertex data to the fragment shader:
#version 150
layout(triangles) in;
layout(triangle_strip, max_vertices = 3) out;
uniform mat4 iProjection;
in vec3 normal[];
in vec3 position[];
out vec3 vertexNormal;
out vec3 vertexPosition;
void main() {
for(int i = 0; i < 3; i++) {
vertexNormal = normal[i];
vertexPosition = position[i];
gl_Position = iProjection * vec4(position[i], 1);
EmitVertex();
}
EndPrimitive();
}
With these changes, we are back to where we started, at least visually:

As the next step, lets colour each polygon differently, to highlight the polygon density. For this, we will use an in-built geometry shader variable gl_PrimitiveIDIn, and modulo:
#version 150
layout(triangles) in;
layout(triangle_strip, max_vertices = 3) out;
uniform mat4 iProjection;
in vec3 normal[];
in vec3 position[];
out vec3 vertexNormal;
out vec3 vertexPosition;
out vec3 polygonColour;
vec3 colour(int id) {
return vec3(
float(id % 4) / 3.0,
float((id/4) % 4) / 3.0,
float((id/16) % 4) / 3.0
);
}
void main() {
for(int i = 0; i < 3; i++) {
vertexNormal = normal[i];
vertexPosition = position[i];
polygonColour = colour(gl_PrimitiveIDIn + 1);
gl_Position = iProjection * vec4(position[i], 1);
EmitVertex();
}
EndPrimitive();
}
The fragment shader will then need to apply the colour value:
#version 130
out vec4 color;
in vec3 vertexNormal;
in vec3 polygonColour;
void main() {
vec3 norm = normalize(vertexNormal);
float val = abs(norm.z);
color = vec4(polygonColour * val, 1);
}
Leading to very colourful primitives:
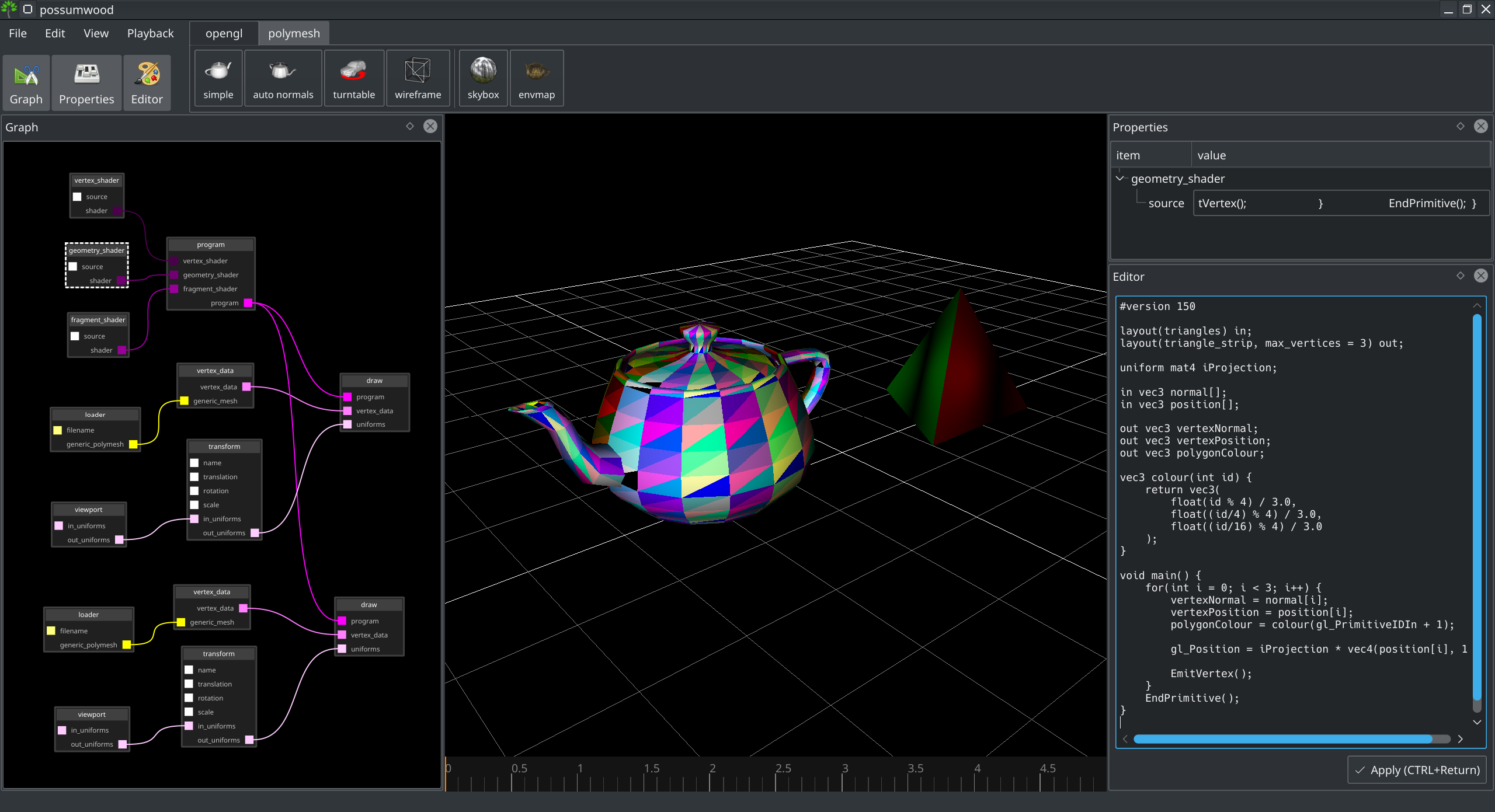
The first step of the subdivision algorithm is to split input triangles into smaller ones, allowing to represent more geometry detail. In our implementation, we will focus only on individual triangles, and we will not try to adaptively subdivide the surface based on surface detail or curvature. Each triangle will be subdivided into smaller triangles uniformly, and all new triangles will lie in the same plane as the original triangle.
To achieve this, we will make use of barycentric coodrinates, which provide a very simple way to parametrize a triangle:
Parameterising on u and v, we can then subdivide the original triangle into smaller triangles, each subdivision level adding 2 more triangles than the previous level (i.e., 1, 1+3, 1+3+5, 1+3+5+7...).
The subdivided triangle can be rendered using a set of triangle strips, one for each subdivision level, saving on the output vertex count of our geometry shader. The number of vertices for each subdivision level (i.e., each triangle strip) is then determined using an arithmetic progression:
Where n is the subdivision level.
The total number of output vertices of the compute shader is computed via its sum:
This leads to the following vertex counts:
| Subdivision lvl | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vertex count | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 | 120 | 143 | 168 | 195 | 224 | 255 |
Given the usual vertex output limitation of 256 vertices, the maximum subdivision level is 15.
#version 150
// 1 = no subdivision (pass-thru)
// 2 = 4x subdiv
// 3 = 9x subdiv
// 4 = 16x subdiv
// ...
//#define SUBDIV_LEVEL 1
//#define MAX_VERTS 3 // 3
//#define SUBDIV_LEVEL 2
//#define MAX_VERTS 8 // 3+5
#define SUBDIV_LEVEL 15
#define MAX_VERTS 255 // arithmetic progression 15*(6+(15-1)*2)/2
layout(triangles) in;
layout(triangle_strip, max_vertices = MAX_VERTS) out;
uniform mat4 iProjection;
in vec3 normal[];
in vec3 position[];
out vec3 vertexNormal;
out vec3 vertexPosition;
out vec3 polygonColour;
vec3 colour(int id) {
return vec3(
float(id % 4) / 3.0,
float((id/4) % 4) / 3.0,
float((id/16) % 4) / 3.0
);
}
vec3 weights(int s, int t) {
vec3 result;
result.x = float(s) / float(SUBDIV_LEVEL);
result.y = float(t) / float(SUBDIV_LEVEL);
result.z = 1.0 - result.x - result.y;
return result;
}
void emitVertex(int s, int t) {
vec3 w = weights(s, t);
vertexNormal = normalize(normal[0]*w[0] + normal[1]*w[1] + normal[2]*w[2]);
vertexPosition = position[0]*w[0] + position[1]*w[1] + position[2]*w[2];
gl_Position = iProjection * vec4(vertexPosition, 1);
EmitVertex();
}
void main() {
for(int level = 0; level < SUBDIV_LEVEL; ++level) {
polygonColour = colour(gl_PrimitiveIDIn*SUBDIV_LEVEL + level);
for(int s = 0; s <= level; ++s) {
emitVertex(s, level-s+1);
emitVertex(s, level-s);
}
emitVertex(level+1, 0);
EndPrimitive();
}
}
This shader renders each triangle strip using a separate colour. With maximum subdivision level, this leads to a "stripy" render:
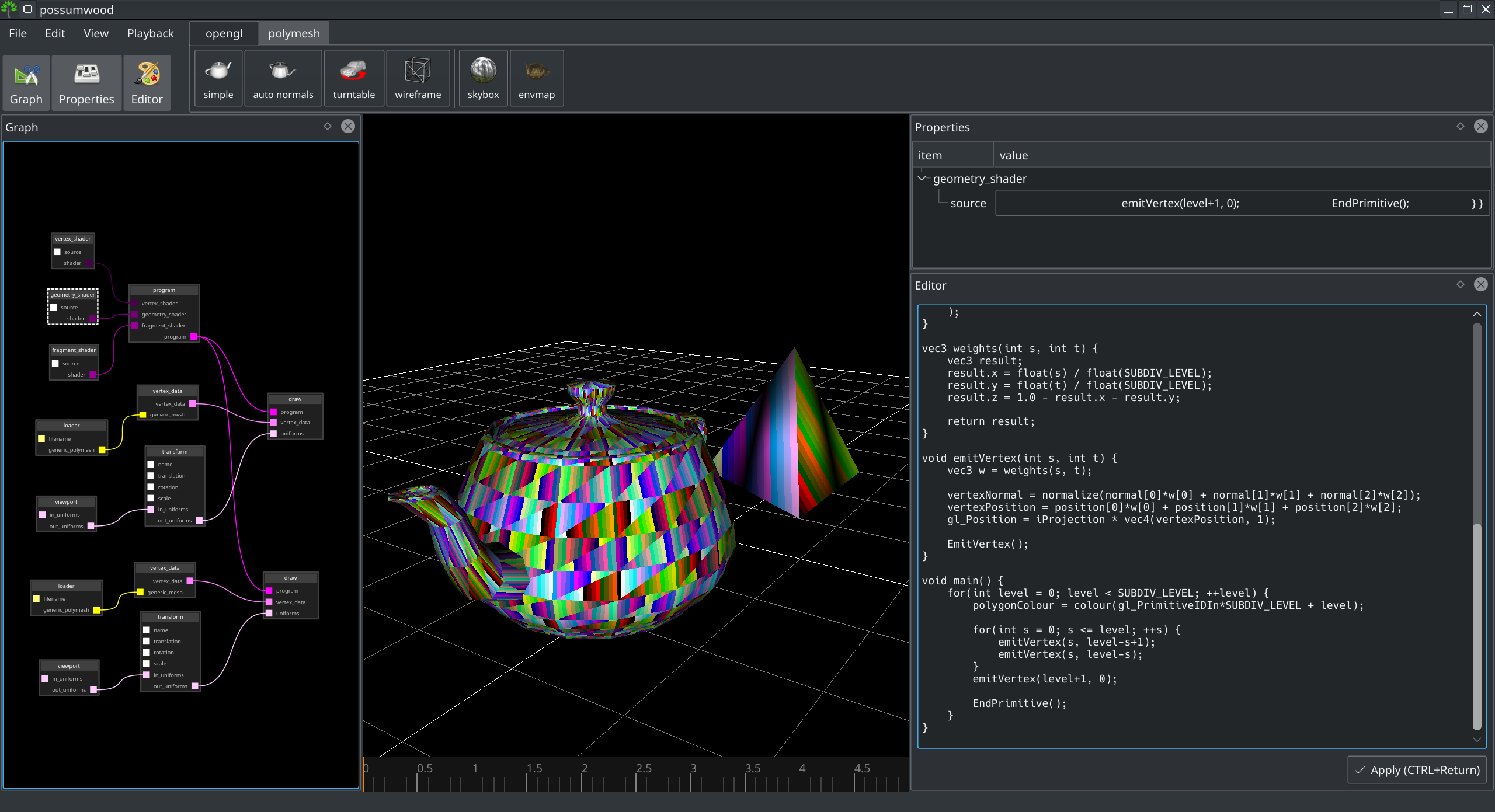
The equations describing the cubic patch is described in Section 3.1 of the original paper [1]. In this section, we will not repeat its mathematical description, and focus only on implementation in GLSL.
First, lets update the fragment shader to display per-polygon normals, which simplify the debugging of the geometry shader:
#version 130
out vec4 color;
in vec3 vertexPosition;
in vec3 vertexNormal;
void main() {
//vec3 norm = normalize(vertexNormal);
vec3 norm = normalize(cross(dFdx(vertexPosition), dFdy(vertexPosition)));
float val = abs(norm.z);
color = vec4(val, val, val, 1);
}
We will store the cubic patch data in a structure (Coeffs), which is computed in the body of the shader's main() function. We then use this structure to emit individual vertices of each patch in the emitVertex() function. Finally, a loop in main() will generate separate triangles strips, based on the subdivision level.
#version 150
// 1 = no subdivision (pass-thru)
// 2 = 4x subdiv
// 3 = 9x subdiv
// 4 = 16x subdiv
// ...
//#define SUBDIV_LEVEL 1
//#define MAX_VERTS 3 // 3
//#define SUBDIV_LEVEL 2
//#define MAX_VERTS 8 // 3+5
#define SUBDIV_LEVEL 15
#define MAX_VERTS 255 // arithmetic progression 15*(6+(15-1)*2)/2
layout(triangles) in;
layout(triangle_strip, max_vertices = MAX_VERTS) out;
uniform mat4 iProjection;
in vec3 normal[];
in vec3 position[];
out vec3 vertexNormal;
out vec3 vertexPosition;
struct Coeffs {
vec3 b300, b030, b003,
b210, b120, b021, b012, b102, b201,
b111;
};
vec3 weights(int s, int t) {
vec3 result;
result.x = float(s) / float(SUBDIV_LEVEL);
result.y = float(t) / float(SUBDIV_LEVEL);
result.z = 1.0 - result.x - result.y;
return result;
}
void emitVertex(int s, int t, Coeffs c) {
vec3 w = weights(s, t);
vertexPosition =
c.b300 * pow(w[2], 3) + c.b030 * pow(w[0], 3) + c.b003*pow(w[1], 3) +
c.b210*3*w[2]*w[2]*w[0] + c.b120*3*w[2]*w[0]*w[0] + c.b201*3*w[2]*w[2]*w[1] +
c.b021*3*w[0]*w[0]*w[1] + c.b102*3*w[2]*w[1]*w[1] + c.b012*3*w[0]*w[1]*w[1] +
c.b111*6*w[0]*w[1]*w[2];
w = weights(s, t);
vertexNormal = normalize(normal[0]*w[2] + normal[1]*w[0] + normal[2]*w[1]);
gl_Position = iProjection * vec4(vertexPosition, 1);
EmitVertex();
}
void main() {
Coeffs c;
c.b300 = position[0];
c.b030 = position[1];
c.b003 = position[2];
vec3 n[3];
n[0] = normalize(normal[0]);
n[1] = normalize(normal[1]);
n[2] = normalize(normal[2]);
float w12 = dot(position[1] - position[0], n[0]);
float w21 = dot(position[0] - position[1], n[1]);
float w23 = dot(position[2] - position[1], n[1]);
float w32 = dot(position[1] - position[2], n[2]);
float w31 = dot(position[0] - position[2], n[2]);
float w13 = dot(position[2] - position[0], n[0]);
c.b210 = (2*position[0] + position[1] - w12*n[0]) / 3.0;
c.b120 = (2*position[1] + position[0] - w21*n[1]) / 3.0;
c.b021 = (2*position[1] + position[2] - w23*n[1]) / 3.0;
c.b012 = (2*position[2] + position[1] - w32*n[2]) / 3.0;
c.b102 = (2*position[2] + position[0] - w31*n[2]) / 3.0;
c.b201 = (2*position[0] + position[2] - w13*n[0]) / 3.0;
vec3 E = (c.b210 + c.b120 + c.b021 + c.b012 + c.b102 + c.b201) / 6.0;
vec3 V = (position[0] + position[1] + position[2]) / 3.0;
c.b111 = E + (E - V) / 2.0;
for(int level = 0; level < SUBDIV_LEVEL; ++level) {
for(int s = 0; s <= level; ++s) {
emitVertex(s, level-s+1, c);
emitVertex(s, level-s, c);
}
emitVertex(level+1, 0, c);
EndPrimitive();
}
}
This leads to the following output (notice the additional patches and the "bulging" of the tetrahedron's faces produced by the subdivision):

The final step is to implement the normals generation using a quadratic patch, as described in Section 3.3 of the original paper [1].
To visualise the normals, we need to update the fragment shader to respect the incoming normal value:
#version 130
out vec4 color;
in vec3 vertexPosition;
in vec3 vertexNormal;
void main() {
vec3 norm = normalize(vertexNormal);
float val = abs(norm.z);
color = vec4(val, val, val, 1);
}
The geometry shader then needs to output the correct normal to the vertexNormal output:
#version 150
// 1 = no subdivision (pass-thru)
// 2 = 4x subdiv
// 3 = 9x subdiv
// 4 = 16x subdiv
// ...
//#define SUBDIV_LEVEL 1
//#define MAX_VERTS 3 // 3
//#define SUBDIV_LEVEL 2
//#define MAX_VERTS 8 // 3+5
#define SUBDIV_LEVEL 15
#define MAX_VERTS 255 // arithmetic progression 15*(6+(15-1)*2)/2
layout(triangles) in;
layout(triangle_strip, max_vertices = MAX_VERTS) out;
uniform mat4 iProjection;
in vec3 normal[];
in vec3 position[];
out vec3 vertexNormal;
out vec3 vertexPosition;
struct PCoeffs {
vec3 b300, b030, b003,
b210, b120, b021, b012, b102, b201,
b111;
};
struct NCoeffs {
vec3 n200, n020, n002, n110, n011, n101;
};
vec3 weights(int s, int t) {
vec3 result;
result.x = float(s) / float(SUBDIV_LEVEL);
result.y = float(t) / float(SUBDIV_LEVEL);
result.z = 1.0 - result.x - result.y;
return result;
}
void emitVertex(int s, int t, PCoeffs c, NCoeffs nc) {
vec3 w = weights(s, t);
vertexPosition =
c.b300 * pow(w[2], 3) + c.b030 * pow(w[0], 3) + c.b003*pow(w[1], 3) +
c.b210*3*w[2]*w[2]*w[0] + c.b120*3*w[2]*w[0]*w[0] + c.b201*3*w[2]*w[2]*w[1] +
c.b021*3*w[0]*w[0]*w[1] + c.b102*3*w[2]*w[1]*w[1] + c.b012*3*w[0]*w[1]*w[1] +
c.b111*6*w[0]*w[1]*w[2];
w = weights(s, t);
vertexNormal = normalize(
nc.n200*w[2]*w[2] + nc.n020*w[0]*w[0] + nc.n002*w[1]*w[1] +
nc.n110*w[2]*w[0] + nc.n011*w[0]*w[1] + nc.n101*w[2]*w[1]
);
gl_Position = iProjection * vec4(vertexPosition, 1);
EmitVertex();
}
float nv(vec3 p1, vec3 n1, vec3 p2, vec3 n2) {
return 2.0 * dot(p2-p1, n1+n2) / dot(p2-p1, p2-p1);
}
void main() {
PCoeffs c;
c.b300 = position[0];
c.b030 = position[1];
c.b003 = position[2];
vec3 n[3];
n[0] = normalize(normal[0]);
n[1] = normalize(normal[1]);
n[2] = normalize(normal[2]);
float w12 = dot(position[1] - position[0], n[0]);
float w21 = dot(position[0] - position[1], n[1]);
float w23 = dot(position[2] - position[1], n[1]);
float w32 = dot(position[1] - position[2], n[2]);
float w31 = dot(position[0] - position[2], n[2]);
float w13 = dot(position[2] - position[0], n[0]);
c.b210 = (2*position[0] + position[1] - w12*n[0]) / 3.0;
c.b120 = (2*position[1] + position[0] - w21*n[1]) / 3.0;
c.b021 = (2*position[1] + position[2] - w23*n[1]) / 3.0;
c.b012 = (2*position[2] + position[1] - w32*n[2]) / 3.0;
c.b102 = (2*position[2] + position[0] - w31*n[2]) / 3.0;
c.b201 = (2*position[0] + position[2] - w13*n[0]) / 3.0;
vec3 E = (c.b210 + c.b120 + c.b021 + c.b012 + c.b102 + c.b201) / 6.0;
vec3 V = (position[0] + position[1] + position[2]) / 3.0;
c.b111 = E + (E - V) / 2.0;
////
NCoeffs nc;
nc.n200 = n[0];
nc.n020 = n[1];
nc.n002 = n[2];
nc.n110 = normalize(n[0] + n[1] - nv(position[0], n[0], position[1], n[1])*(position[1]-position[0]));
nc.n011 = normalize(n[1] + n[2] - nv(position[1], n[1], position[2], n[2])*(position[2]-position[1]));
nc.n101 = normalize(n[2] + n[0] - nv(position[2], n[2], position[0], n[0])*(position[0]-position[2]));
////
for(int level = 0; level < SUBDIV_LEVEL; ++level) {
for(int s = 0; s <= level; ++s) {
emitVertex(s, level-s+1, c, nc);
emitVertex(s, level-s, c, nc);
}
emitVertex(level+1, 0, c, nc);
EndPrimitive();
}
}
This leads to the final output of this tutorial - two polygonal surfaces subdivided using the PN Triangles method:

[1]: Vlachos, Alex, et al. "Curved PN triangles." Proceedings of the 2001 symposium on Interactive 3D graphics. ACM, 2001.