Environment mapping - martin-pr/possumwood GitHub Wiki

Environment mapping (or reflection mapping) is a simple technique to approximate reflections of a distant background on a 3D object. As a simple approximation, it produces accurate results only if certain conditions are met:

1. the reflected environment is fully represented in a background texture
2. the background is "sufficiently distant" (i.e., far enough that any incoming rays can be approximated only by their direction, ignoring their source point)
3. the object is convex (i.e., has no self-reflections)

In many ways, environment mapping is similar to a skybox or skydome, which has been covered in a previous tutorial, and shares its limitations.

Starting point

This tutorial builds on the results of previous tutorials - the turntable and the skybox.

As a starting point, we will import the setups from previous tutorials using the simple and skybox buttons on the toolbar, leading to a setup like this:

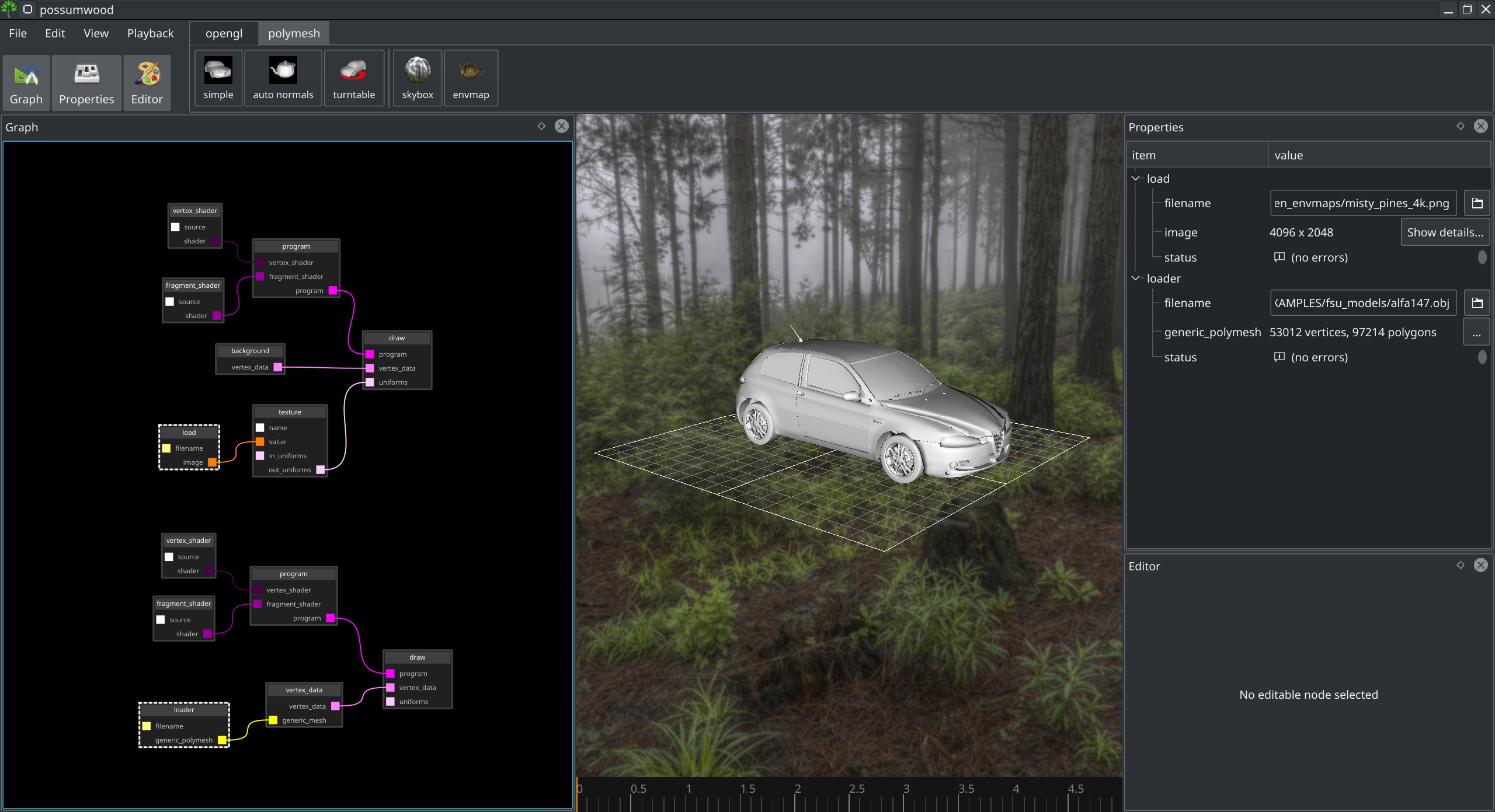
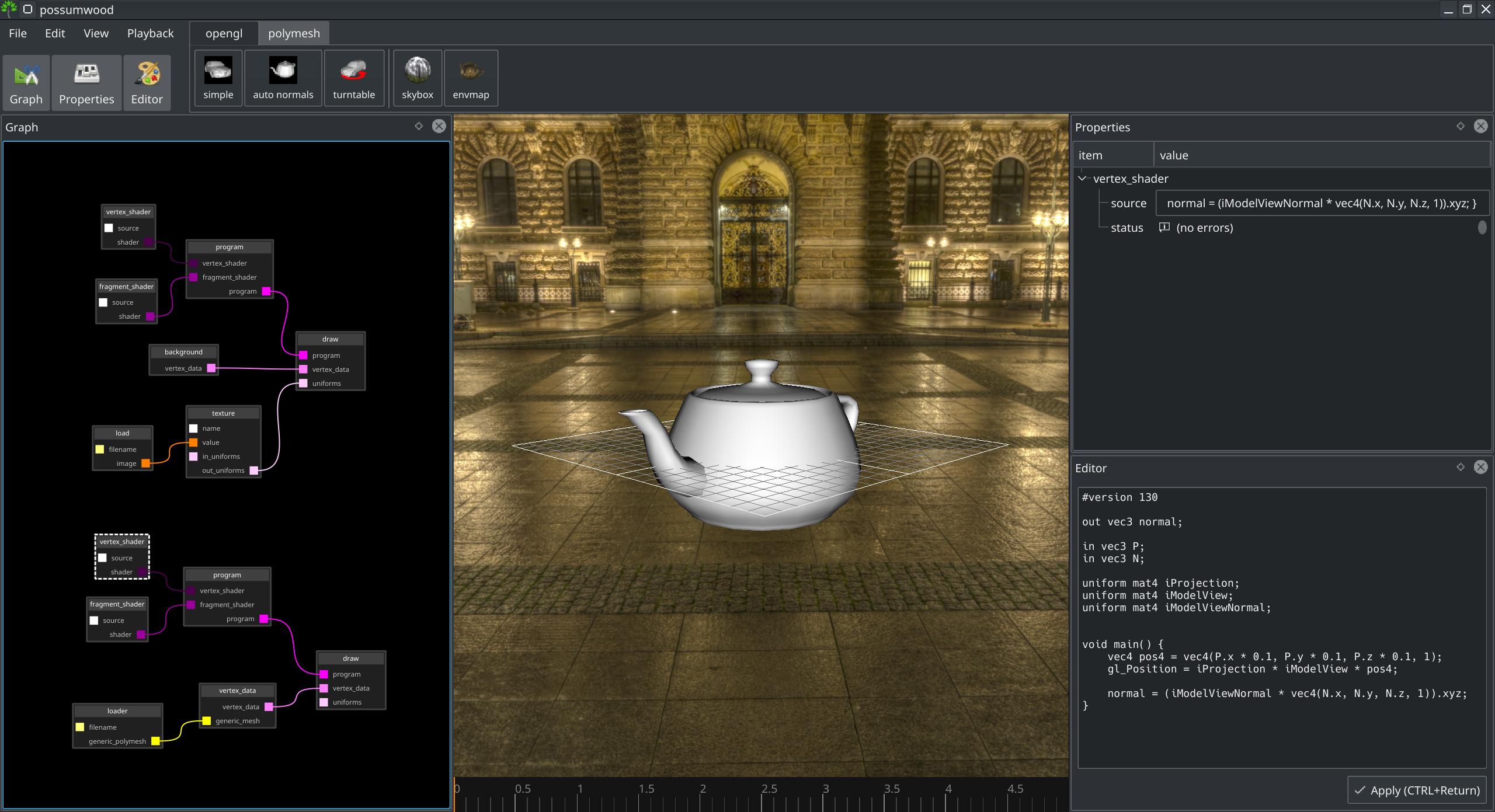
For the specific purposes of this tutorial, let's modify this setup to use the teapot model instead of the car model, change the background to examples/hdrihaven_envmaps/rathaus_8k.png and change the source code of the vertex shader of the model to remove the transformation required for the car model:

#version 130

out vec3 normal;

in vec3 P;
in vec3 N;

uniform mat4 iProjection;
uniform mat4 iModelView;
uniform mat4 iModelViewNormal;


void main() {
	vec4 pos4 = vec4(P.x * 0.1, P.y * 0.1, P.z * 0.1, 1);
	gl_Position = iProjection * iModelView * pos4;

	normal = (iModelViewNormal * vec4(N.x, N.y, N.z, 1)).xyz;
}

These changes lead to a setup that looks like this:

Visualising the normal

As the first step, let's change the shaders to explicitly visualise the world-space normal information.

Vertex shader:

#version 130

in vec3 P;
in vec3 N;

uniform mat4 iProjection;
uniform mat4 iModelView;
uniform mat4 iModelViewNormal;

out vec3 normal;

void main() {
	normal = N;

	vec4 pos4 = vec4(P.x, P.y, P.z, 1);
	gl_Position = iProjection * iModelView * pos4;
}

Fragment shader:

#version 130

out vec4 color;

in vec3 normal;

void main() {
	vec3 norm = normalize(normal);
	color = vec4(normal, 1);
}

This leads to the following:

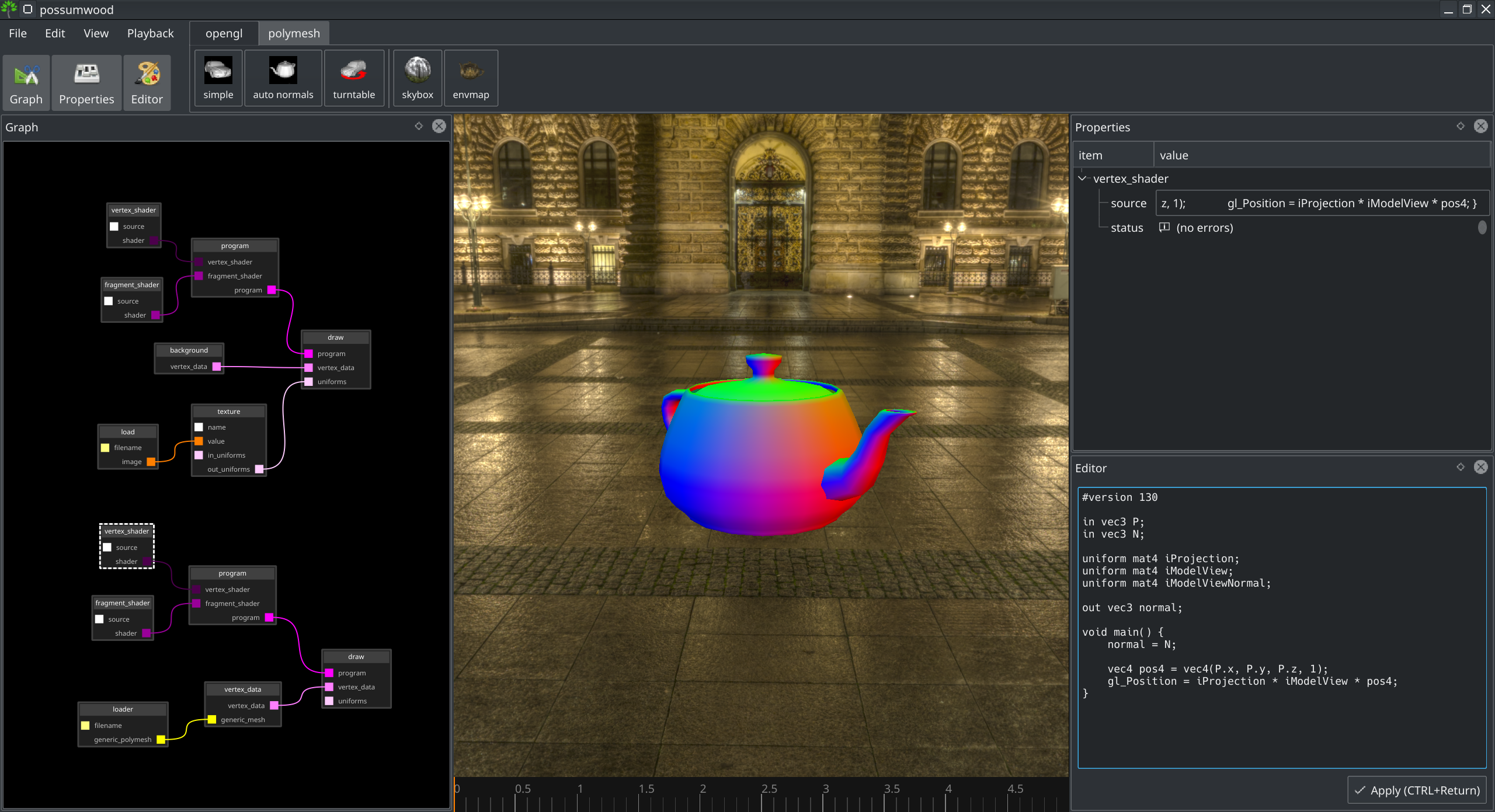
When moving the camera around the scene, you will notice that the teapot always looks like it has been "lit" by a "red light" from the front (direction of the spout), "green light" from the top and "blue light" from the side. This is the consequence of how Possumwood's camera is implemented - the modelview matrix effectively keeps the camera at origin, facing the -Z direction while the objects in the scene are transformed using the modelview matrix. The normal visualisation we have implemented then stays in the world space.

A transparent teapot

As the first step of environment mapping, we need compute a view direction vector from the camera to a point on the teapot's surface for each fragment. This vector will then be altered to provide a sample for reflected colour.

To do that, we will first need to pass the world-space position (a sample on the surface) to the fragment shader:

#version 130

in vec3 P;
in vec3 N;

uniform mat4 iProjection;
uniform mat4 iModelView;
uniform mat4 iModelViewNormal;

out vec3 position;
out vec3 normal;

void main() {
	position = P;
	normal = N;

	vec4 pos4 = vec4(P.x, P.y, P.z, 1);
	gl_Position = iProjection * iModelView * pos4;
}

To derive a view vector for a particular point on a surface, the easiest approach is to determine where the camera's focal point is in the world space, and just subtract it from the surface point in world space.

To determine where our camera is in the world space, we need to multiply a point on the origin (0,0,0,1) with the inverse of the modelview matrix. We could try to derive the inverse in the fragment shader, but that is quite an expensive operation. Instead, we can just use the normal transformation matrix iModelViewNormal, which is the transpose of the inverse of the modelview matrix.

In terms of our shaders, we can derive the normalized direction vector using a simple bit of maths:

// determine the inverse of modelview matrix
mat4 mvInv = transpose(iModelViewNormal);

// get the world-space view vector, by subtracting the world-space camera position
// from world-space surface point
vec3 dir = position - (mvInv * vec4(0,0,0,1)).xyz;
// and normalize the result
dir = normalize(dir);

We can then convert the direction vector to a latlong representation in the same way as in the skybox tutorial:

float lng = acos(dir.y) / 3.1415;
float lat = atan(dir.x, -dir.z) / 3.1415 / 2.0;

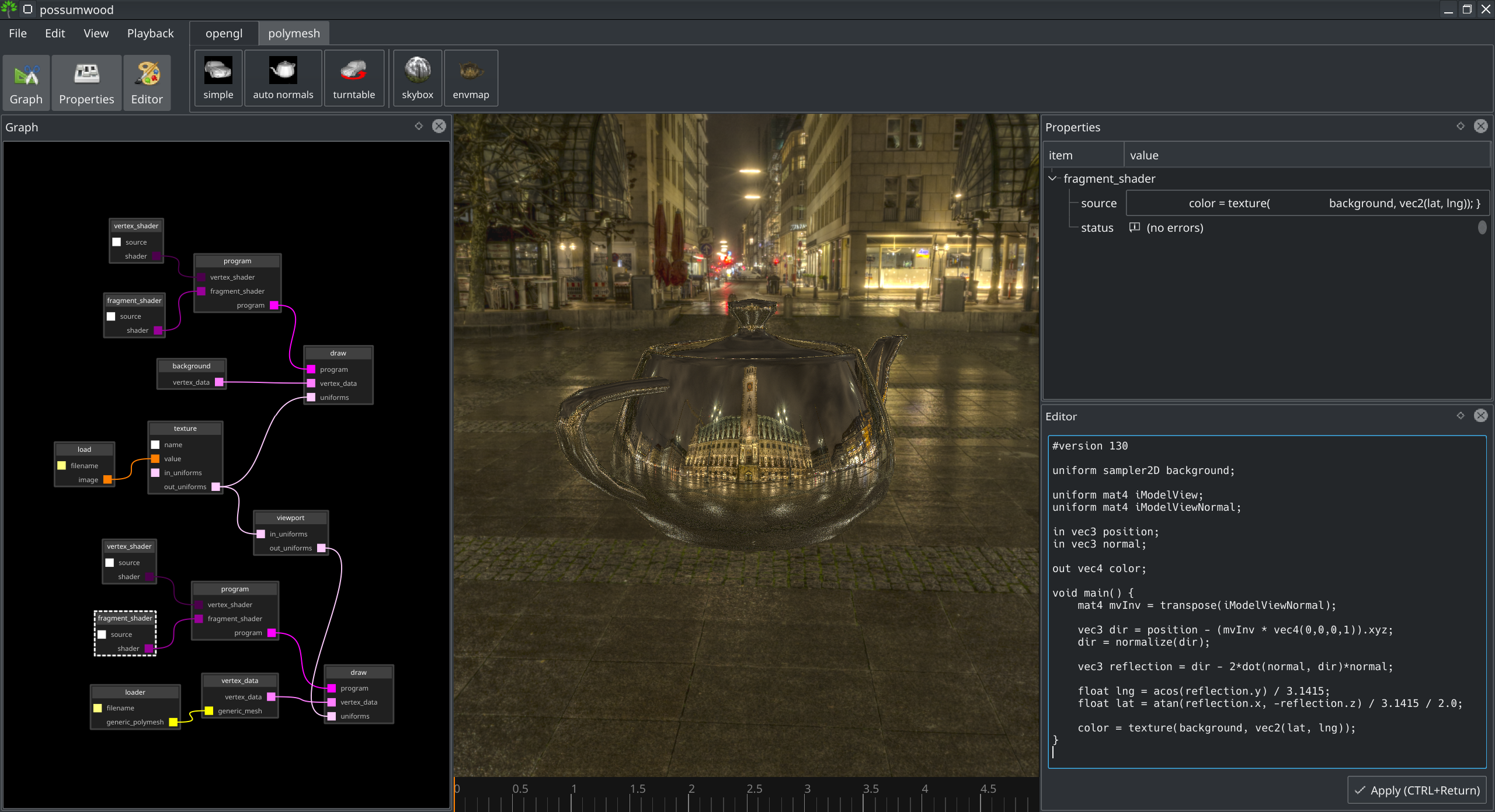
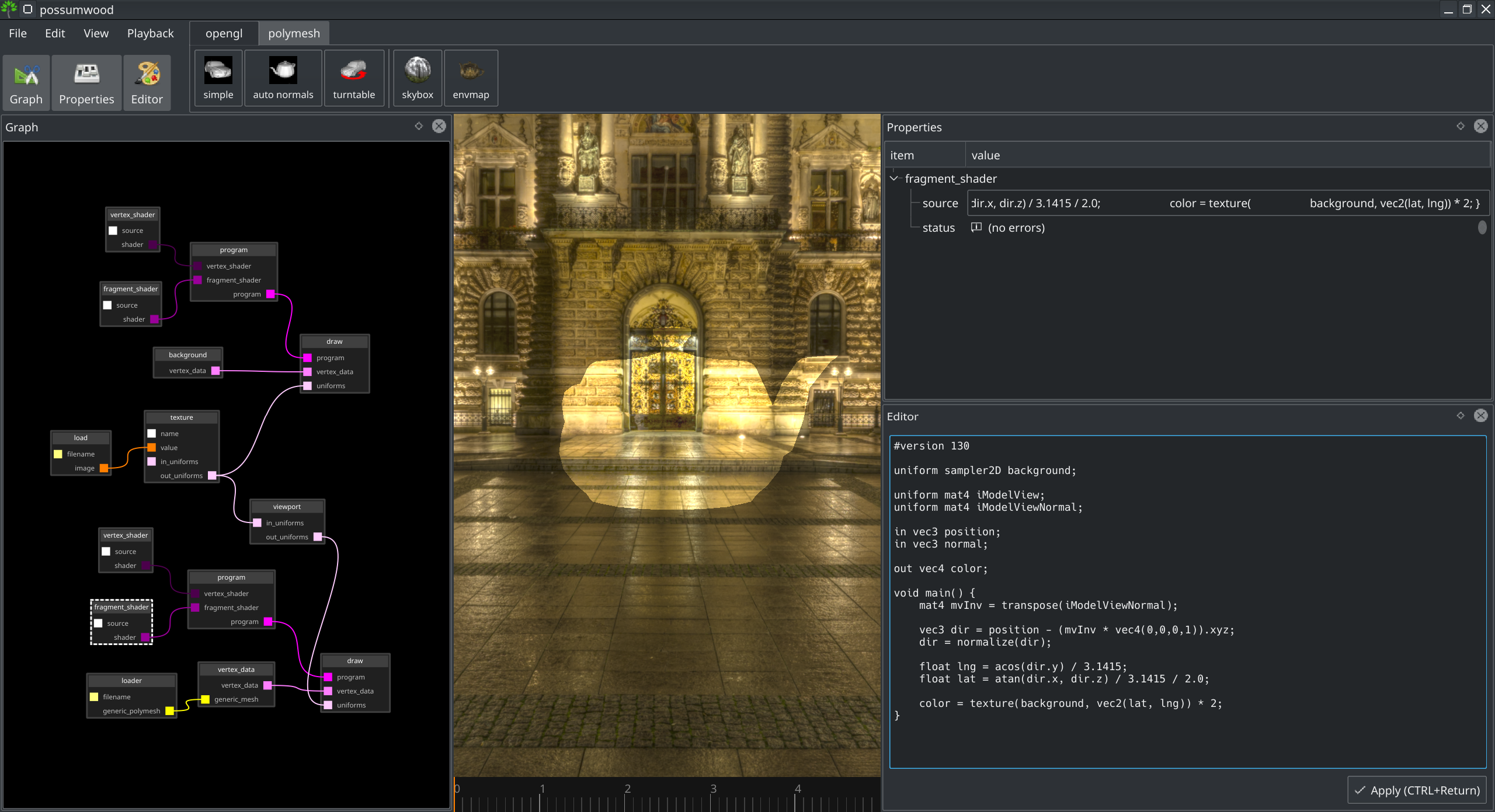
If we use the direction vector without any further manipulation, and use the corresponding lat/long values to query the texture value, the teapot will effectively "disappear" from the viewport, as the returner fragments should be exactly the same as corresponding background colours. To make its outline visible, we can just multiply the returned value by 2.

Putting all together, we arrive at the following fragment shader source:

#version 130

uniform sampler2D background;

uniform mat4 iModelView;
uniform mat4 iModelViewNormal;

in vec3 position;
in vec3 normal;

out vec4 color;

void main() {
	mat4 mvInv = transpose(iModelViewNormal);

	vec3 dir = position - (mvInv * vec4(0,0,0,1)).xyz;
	dir = normalize(dir);

	float lng = acos(dir.y) / 3.1415;
	float lat = atan(dir.x, dir.z) / 3.1415 / 2.0;

	color = texture(background, vec2(lat, lng)) * 2;
}

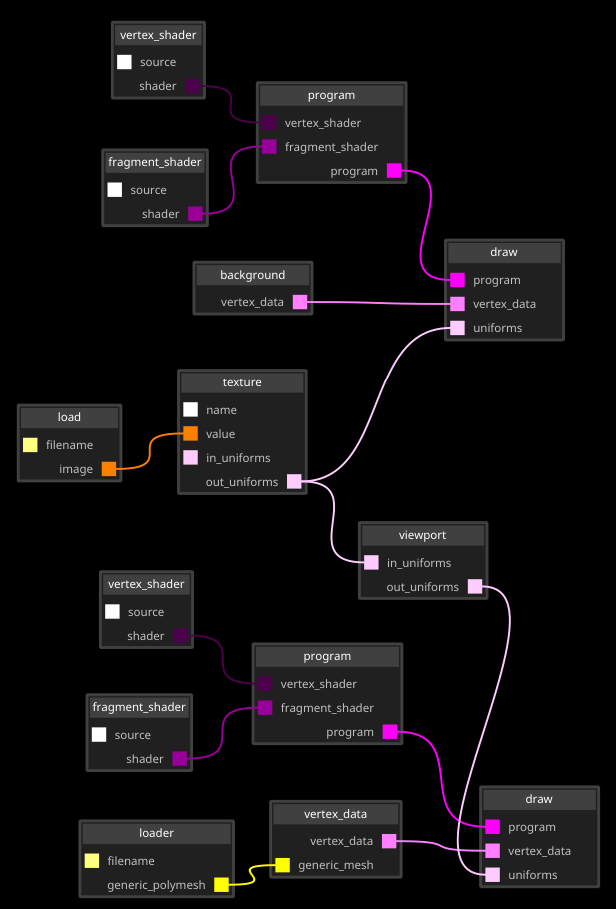
We also need to allow the fragment shader access to the background texture (and the viewport parameters, simultaneously), by changing the structure of the graph, adding the render/uniforms/viewport node and a connection to the background texture:

Leading to a "transparent" teapot effect (which keeps on looking transparent with arbitrary camera movement):

Reflection

Now that we have a world-space view direction vector, and a world-space normal, we can combine them to compute the reflection vector (please see its wikipedia article for a detailed explanation):

vec3 reflection = dir - 2*dot(normal, dir)*normal;

This changes our fragment shader to:

#version 130

uniform sampler2D background;

uniform mat4 iModelView;
uniform mat4 iModelViewNormal;

in vec3 position;
in vec3 normal;

out vec4 color;

void main() {
	mat4 mvInv = transpose(iModelViewNormal);

	vec3 dir = position - (mvInv * vec4(0,0,0,1)).xyz;
	dir = normalize(dir);

	vec3 reflection = dir - 2*dot(normal, dir)*normal;

	float lng = acos(reflection.y) / 3.1415;
	float lat = atan(reflection.x, -reflection.z) / 3.1415 / 2.0;

	color = texture(	background, vec2(lat, lng));
}

And results in a perfectly reflective teapot: