Deadlock, Part 2: Deadlock Conditions - lyuanschool/SystemProgramming GitHub Wiki

Coffman conditions

There are four necessary and sufficient conditions for deadlock. These are known as the Coffman conditions.

• Mutual Exclusion
• Circular Wait
• Hold and Wait
• No pre-emption

All of these conditions are required for deadlock, so let's discuss each one in turn. First the easy ones-

• Mutual Exclusion: The resource cannot be shared
• Circular Wait: There exists a cycle in the Resource Allocation Graph. There exists a set of processes {P1,P2,...} such that P1 is waiting for resources held by P2, which is waiting for P3,..., which is waiting for P1.
• Hold and Wait: A process acquires an incomplete set of resources and holds onto them while waiting for the other resources.
• No pre-emption: Once a process has acquired a resource, the resource cannot be taken away from a process and the process will not voluntarily give up a resource.

Breaking the Coffman Conditions

Two students need a pen and paper:

• The students share a pen and paper. Deadlock is avoided because Mutual Exclusion was not required.
• The students both agree to grab the pen before grabbing the paper. Deadlock is avoided because there cannot be a circular wait.
• The students grab both the pen and paper in one operation ("Get both or get none"). Deadlock is avoided because there is no Hold and Wait
• The students are friends and will ask each other to give up a held resource. Deadlock is avoided because pre-emption is allowed.

Livelock

Livelock is not deadlock-

Consider the following 'solution'

• The students will put down one held resource if they are unable to pick up the other resource within 10 seconds. This solution avoids deadlock however it may suffer from livelock.

Livelock occurs when a process continues to execute but is unable to make progress. In practice Livelock may occur because the programmer has taken steps to avoid deadlock. In the above example, in a busy system, the student will continually release the first resource because they are never able to obtain the second resource. The system is not deadlock (the student process is still executing) however it's not making any progress either.

Dining Philosophers

The Dining Philosophers problem is a classic synchronization problem. Imagine I invite N (let's say 5) philosophers to a meal. We will sit them at a table with 5 chopsticks (one between each philosopher). A philosopher alternates between wanting to eat or think. To eat the philosopher must pick up the two chopsticks either side of their position (the original problem required each philosopher to have two forks). However these chopsticks are shared with his neighbor.

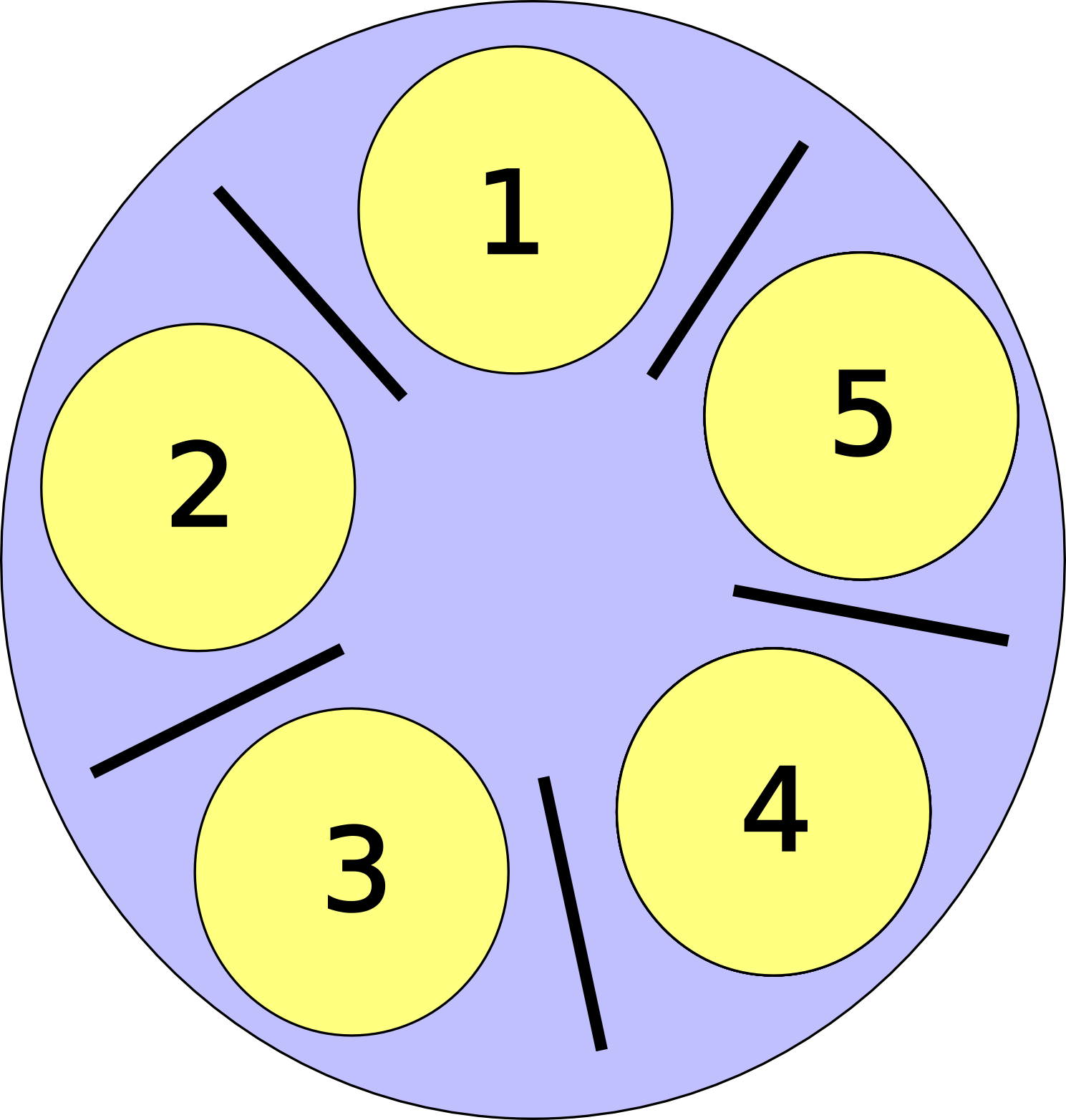
Is it possible to design an efficient solution such that all philosophers get to eat? Or, will some philosophers starve, never obtaining a second chopstick? Or will all of them deadlock? For example, imagine each guest picks up the chopstick on their left and then waits for the chopstick on their right to be free. Oops - our philosophers have deadlocked!