GCN, GAT - lshhhhh/deep-learning-study GitHub Wiki
- https://newsight.tistory.com/313 (GCN, GAT)
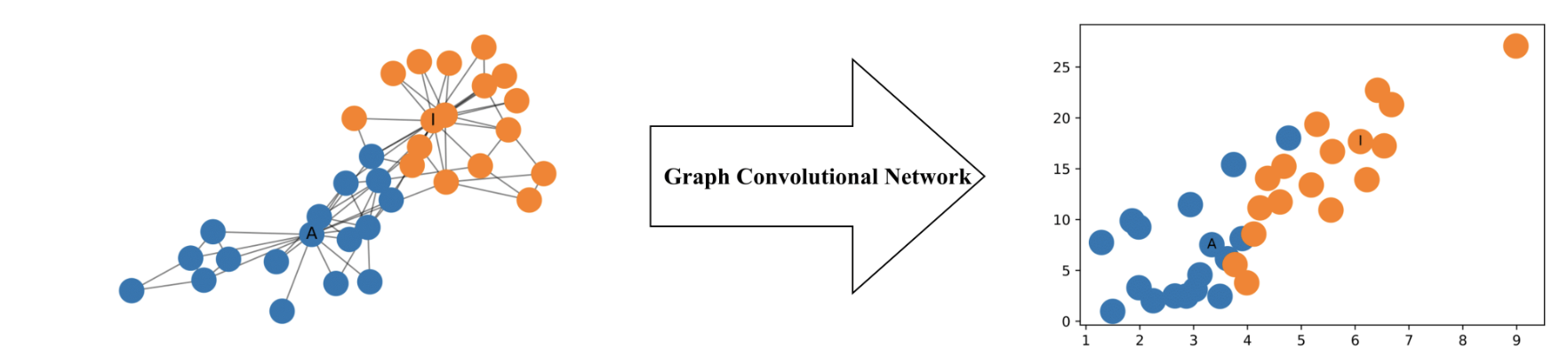 GCN을 사용하여 이렇게 2d 상에 network를 보존하며 올릴 수 있다. 심지어 위 예시에서는 아무런 학습 없이 변환 가능하였다.
GCN을 사용하여 이렇게 2d 상에 network를 보존하며 올릴 수 있다. 심지어 위 예시에서는 아무런 학습 없이 변환 가능하였다.
- Input X, A
- [N × F⁰] feature matrix, X
- N: node 수
- F⁰: 각 node의 input features 수
- [N × N] adjacency matrix of graph G, A
- [N × F⁰] feature matrix, X
- Hidden layer Hⁱ
- [N × Fⁱ] 각 row가 각 node의 feature representation인 feature matrix, Hⁱ
- Hⁱ = f(Hⁱ⁻¹, A)
- H⁰ = X
- f: propagation func. (아래에서 설명)
- 각 hidden layer에서 feature들은 propagation f를 사용하여 다음 layer의 feature들을 만들기 위해 aggregation된다. CNN에서 층을 쌓을 수록 local feature에서 점점 global feature로 올라가듯이 GCN 또한 전체 그래프에 대한 정보를 추출하게 된다. 여기서 핵심은 A를 곱하는 과정이 일종의 feature aggregation을 하는 과정인데, 이를 변형하면 GAT도 만들어낼 수 있다. (이것도 아래에서 설명)
- 이 framework를 기반으로 GCN의 variant들은 f만 달라진다.
아래는 제일 간단한 버전 중 하나다.
- f(Hⁱ, A) = σ(AHⁱWⁱ)
- Wⁱ: i번째 layer의 weight matrix, [Fⁱ × Fⁱ⁺¹]
- σ: a non-linear activation func. (ReLU)
- Adjacency matrix A를 곱해줌으로써, 이웃한 node의 값과 aggregation할 수 있다. (CNN과 유사, A가 identity func.이면 kernel_size=1(1x1) conv를 해준 것과 같다) 다만, A는 대각행렬의 성분이 모두 0(즉, 자기자신과의 연결이 없음)이라서 CNN의 filter에서 자기자신의 픽셀정보를 쓰지 않는 weight kernel이 생성되는 것과 같다. 따라서 identity matrix를 더해준 A^=A+I를 사용해서 문제를 해결한다.
Hⁱ[N×Fⁱ] = σ(A[N×N] * X[N×Fⁱ⁻¹] * Wⁱ[Fⁱ⁻¹×Fⁱ]
더 간단한 레벨로 가보자.
- i = 1 -> H1 = f(X, A)
- σ = the identity function
- 다음을 만족하는 W⁰: AH⁰W⁰ = AXW⁰ = AX 즉, f(X, A) = AX 인 propagation func.를 만들 수 있는데, 이 AX 값은 각 node에 대해 이웃 node들의 정보를 가져와 합한 결과라는 것을 알 수 있다.
단점부터 얘기하자면 GAT는 매우 느리다. 일단 간단하게만 적어두겠음.
기존의 GCN에서 A가 가진 binary값을 있는 그대로 사용하지 않고, 스스로 어떤 edge를 얼마나(실수값) 사용할지 결정할 수 있다. 이를 위해 masked-self multi-head attention을 도입한 것이 GATs이고, 이는 다음의 3가지 속성을 가진 (learnable/conditional/real-valued) Adjacency matrix를 만드는 것이 된다.