Алгоритм шифрования bmp на java заглушке - lanit-tercom-school/grouplock GitHub Wiki

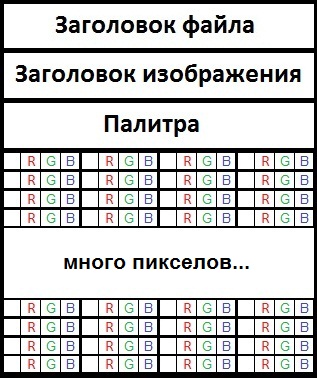
Прекрасно видно, что каждый пиксель в изображении кодируется 3 байтами, в которых содержится значение насыщенности R,G и B каналов (0-255). Чтоб зашифровать изображение, необходимо изменить эти значения.

1. Задаем n — количество чисел в ключе, по которому будем шифровать. ([k1,k2,k3,...kn])
2. Генерируем эти числа, которые будут принимать значения в диапазоне от 0 до 255, и заносим в массив key, размером n.
3. BMP-файл переводим в целочисленный массив srcPixels, каждый элемент которого содержит информацию о цвете соответствующего ему пикселя, т.е. этот массив будет длиной bitmap.height() * bitmap.width()
4. RGB компоненты i-го элемента массива srcPixels меняем следующим образом: R = (R + key[i % (key.length - 3)]) % 256, G = (G + key[i % (key.length - 3) + 1]) % 256, B = (B + key[i % (key.length - 3) + 2]) % 256
5. Из, уже измененного, массива srcPixels создаем новое изображение, которое и будет являться зашифрованным.
6. Генерируем QR-код, в котором записаны элементы массивa key.

1. Парсим QR-код и воспроизводим массив key.
2. Повторяем пункт (2) из алгоритма шифрования, но уже к зашифрованному файлу.
3. RGB компоненты i-го элемента массива srcPixels меняем следующим образом: R = (R - key[i % (key.length - 3)] + 256) % 256, G = (G - key[i % (key.length - 3) + 1] + 256) % 256, B = (B - key[i % (key.length - 3) + 2] + 256) % 256
4. Из измененного массива srcPixels создаем новое изображение, которое и будет являться расшифрованным.

При n=40:

Сгенерированный ключ:

014135065011031120213098090225235002159164069053046054089221166018143252176014191220128248108194211155076048237028002186

QR-код, содержащий ключ:

Изначальное изображение:

Зашифрованное изображение:

Вышеприведённый алгоритм "шифрования", как можно видеть, имеет заметный визуальный недостаток: зашифрованное изображение мало похоже на шум. Это связано с тем, что мы повторно используем ключ шифрования на RGB-компонентах картинки (то самое i % (key.length-3) в качестве индекса элемента ключа). То есть, например, ключ длины 40 (т. е. состоящий из 40 чисел 0–255) "покрывает" всего около 13 пикселей.

Если мы расширим ключ с помощью генератора псевдослучайных чисел (т. е. детерминированного алгоритма) до таких размеров, чтобы он покрывал изображение целиком, полученная на выходе картинка будет куда сильнее напоминать белый шум.

Рассмотрим алгоритм расширения ключа на пседокоде:

function generateExpansion(element: UInt8, expandingFactor: Int) returns Array<UInt8> {

    var lcg = new LinearCongruentialGenerator(seed: element)
    var expansion = new Array<UInt8>(length: expandingFactor)
            
    for i in 0 ..< expandingFactor {
        expinsion[i] = lcg.random() * 255
    }
            
    return expansion
}

function expand(key: Array<UInt8>, image: Image) returns Array<UInt8> {

    var numberOfBytes = image.height * image.bytesPerRow
    var expandingFactor = numberOfBytes / key.length + 1       

    var expandedKey = new Array<Array<UInt8>>(length: key.length)
    
    for i in 0 ..< expandedKey.length {
        expandedKey[i] = generateExpansion(element: key[i], expandingFactor: expandingFactor)
    }

    return expandedKey.flattened()
}

Функция generateExpansion принимает число 0–255 и коэффициент расширения, а возвращает массив из псевдослучайных чисел, сгегенированных с помощью зерна, равного этому числу. Длина этого массива совпадает с коэффициентом расширения. Для генерации используется линейный конгруэтный генератор (будет описан далее).

Функция expand рассчитывает коэффициент расширения исходя из размера ключа и числа байтов в битмапе по формуле numberOfBytes / key.length + 1. Единица прибавляется для того, чтобы длина расширенного ключа точно получилась не меньше количества байтов в битмапе.

Далее мы создаём двумерый массив exandedKey и заполняем его результатами вызовов функции generateExpansion для каждого значения исхоного ключа, и после всего преобразовываем этот массив в одномерный с помощью метода flattened и возвращаем.

Теперь посмотрим на генератор псевдослучайных чисел, который мы используем в функции generateExpansion . Он работает очень просто:

class LinearCongruentialGenerator {

    private var _seed: Double

    private const m = 139968.0
    private const a = 3877.0
    private const c = 29573.0

    function random() returns Double {
        _seed = (_seed * a + c) % m
        return _seed / m
    }

    // Конструктор
    LinearCongruentialGenerator(seed: Double) {
        _seed = seed
    }
}

Объект класса LinearCongruentialGenerator создаётся единожды для каждого элемента исходного ключа, а элементы расширенного ключа получаются многократным вызовом метода random на созданном объекте. Метод random возвращает псевдослучайное дробное число в диапазоне 0–1. Константы m, a, c фиксированы. Их значения подобраны так, чтобы последовательность чисел, генерируемых с каждым вызовом random, была похожа на случайную (см. статью в Википедии)

Возьмём картинку:

И применим к ней наш алгоритм:

Гораздо лучше, но всё ещё не то: однородный фон преобразуется в чёрно-белый шум, а неоднородный передний план — в цветной. Это легко исправить. Заведём фиксированные константы:

const redOffset = 234
const greenOffset = -132
const blueOffset = 17

Подправим формулы шифрования:

R = (R + key[i % (key.length-3)    ] + 512 + redOffset) % 256
G = (G + key[i % (key.length-3) + 1] + 512 + greenOffset) % 256
B = (B + key[i % (key.length-3) + 2] + 512 + blueOffset) % 256

И дешифрования:

R = (R - key[i % (key.length-3)    ] + 512 - redOffset) % 256
G = (G - key[i % (key.length-3) + 1] + 512 - greenOffset) % 256
B = (B - key[i % (key.length-3) + 2] + 512 - blueOffset) % 256

Применив алгоритм к тому же изображению, получим: